快速排序
一个非常有效的排序方法,正如其名,“快速排序”。平均时间复杂度是O(nlogn),最差时间复杂度为O(n^2),最优时间复杂度为O(nlogn)。
这里记录一下快排中遇到的一些难理解的地方。
I)循环开始方向。
如果“基准数”选择的是每次队列的最左边数字,那么此时我们应该从最右边开始循环。相反,如果我们选取的是最右边的数,那么我们就应该从最左边开始循环。道理我们分析一下就可以很明朗。
例如初始序列为3 1 2 4 5这样的一个数列要从小到大排列,如果我们选择最左边的数字为基准数开始模拟
3 1 2 4 5
i-> <-j
3 1 2 4 5
i-> <-j
3 1 2 4 5
i-> <-j
3 1 2 4 5
i-> j
3 1 2 4 5
ij
可以看到,ij相遇的时候就是基准数将要去到的位置,更准确的说就是全部排序之后基准数应该在的位置。这里我们举例分析为什么循环开始方向一定要和基准数所在的位置相反。
如上例,若循环开始由i开始,那么最终的结果有两种
1)最终以i遇到j为终止标志
寻找的过程应该是i j i j ... i j i。我们分析最后三步,当倒数第三次寻找结束的时候,i应该找到的是比基准数要大的数,倒数第二次j则是要寻找比基准数要小的数,当上述这两次寻找结束之后我们要做的是互换ij所找的数的位置,这时候i位置的是比基准小的数,而j位置的是比基准大的数。接着进行最后一步,这时的情况就是我们说的i遇到j结束,但是此时j位置的数字是比基准数大的,交换之后出错。下面我们模拟
3 1 2 4 0 5
i-> <-j
3 1 2 4 0 5
i-> <-j
3 1 2 4 0 5
i-> <-j
3 1 2 4 0 5
i j
3 1 2 0 4 5
i j
3 1 2 0 4 5
i-> j
3 1 2 0 4 5
ij
4 1 2 0 3 5
ij
2)最终以j遇到i为终止标志
分析同上,这种情况会更简单,i最后停下的数字为比基准数大的数字,此时j遇到i停下来就是这个比基准数要大的数字。模拟
3 1 2 4 5
i-> <-j
3 1 2 4 5
i-> <-j
3 1 2 4 5
i-> <-j
3 1 2 4 5
i-> j
3 1 2 4 5
ij
4 1 2 3 5
ij
由此可见,如果循环方向与基准数所在方向相同的话最后找到的数一定是比基准数要大的数,所以我们必须让循环方向与基准数所在的方向相反。
II)时间复杂度
先贴上手写的快排代码
1 void quicksort(int *a,int left,int right){ 2 int temp,index,i,j; 3 i=left; 4 j=right; 5 index=a[left]; 6 if(left>right) return ; 7 while(i!=j){ 8 while(a[j]>=index&&j>i){ 9 j--; 10 } 11 while(a[i]<=index&&j>i){ 12 i++; 13 } 14 if(i<j){ 15 temp=a[i]; 16 a[i]=a[j]; 17 a[j]=temp; 18 } 19 } 20 a[left]=a[i]; 21 a[i]=index; 22 quicksort(a,left,i-1); 23 quicksort(a,i+1,right); 24 }
可以看到手写快排里面使用的递归的算法,我们把它和二叉树做类比。你会发现非常有意思的地方,快排其实就是把数组中的所有数字用中序遍历的方式放到一颗二叉树中,每一个基准数在树中就是父结点,每次递归不断的添加字结点(即下层的父结点),直到子结点为空,然后用先序遍历的顺序来存储数组。
例如无序数列:5 1 9 3 7 4 8 6 2,那么这个数列的递归过程可以总结成下图(画图太麻烦了,我就直接用手画了=w=)
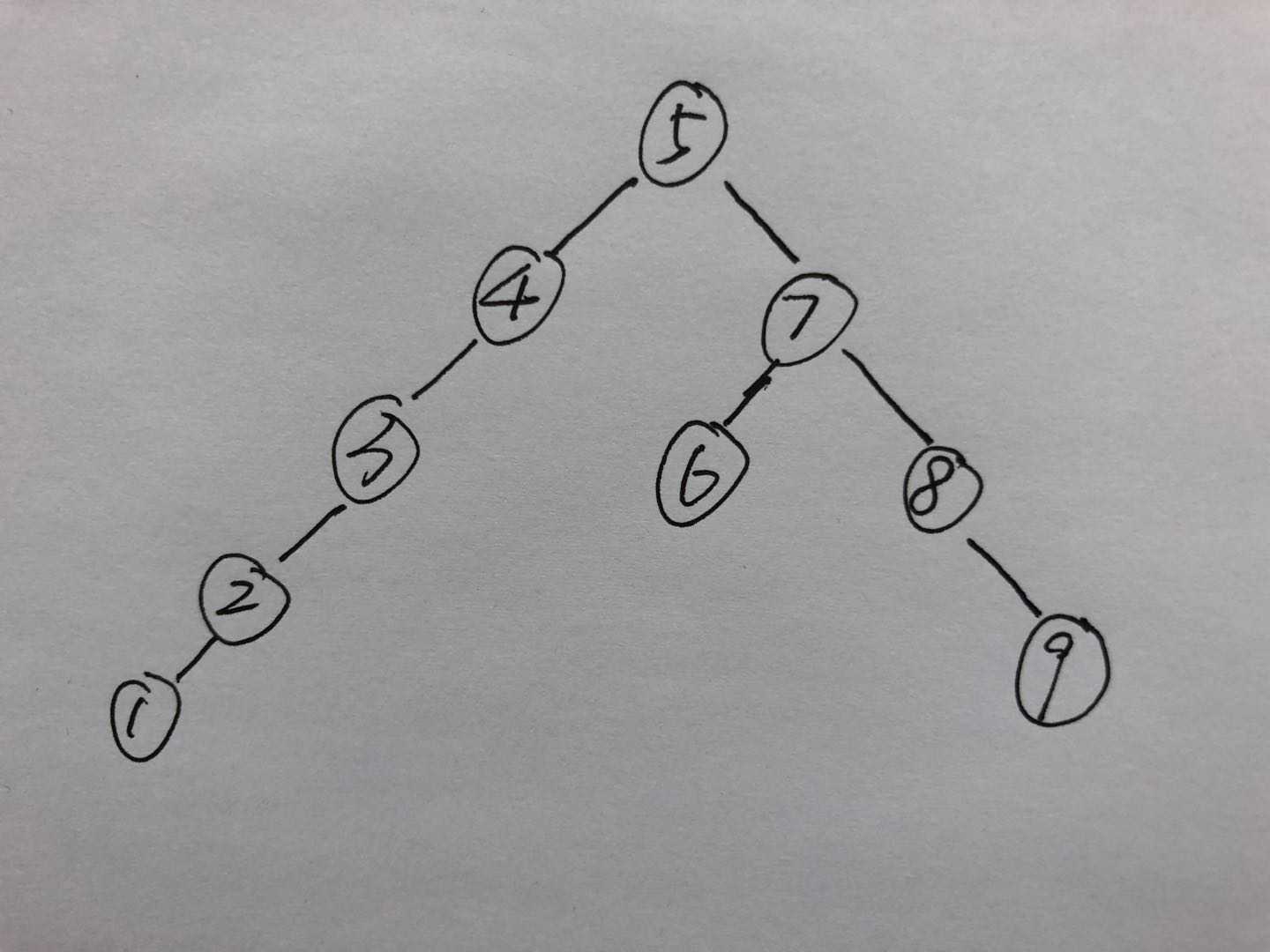
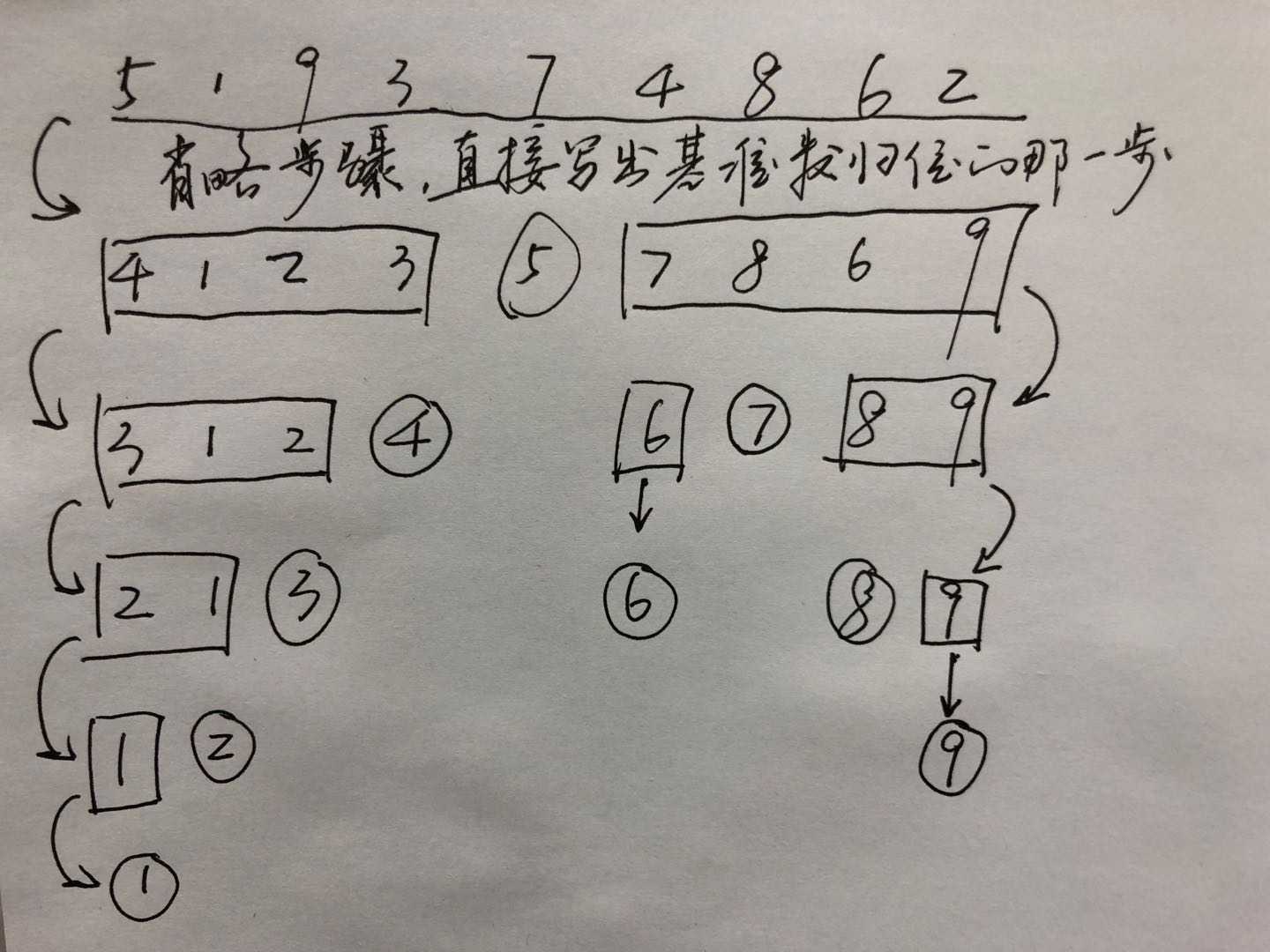
可以看到如果每次的分区都划分很均匀的话,那么我们可以得到
1)最优时间复杂度。设最优情况的时间复杂度为T(n),则有T(n)=2T(n/2)+n=4T(n/4)+2n=...=nT(1)+logn*n即为O(nlogn)。,
2)最坏时间复杂度。同理,最坏情况为正序或者反序,正序是\形状的二叉树,反序则是/形状的二叉树,二者的时间复杂度T(n)=n-1+n-2+...+1=n(n-1)/2=O(n^2)。
3)平均复杂度。这个确实有点难算,暂时鸽了,等加强一下概率论的知识再来补全。
