题目：有N条直线，最多可以形成几个交点？（用递归方法）
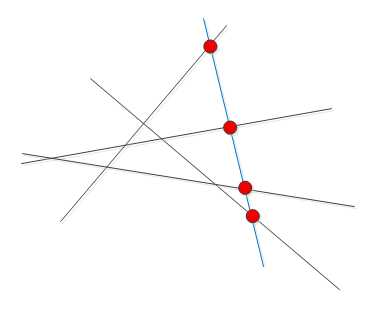
贪婪法：假如4个黑线有多少焦点是知道的，那第五条线最多能加4个，n条线，？？？？
2.2循环改为递归
阶乘，废布垃圾数列
列题：从1到100（不能用for...while...）
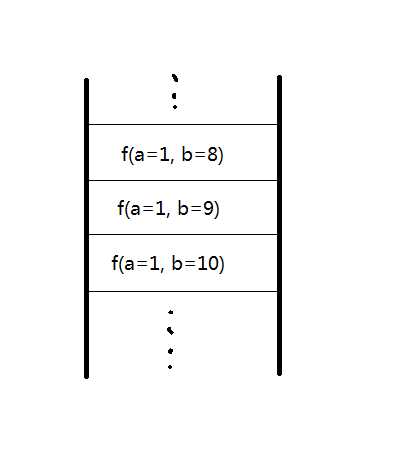
第十行，从a打印到b，到最后，a=b，则就就打印出来了。
和栈有关，压栈（容易导致栈溢出：）：保存当前函数执行的参数，每调用一次就保存一次，a和b
1.着相似性，2 找出口
题目（2）
求串的翻转串：
递归之后，只剩下一个，则返回自身。
题目三
[2.5 真题 振兴中华]
小明参加了学校的趣味运动会，其中的一个项目是：跳格子。 地上画着一些格子，每个格子里写一个字，如下所示：（也可参见下图） 从我做起振 我做起振兴 做起振兴中 起振兴中华 比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。 要求跳过的路线刚好构成“从我做起振兴中华”这句话。 请你帮助小明算一算他一共有多少种可能的跳跃路线呢？
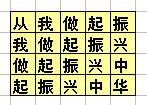
答案：35
解决方法：
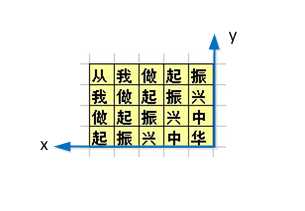加上坐标：华：（1，1），从（5，4）
加上坐标：华：（1，1），从（5，4）即从（5，4）走到（1，1）共有多少走法
递归主要是出口：当走到最下一行（最后一列）就不能再走
-------------------------------------------------------------------------------------------------------------------------------------
[2.6 真题 出栈顺序]
X星球特别讲究秩序，所有道路都是单行线。 一个甲壳虫车队，共16辆车，按照编号先后发车，夹在其它车流中，缓缓前行。 路边有个死胡同，只能容一辆车通过，是临时的检查站，如图所示。 X星球太死板，要求每辆路过的车必须进入检查站，也可能不检查就放行，也可能仔细检查。 如果车辆进入检查站和离开的次序可以任意交错。那么，该车队再次上路后，可能的次序有多少种？ 为了方便起见，假设检查站可容纳任意数量的汽车。 显然，如果车队只有1辆车，可能次序1种；2辆车可能次序2种；3辆车可能次序5种。
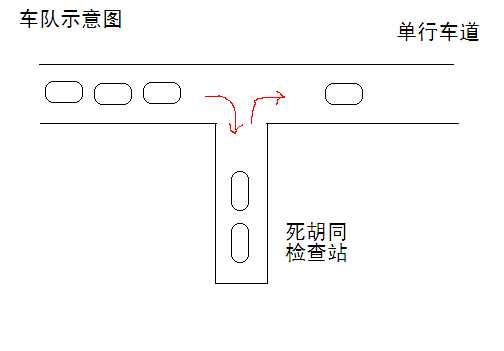
解决方法：
------------------------------------
题目：
[2.7 真题 趣味算式填符号]
匪警请拨110,即使手机欠费也可拨通！ 为了保障社会秩序，保护人民群众生命财产安全，警察叔叔需要与罪犯斗智斗勇，因而需要经常性地进行体力训练和智力训练！ 某批警察叔叔正在进行智力训练： 1 2 3 4 5 6 7 8 9 = 110 请看上边的算式，为了使等式成立，需要在数字间填入加号或者减号（可以不填，但不能填入其它符号）。之间没有填入符号的数字组合成一个数，例如：12+34+56+7-8+9 就是一种合格的填法；123+4+5+67-89 是另一个可能的答案。 请你利用计算机的优势，帮助警察叔叔快速找到所有答案。 每个答案占一行。形如： 12+34+56+7-8+9 123+4+5+67-89 ......
解决方法：
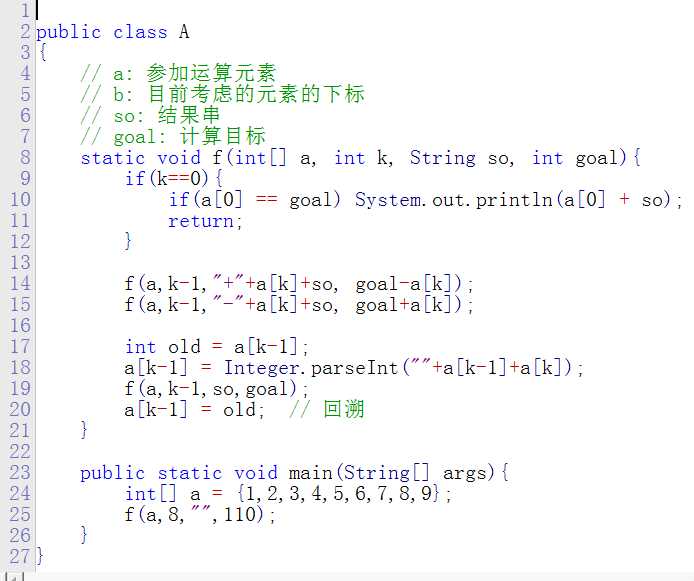
参数的设计是关键
----------------------
题目：
[2.8 真题 39级台阶]
、
小明刚刚看完电影《第39级台阶》。离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级! 站在台阶前，他突然又想着一个问题： 如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？ 请你利用计算机的优势，帮助小明寻找答案。
提示：间接递归...A调B...B又调A...两个函数互相调用实现？？？？？？？？？？（自己想）
作业题目：
[2.9 作业]
1
公园票价为5角。假设每位游客只持有两种币值的货币：5角、1元。
再假设持有5角的有m人，持有1元的有n人。 由于特殊情况，开始的时候，售票员没有零钱可找。 我们想知道这m+n名游客以什么样的顺序购票则可以顺利完成购票过程。 显然，m < n的时候，无论如何都不能完成； m>=n的时候，有些情况也不行。比如，第一个购票的乘客就持有1元。 请计算出这m+n名游客所有可能顺利完成购票的不同情况的组合数目。 注意：只关心5角和1元交替出现的次序的不同排列，持有同样币值的两名游客交换位置并不算做一种新的情况来计数。
给出2中解法，（将最后一个人单独考虑；把第一个人单独考虑）
