标签:des style blog class code java
通俗的说就是:一组平面上的点,求一个包含所有点的最小凸多边形,这个最小凸多边形就是凸包。
概要:Graham算法的主要思想就是,最终形成的凸包,即包围所有点的凸多边形,假定多边形是按逆时针方向生成的,那么多边形内部包围的所有点与多边形每个有向边的关系都是:点在有向边的左边。依照此思想,只要找到一个出发点,然后依此出发点按逆时针方向构建多边形,并保证每加入一条有向边时,都要满足其余点都在该边的左边。
***点与线的关系
定义:平面上的三点P1(x1,y1),P2(x2,y2),P3(x3,y3)的面积量:
|x1 x2 x3|
S(P1,P2,P3) = |y1 y2 y3| = (x1-x3)*(y2-y3) -
(y1-y3)*(x2-x3)
|1 1 1
|
当P1P2P3逆时针时S为正的,当P1P2P3顺时针时S为负的。
令矢量的起点为A,终点为B,判断的点为C,
如果S(A,B,C)为正数,则C在矢量AB的左侧;
如果S(A,B,C)为负数,则C在矢量AB的右侧;
如果S(A,B,C)为0,则C在直线AB上。
具体算法过程:
(1)输入:点集S={P}
(2)寻找基点P0:在所有点中找到y坐标最小的点,若找到多个,则选取其中X坐标最大的点作为基点,若只找到一个,则直接以这个点作为基点。
(3)排序:以基点为起点,以其余点为终点构成一个向量<P0,PK>,逐个计算每个向量与x轴正方向的夹角,并按夹角有小到大进行排序,得到一个排序的点S1={p0,p1,p2,p3…p(N-1)};对于夹角相同的点,剔除掉离基点近的点,只保留离基点最远的那个点。
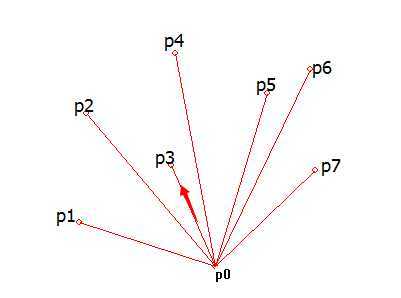
注意:由于计算角度复杂且耗时,在这里采用另外一种方式处理,根据上面的点线关系,从基点p0出发,依次遍历其它点,设为pk,p0和pk就构成一条有向向量,依次判断其它点(如pm)在向量的哪个方向,若在线段右边,则用其它点代替pk,构成一个新向量p0pm,继续判断剩余的点,这样一趟下来,就能找到最右边的点;依此道理判断其他点。如图:从向量p0p3(p3是任意选的,最终要将除p0外的所有点选到即可)开始,p1在向量p0p3左边,不变;p2在p0p3左边,向量不变;p4在p0p3右边,这时要将比较的向量变为p0p4;继续遍历p5,p5在p0p4右边,向量变为p0p5;继续遍历p6,p6在向量p0p5右边,向量变为p0p6;遍历p7,p7在向量p0p6右边,向量变为p0p7,这一趟下来就将p7这一个最右边的点找到了。同样的方法排序其他点,最后向量按与x轴正方向的顺序就是{p7,p6,p5,p4,p3,p2,p1},依次递增。
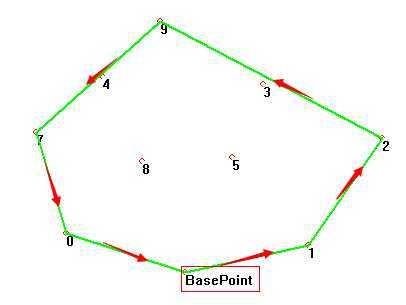
(4)构造凸包:
第一步:首先将基点p0入栈,p1和p2也依次入栈;
第二步:取栈顶的前两个点构成向量,即向量<p(k-1),pk>;
第三步:判断点p(k+1)是否在向量的左边;
第四步:
情况1:若在向量的左边,则将点p(k+1)入栈,重复第二步;
情况2:若在向量的右边,将点pk出栈,继续取下一个点,重复步骤二。
第五步:最后栈中存储的点就为凸包。
1、判断点p3是否在p1p2左边函数。(注意计算机屏幕坐标系与数学直角坐标系,y轴方向相反)
1 int CMyMath::Isleft(Cpoint2D p1,Cpoint2D p2,Cpoint2D p3) 2 { 3 int s; 4 s = (p1.x-p3.x)*(p2.y-p3.y)-(p1.y-p3.y)*(p2.x-p3.x); 5 if (s<0) 6 { 7 return 1; //点在直线左侧(对屏幕坐标系) 8 } 9 else if (s>0) 10 { 11 return 2;//点在直线右侧 12 } 13 else 14 { 15 return 0;//点在直线上 16 } 17 }
2、定义一个点类
1 class Cpoint2D 2 { 3 public: 4 Cpoint2D(); 5 Cpoint2D(int x,int y); 6 virtual ~Cpoint2D(); 7 public: 8 int id; 9 int x,y; 10 };
3、定义一个CGramhamCaclu类,用来生成凸包
1 class CGramhamCaclu 2 { 3 public: 4 CGramhamCaclu(); 5 CGramhamCaclu(CGramhamCaclu& crah); 6 virtual ~CGramhamCaclu(); 7 public: 8 CArray<Cpoint2D,Cpoint2D> InitialPoints;//保存最初点的集合 9 CArray<Cpoint2D,Cpoint2D> SortPoints; //保存排序后的点的集合 10 CArray<Cpoint2D,Cpoint2D> temparr;//用来起栈的作用,保存凸包中的点 11 int top1,top2;//栈顶前两项索引 12 int index; //基点的索引 13 public: 14 void DrawPoints(CDC* pDC);//画原始点 15 void DrawMinmumPolygon(CDC*pDC);//画凸包 16 void CaculTuBao();//计算凸包 17 protected: 18 void InitialSortPoints(); 19 int FindBasePoint(CArray<Cpoint2D,Cpoint2D>& cp);//找基点 20 void Exchange(int index1,int index2); 21 bool Sort();//排序 22 void Stack();//构造凸包 23 };
4、CGramhamCaclu类详细代码

////////////////////////////////////////////////////////////////////// // Construction/Destruction ////////////////////////////////////////////////////////////////////// CGramhamCaclu::CGramhamCaclu() { } CGramhamCaclu::CGramhamCaclu(CGramhamCaclu& crah) { } CGramhamCaclu::~CGramhamCaclu() { } ///画原始点 void CGramhamCaclu::DrawPoints(CDC* pDC) { CPen * pen = new CPen(0,1,RGB(255,0,0)); CPen * oldpen = pDC->SelectObject(pen); int x,y; for (int i=0;i<InitialPoints.GetSize ();i++) { x = InitialPoints[i].x; y = InitialPoints[i].y; pDC->Ellipse(x-3,y-3,x+3,y+3);//画点 CString s; s.Format("%d",i); pDC->TextOut(x,y,s);//画序号 } pDC->SelectObject(oldpen); } //画凸包 void CGramhamCaclu::DrawMinmumPolygon(CDC* pDC) { CPen * pen = new CPen(0,1,RGB(255,0,0)); CPen * pen1 = new CPen(1,2,RGB(0,255,0)); int size = temparr.GetSize(); if (size>=3) { CPen * oldpen = pDC->SelectObject(pen); CString s("基点"); pDC->TextOut(InitialPoints[index].x,InitialPoints[index].y,s); //画每个点与基点构成的向量,可以不要 // for (int i1=1;i1<SortPoints.GetSize();i1++) // { // pDC->MoveTo(SortPoints[0].x,SortPoints[0].y); // pDC->LineTo(SortPoints[i1].x,SortPoints[i1].y); // } pDC->SelectObject(oldpen); CPen * oldpen1 = pDC->SelectObject(pen1); pDC->MoveTo(temparr[0].x,temparr[0].y); for ( int i=1;i<size;i++) { pDC->LineTo(temparr[i].x,temparr[i].y); } pDC->LineTo(temparr[0].x,temparr[0].y); pDC->SelectObject(oldpen1); } } //凸包计算 void CGramhamCaclu::CaculTuBao() { if (InitialPoints.GetSize()>=3) { InitialSortPoints();//初始化排序数组 CGramhamCaclu::index = FindBasePoint(SortPoints);//找基点 if (CGramhamCaclu::index>=0) { Exchange(CGramhamCaclu::index,0); bool sort = Sort(); //排序 if (sort) { Stack();//栈操作 } } } } //初始化排序数组 void CGramhamCaclu::InitialSortPoints() { if (InitialPoints.GetSize()>=3) { for (int i=0;i<InitialPoints.GetSize();i++) { SortPoints.Add (InitialPoints[i]); } } } //找基点 int CGramhamCaclu::FindBasePoint(CArray<Cpoint2D,Cpoint2D>& cp) { Cpoint2D cpd; int index =-1; CArray<int,int> carray; if (cp.GetSize()>=3) { index = 0; cpd = cp[0]; //找一个y最大值 for (int i=1;i<cp.GetSize();i++) { if (cpd.y<cp[i].y) { cpd = cp[i]; index = i; } } //找所有y最大值 for (int j=0;j<cp.GetSize();j++) { if (cp[j].y == cp[index].y) { carray.Add (j); } } //找x最大值 if (carray.GetSize()>1) { index = carray[0]; for (i=0;i<carray.GetSize();i++) { if (cp[index].x<cp[carray[i]].x) { index = carray[i]; } } } } return index; } //交换位置 void CGramhamCaclu::Exchange(int index1,int index2) { Cpoint2D temp; temp = SortPoints[index1]; SortPoints[index1] = SortPoints[index2]; SortPoints[index2] = temp; } //排序 bool CGramhamCaclu::Sort() { if (SortPoints.GetSize()<3) { return false; } Cpoint2D basePoint = SortPoints[0]; int isleft; for (int i=1;i<SortPoints.GetSize();i++) { for (int j=i+1;j<SortPoints.GetSize();j++) { isleft = CMyMath::Isleft(basePoint,SortPoints[i],SortPoints[j]); if (isleft==2) { Exchange(i,j); } } } return true; } //构造凸包 void CGramhamCaclu::Stack() { if (SortPoints.GetSize()>=3) { temparr.Add(SortPoints[0]); temparr.Add(SortPoints[1]); top1 = 1; top2 = 0; } int isleft; for (int i=2;i<SortPoints.GetSize();i++) { isleft = CMyMath::Isleft(temparr[top2],temparr[top1],SortPoints[i]); if (isleft==1) { temparr.Add(SortPoints[i]); top1++; top2++; } if (isleft==2) { temparr.RemoveAt(top1,1); top1--; top2--; i--; } } }
5、测试结果图
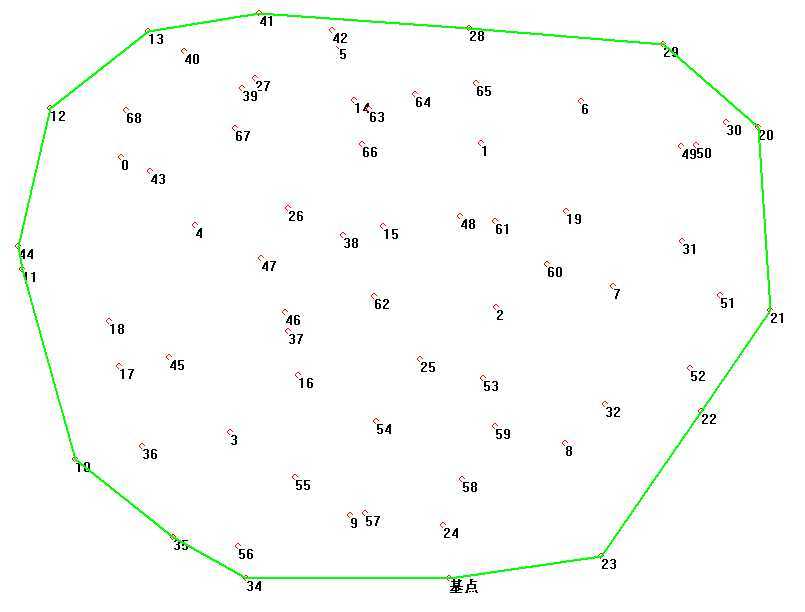
Graham算法—二维点集VC++实现,布布扣,bubuko.com
标签:des style blog class code java
原文地址:http://www.cnblogs.com/myboke/p/3722167.html