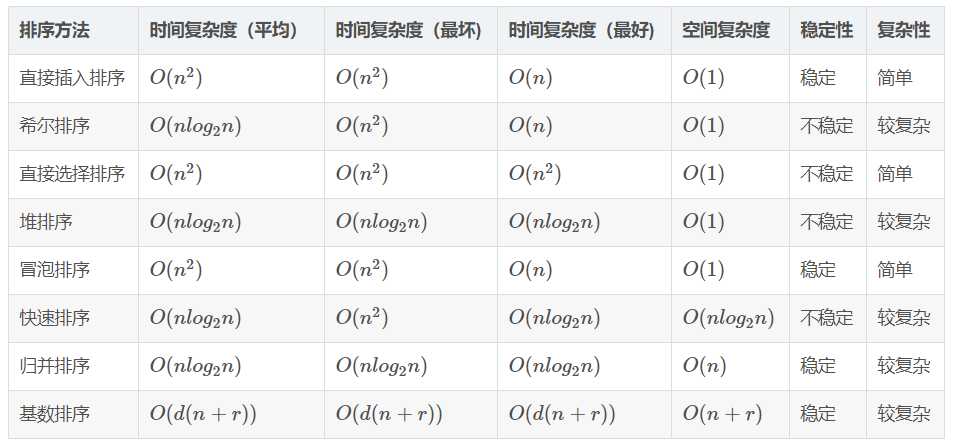
八大常用排序算法详细分析 包括复杂度:
排序有可以分为以下几类:
(1)、交换排序:冒泡排序、快速排序
(2)、选择排序:直接选择排序、堆排序
(3)、插入排序:直接插入排序、希尔排序
(4)、归并排序
(5)、基数排序(桶排序)
1.冒泡排序
顾名思义,冒泡排序就是用气泡从下往上冒的原理,将气泡(较小或较大的数)依次往前移。
具体做法(升序):设总共有N个元素,则至少需要进行N-1次冒泡。一次排序排序中,若前一个元素大于后一个元素,则交换两个元素,然后在依次判 断后面两两相邻元素大小并进行交换。进行完N-1轮冒泡后,排序完成。
C++算法实现:
void Bubble_Sort(int a[],int len)
{
int temp; //临时变量定义在循环之外,减少重复的定义 释放 ,提高效率
for (int i = 0; i < len-1 ; ++i)
{
for (int j = 0; j < len - i - 1; ++j)
{
if (a[j]>a[j + 1])
{
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
冒泡排序优化:
若某一次排序中没有数据进行交换,则排序完成,直接停止排序。所以代码可以优化。
void Select_Sort(int a[], int len)
{
int temp;
bool flag = true;
while (flag)
{
flag = false;
for (int i = 0; i < len - 1; ++i)
for (int j = i + 1; j < len; ++j)
if (a[i]>a[j])
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
flag =false;
}
}
}
2.直接选择排序
直接选择排序的原理比较简单,就是每一次从数列中选择一个最大(或最小)的元素,将其依次放入数组。
具体做法:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
C++算法实现:
void Select_Sort(int a[], int len)
{
int temp;
for (int i = 0; i < len - 1; ++i)
for (int j = i + 1; j < len; ++j)
if (a[i]>a[j])
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
3.直接插入排序
直接插入排序的基本思想是:从第二个元素开始,每一步把前面的元素排成一个有序的数列,然后把这个元素有序地插入到前面有序的数列中,直到全部数据插入完毕为止。
假设有一组N个元素无序序列 :
(1) 将这个序列的第一个元素视为一个有序序列;
(2) 依次把第2个到第N个元素, 插入到这个有序序列中;
C++算法实现:
void Insert_Sort(int a[],int len)
{
int temp;
for (int i = 1; i < len; ++i)
for (int j = i; j >= 0; --j)
{
if (a[j] >= a[j - 1])
break;
else
{
temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
}
}
}
上面这种插入排序还可以进行优化,上面的方法需要通过中间变量进行很多次的交换,我们可以先找到待插入元素应该插入的位置后,将该位置后的元素依次后移,在将待插入元素插入它应该在的位置上,这样就能减少很多的额外交换操作。
直接插入算法优化:
void Insert_Sort(int a[],int len) { //插入排序优化: int temp; int j; for (int i = 1; i < len;++i) { temp = a[i]; for (j = i; j >= 1 && temp < a[j - 1]; --j) a[j] = a[j - 1]; a[j] = temp; } }
4.希尔排序
希尔排序是一种插入排序算法,又称作缩小增量排序。是对直接插入排序算法的改进。
其基本思想是:先取一个小于n的整数作为第一个增量,把全部数据分成个组。所有距离为的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量重复上述的分组和排序,直至所取的增量,即所有记录放在同一组中进行直接插入排序为止。该方法实质上是一种分组插入方法。
C++算法实现:
void Shell_Sort(int a[], int len) { int d = len >> 1; //右移运算符比除法快 int temp; int i,j,k; while (d!=0) { for (i = 0; i < d; ++i) //分成d组 分别排序 2个数一组 在4个数一组 ... 最后合成一组 { for (j = i + d; j < len; j += d) //对第i组排序 { temp = a[j]; for (k = j; k >= i+ d &&temp < a[k - d]; k-=d) { a[k] = a[k - d]; } a[k] = temp; } } d /= 2;//将每组两两合并,再进行排序 } }
