关于KMP算法的认识

目前大二，大一时年自己纯属划水度过，身为一个学计算机的可能连一些没学的还要差。感觉自己不能在这样颓废下去了，是时候要努力一波了。

决定开始从算法开始补起。

大一数据结构在字符串匹配的时候曾讲过，当时对计算机还处于相当懵逼的状态，自然也就不会。前几天看算法题又一次看到了，决定把它补回来。

KMP算法

首先要先看 BF算法——最简单直观的模式匹配算法

如果用BF暴力匹配的思路

算法步骤：

1. 分别利用计数指针i , j  指示主串S和模式T中当前正待比较的字符位置pos,j初值为0；
2. • 如果当前字符匹配成功（即S[i] == P[j]），则i++，j++，继续匹配下一个字符；
   • 如果失配（即S[i]! = P[j]），令i = i -j+2，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。
3. 如果j > T.length,说明模式T中每个字符依次和主串S中的一个连续字符序列相等，则匹配成功，返回和模式T中第一个字符相等的字符在主串S中的序列号（i-T.length）;否则称匹配不成功，返回0；

4.  1 int Index_BF(SString S,SString T, int pos)
    2 {//返回模式T在主串S中第pos个字符第一次出现的位置，若不存在，则返回0.
    3     //其中T非空，0<=pos<=S.length
    4     i = pos; j = 0;//初始化
    5     while(i<S.length && j<=T.length)//两个字符串均为比较到串尾
    6     {
    7         if(S.ch[i]==T.ch[j]){++i;++j;}
    8         else{i=i-j+2; j=0; }        //指针后退重新开始
    9     }
   10     if(j>T.length) return i-T.length;//匹配成功
   11     else return 0;
   12 }

   该算法时间复杂度O(n*m)

Kmp算法

MP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。

首先对next 数组进行解释说明

void getNext(char * p, int * next)
{
    next[0] = -1;
    int i = 0, j = -1;

    while (i < strlen(p))
    {
        if (j == -1 || p[i] == p[j])
        {
            ++i;
            ++j;
            next[i] = j;
        }    
        else
            j = next[j];
    }
}

关于匹配问题

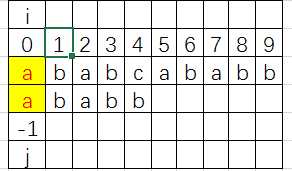
最初 i=0,j=-1; 满足算法语句     if (j == -1 || s[i] == p[j])  所以   i++;   j++;i=1;j=0;继续匹配，到下图

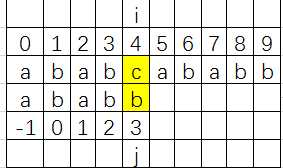
不满足判断语句    if (j == -1 || s[i] == p[j])  ，执行 else语句，  j = next[j];

算法流程：

int KmpSearch(char* s, char* p)  
{  
    int i = 0;  
    int j = 0;  
    int sLen = strlen(s);  
    int pLen = strlen(p);  
    while (i < sLen && j < pLen)  
    {  
        //①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++      
        if (j == -1 || s[i] == p[j])  
        {  
            i++;  
            j++;  
        }  
        else  
        {  
            //②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]      
            //next[j]即为j所对应的next值        
            j = next[j];  
        }  
    }  
    if (j == pLen)  
        return i - j;  
    else  
        return -1;  
}