今天的博客内容为常见排序算法,在写之前先描述一个特殊的概念:
排序算法稳定性:定义如下:
如果在元素序列中有两个元素R[i] 和R[j] ,他们的排序码 k[i] ==k[j] ,且在排序前,元素R[i] 在R[j] 前,如果在排序之后,元素R[i] 仍在R[j] 之前,则称这个排序算法是稳定的,否则称这个算法是不稳定的。
了解了排序算法稳定性的概念,接下来让我们开始真正了解,各大排序:
一. 插入排序
1.直接插入排序
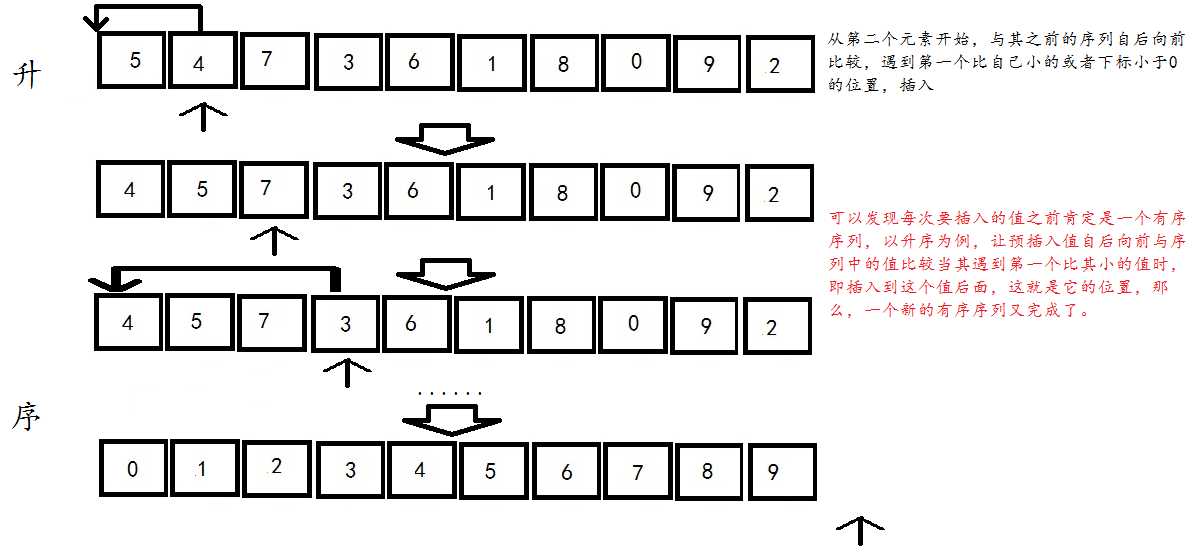
直接插入排序就是从第二个元素开始,按其排序码大小,每次取得元素都插入其之前的有序序列中,看下图例子:

1 void Insert_Sort_(DataType *array, int size) 2 { 3 //end==size的时候,说明此时已经插入完最后一个节点 再下去就越界 4 int i = 1; 5 //移值循环因子 6 int end = 0;; 7 DataType tmp = 0; 8 9 while (i < size) 10 { 11 tmp = array[i]; 12 end = i - 1; 13 //自后向前比,升序情况下,遇到大的就移位,遇到小的就退出循环 14 while ((end >= 0) && (array[end] > tmp)) 15 { 16 array[end + 1] = array[end]; 17 end--; 18 } 19 //注意循环出来前还end--了一下,所以要end+1。 20 array[end + 1] = tmp; 21 22 i++; 23 } 24 }
那么接下来就要讨论一个每每涉及排序都要讨论的话题——时间复杂度与空间复杂度:
直接插入排序:时间复杂度:最优:O(N) 最差:O(N^2) 最差情况:求一个降(升)序序列的升(降)序。
空间复杂度:O(1)
稳定与否? 稳定
适用场景:序列元素少,接近有序。
2.希尔排序
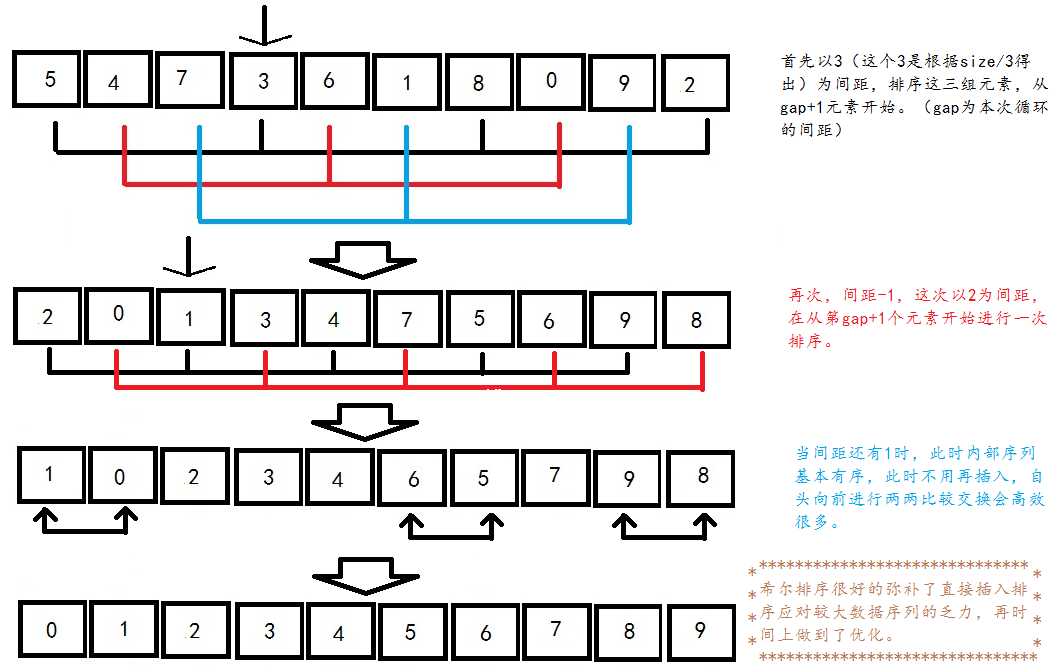
希尔排序,是对直接插入排序的优化,让插入排序更好地应对较大数据的无序序列:

1 void Shell_Sort_(DataType *array, int size) 2 { 3 int gap = size / 3 + 1; 4 //gap==1时候的比较因子 5 int Compare = 1; 6 int imov = gap; 7 //移值循环因子 自后向前 8 int end = 0; 9 10 //用于保存准插入值和需交换值 11 DataType tmp = 0; 12 13 while (gap != 1) 14 { 15 imov = gap; 16 while (imov < size) 17 { 18 tmp = array[imov]; 19 end = imov - gap; 20 //自后向前比,升序情况下,遇到大的就移位,遇到小的就退出循环 21 while ((end >= 0) && (array[end] > tmp)) 22 { 23 array[end + gap] = array[end]; 24 end-=gap; 25 } 26 //注意循环出来前还end-=gap了一下,所以要end+gap。 27 array[end + gap] = tmp; 28 29 imov++; 30 } 31 gap--; 32 } 33 }
希尔排序: 时间复杂度:O(N^1.3)
空间复杂度:O(1)
稳定与否? 不稳定
适用场景:序列元素较多,直接插入排序不合适。
二. 选择排序
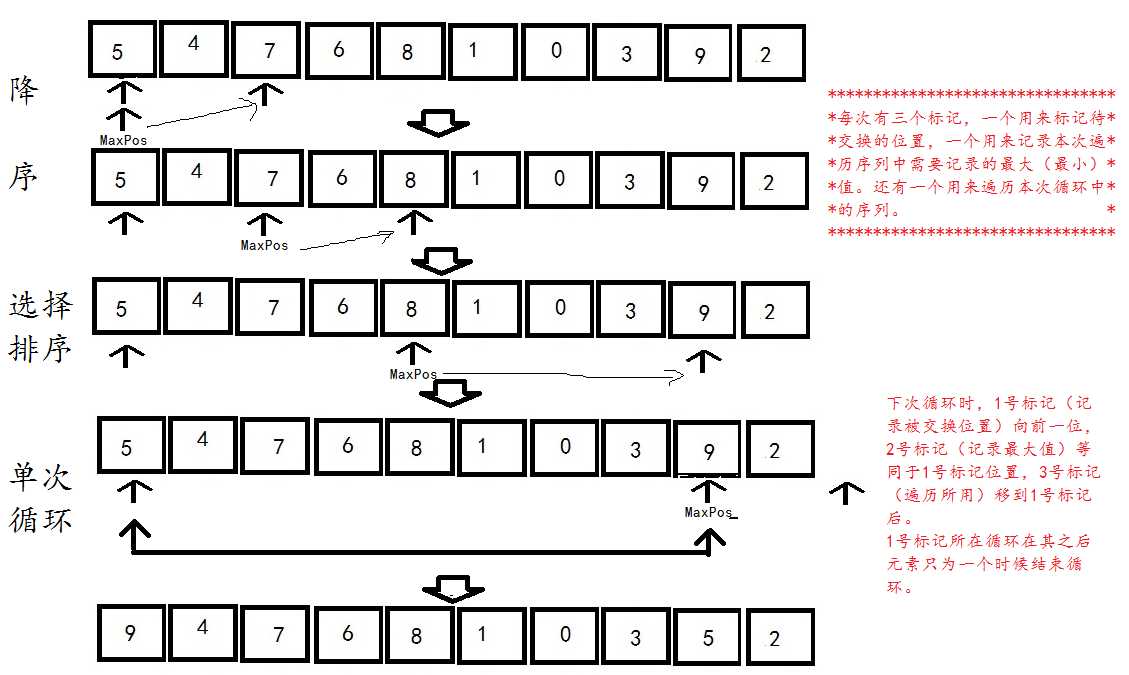
选择排序就是在一个存在N个元素的序列中,一共进行n-2趟遍历,第i趟(i=0,1,......,n-2)在后面n-i个待排序的数据元素集合中选出关键码最小的数据元素(升序为例),作为这个有序元素序列的第i个元素。

1 void Select_Sort_(DataType *array, int size) 2 { 3 int MaxPos = 0, i = 0, j = 0; 4 DataType tmp; 5 6 for (i = 0; i < size - 1; i++) 7 { 8 MaxPos = 0; 9 for (j = 0; j < size - i; j++) 10 { 11 if (array[MaxPos] < array[j]) 12 { 13 MaxPos = j; 14 } 15 } 16 if (MaxPos != size - i - 1) 17 { 18 tmp = array[MaxPos]; 19 array[MaxPos] = array[size - i - 1]; 20 array[size - i - 1] = tmp; 21 } 22 } 23 }
选择排序: 时间复杂度:O(N^2)
空间复杂度:O(1)
稳定与否? 不稳定
适用场景:无,类似堆排序。
三.快速排序
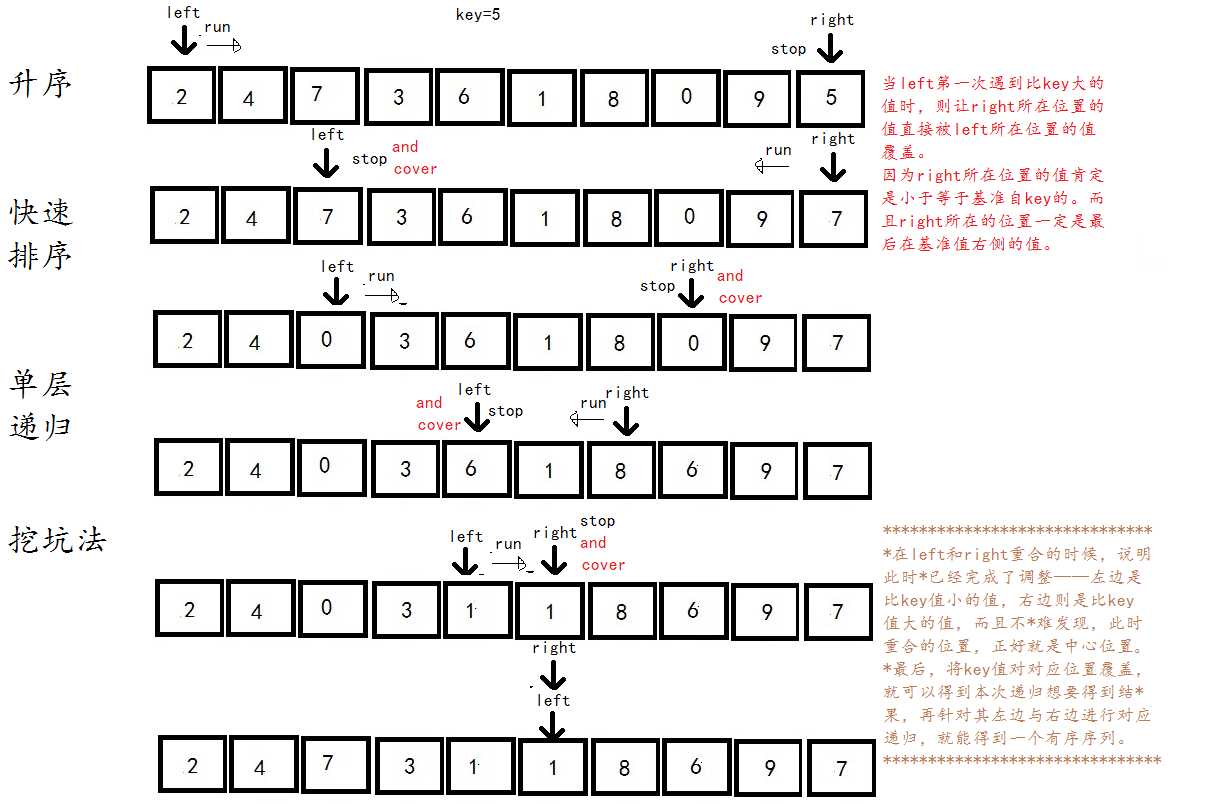
快速排序可以说是排序中最神奇而伟大的发明,其宗旨就是选择一个基准数,把比基准数大的数字放在其右边,比基准数小的数字放在左边,最后把基准数放在中间,形成递归,最后每个数左边的数字就是比其小的数字,每个数右边的数字就是比其大的数字,形成一个有序序列:

1 int partion_for_2(DataType* array, int left, int right) 2 { 3 DataType key = array[right - 1]; 4 int begin = left; 5 int end = right - 1; 6 7 while (begin < end) 8 { 9 while ((begin < end) && (array[begin] < key)) 10 begin++; 11 array[end] = array[begin]; 12 13 while ((begin < end) && (array[end] > key)) 14 end--; 15 array[begin] = array[end]; 16 } 17 if (begin != right - 1) 18 { 19 array[begin] = key; 20 } 21 return begin; 22 } 23 24 void Quick_Sort_2(DataType *array, int left, int right) 25 { 26 if (left < right) 27 { 28 int irt = partion_for_2(array, left, right); 29 Quick_Sort_2(array, left, irt); 30 Quick_Sort_2(array, irt + 1, right); 31 } 32 }
快速排序: 时间复杂度:最差O(N^2) 接近O(NlogN)
空间复杂度:O(1)
稳定与否? 不稳定
四.冒泡排序
冒泡排序可能是每个接触排序,或者说接触数据结构的人第一个接触到的排序算法。简而言之就是从前往后,两值交换,每次都能把本次遍历中最大的值放到本次序列的末尾,直到序列只剩下一个元素或更少时结束本次排序:
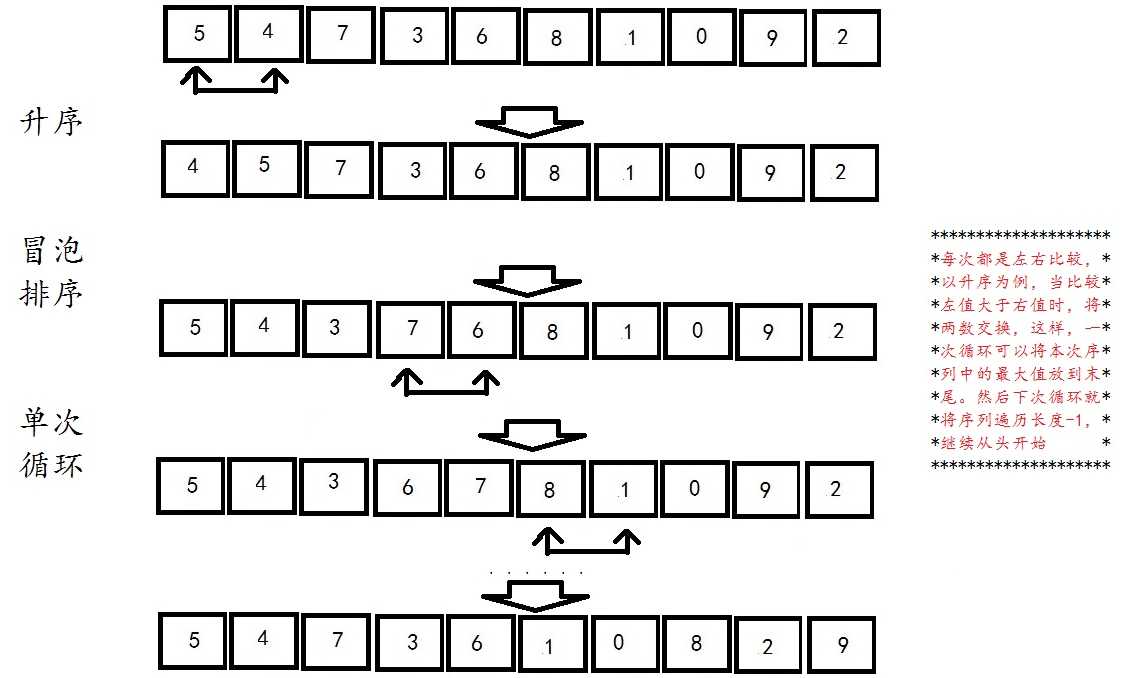
冒泡排序: 时间复杂度:最差:O(N^2) 最优:O(N)
空间复杂度:O(1)
稳定与否? 稳定
五.归并排序
归并排序即讲一组序列不断分割,分割到只有独立元素时再不断合并,形成有序序列,之后又不断合并,直到最上层的递归:
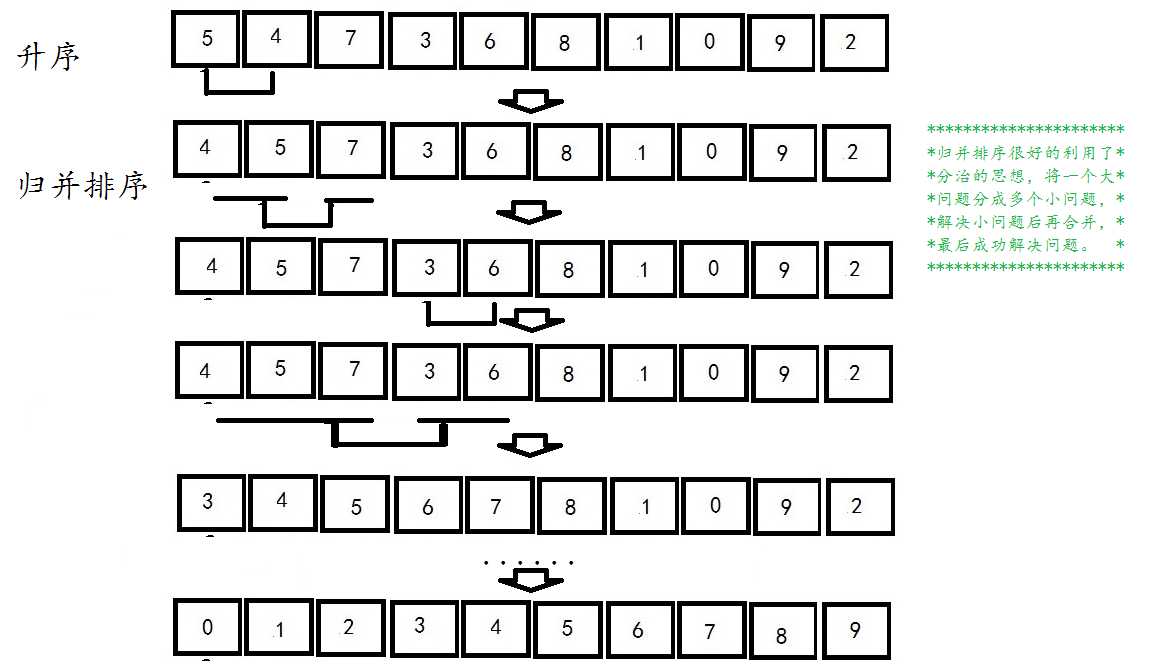

1 //合并 2 void _MergeData(DataType* array, int left, int right, int mid, DataType* tmp) 3 { 4 int l = left; 5 int r = mid + 1; 6 int i = 0; 7 while ((l <= mid) && (r <= right)) 8 { 9 if (array[l] <= array[r]) 10 { 11 tmp[i] = array[l]; 12 l++; 13 } 14 else 15 { 16 tmp[i] = array[r]; 17 r++; 18 } 19 i++; 20 } 21 while (l <= mid) 22 { 23 tmp[i] = array[l]; 24 i++; 25 l++; 26 } 27 while (r <= right) 28 { 29 tmp[i] = array[r]; 30 i++; 31 r++; 32 } 33 34 } 35 //分割 36 void _MergeSort(DataType*array, int left, int right) 37 { 38 if (left < right) 39 { 40 int mid = ((right - left) >> 1) + left; 41 DataType *tmp = (DataType*)malloc(sizeof(DataType)*(right - left + 1)); 42 //分左区域 43 _MergeSort(array, left, mid); 44 //分右区域 45 _MergeSort(array, mid + 1, right); 46 //合并 47 _MergeData(array, left, right, mid, tmp); 48 memcpy(array + left, tmp, sizeof(DataType)*(right - left + 1)); 49 free(tmp); 50 } 51 }
归并排序: 时间复杂度:O(NlogN)
空间复杂度:O(N)
稳定与否? 稳定
六.计数排序
计数排序是通过一次遍历,将一组数据阅览并保存在一组数组中,数组对应的位置为数值的大小,数组对应的位置的值为数值的个数。
以下为代码:

1 void CountSort(DataType *array, int size) 2 { 3 //1.确定区间 4 DataType MaxValue = array[0]; 5 DataType MinValue = array[0]; 6 7 for (int i = 0; i < size; i++) 8 { 9 if (array[i]>MaxValue) 10 MaxValue = array[i]; 11 if (array[i] < MinValue) 12 MinValue = array[i]; 13 } 14 15 //2.统计个数 16 int* ValueCount = (int*)calloc(MaxValue - MinValue + 1, sizeof(DataType)); 17 assert(ValueCount); 18 19 for (int i = 0; i < size; i++) 20 { 21 ValueCount[array[i] - MinValue]++; 22 } 23 24 //覆盖原数组 25 int begin = 0; 26 int end = MaxValue - MinValue; 27 int i = 0; 28 29 //3.从签到后开始遍历统计数组 30 while (begin <= end) 31 { 32 //为零则直接看数组下一个单元 33 if (ValueCount[begin] == 0) 34 { 35 begin++; 36 continue; 37 } 38 //如果不为零,那么说明此时的值为begin+MinValue 39 array[i] = begin + MinValue; 40 //调节索引因子们 41 ValueCount[begin]--; 42 i++; 43 } 44 }
计数排序: 时间复杂度:O(N*M)(N为数值数量,M为数值区间范围)
空间复杂度:O(N)
稳定与否? 不确定
七.基数排序
基数排序与计数排序不同,基数排序是根据多个排序码来多次排序数据,来得到最后的有序序列。我们下面以LSD为例:

1 //基数排序(低关键词排)--循环 2 void _RadixSortLSD(DataType*array,int size,DataType*Bucket,int bit) 3 { 4 int Radix = 1; 5 int Radix_Max = (int)pow((double)10, (double)bit); 6 7 while (Radix < Radix_Max) 8 { 9 int count[10] = { 0 }; 10 int StartArray[10] = { 0 }; 11 //1.统计个数 12 //计算一个位数的0~9出现的次数。 13 for (int i = 0; i < size; i++) 14 { 15 count[(array[i]/Radix) % 10]++; 16 } 17 //开始个数统计 确定各数字的区间 18 for (int i = 1; i < 10; i++) 19 { 20 StartArray[i] = StartArray[i - 1] + count[i - 1]; 21 } 22 23 //2.开始放置数据 24 for (int i = 0; i < size; i++) 25 { 26 int Value = (array[i] / Radix) % 10; 27 Bucket[StartArray[Value]++] = array[i]; 28 } 29 30 //3.回收数据 31 memcpy(array, Bucket, sizeof(DataType)*size); 32 Radix *= 10; 33 } 34 } 35 36 void RadixSortLSD(DataType *array, int size) 37 { 38 int bit = GetMaxRadix(array,size); 39 DataType* Bucket = (DataType*)malloc(sizeof(DataType)*size); 40 assert(Bucket); 41 42 _RadixSortLSD(array, size, Bucket,bit); 43 44 free(Bucket); 45 }
基数排序: 时间复杂度:O(N)(N为数值数量,M为数值区间范围)
空间复杂度:O(N)
稳定与否? 不稳定

