在计算机科学中,最长回文子串或最长对称因子问题是在一个字符串中查找一个最长连续子串,这个子串必须是回文。例如“banana”最长回文子串是“anana”。最长回文子串并不能保证是唯一的,例如,在字符串“abracadabra”,没有超过三的回文子串,但是有两个回文字串长度都是三,是“ada”和“aca”。在一些应用中需要返回全部的最长回文子串(所有字串都是回文,并且不能扩展为更大的回文子串)而不是返回其中之一或是最大的回文子串的长度。
[Manacher(1975)] 发现了一种线性时间算法,可以在列出给定字符串中从字符串头部开始的所有回文。并且,Apostolico, Breslauer & Galil (1995) 发现,同样的算法也可以在任意位置查找全部最大回文子串,并且时间复杂读是线性的。因此,他们提供了一种时间复杂度为线性的最长回文子串解法。替代性的线性时间解决 Jeuring (1994), Gusfield (1997)提供的,基于后缀树(suffix trees)。
很容易想到的一个解法是遍历所有的可能成为最长回文子串的字符串,从中挑选出最长的那个。这个解法可以通过遍历每一可能成为中心的字符开始向两边拓展,时间复杂度是O(n ^ 2)。下面介绍的Manacher算法可以在O(n)的时间复杂度完成最长回文子串的求解。
Manacher算法的核心是记录的当前向右拓展的最长回文的右边界,利用回文子串的对称性,对问题进行化简和转化。
首先Manacher算法为了消除奇偶性的影响,在原字符串中引入了一个在原串中不会出现的字符,用来将字符串长度的奇偶性影响给消除。
用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(包括S[i],也就是把该回文串“对折”以后的长度)。
S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
(p.s. 可以看出,P[i]-1正好是原字符串中回文串的总长度)
不妨记最右边界为right,其中心为id,则有:
if (P[2 * id - i] < right - i + 1) P[i] = P[2 * id - i]
else P[i] > P[2 * id - i]
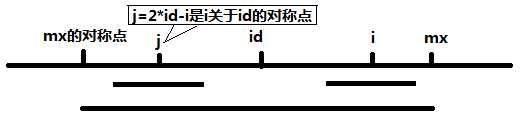
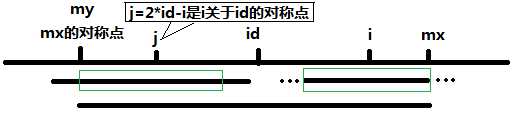
如果对称点的半径小于right - i + 1,那么i的半径和其相等,如果大于,那么还需要我们进行进一步的判断。
String manacher(String s) {
StringBuffer sb = new StringBuffer();
sb.append(‘#‘);
for (int i = 0; i < s.length(); i++) {
sb.append(s.charAt(i));
sb.append(‘#‘);
}
int[] m = new int[sb.length()];
m[0] = 1;
int id = 0;
int right = 0;
for (int i = 1; i < sb.length(); i++) {
m[i] = right > i ? Math.min(m[2 * id - i], right - i + 1) : 1;
while (i >= m[i] && (i + m[i]) <= sb.length() - 1 && sb.charAt(i - m[i]) == sb.charAt(i + m[i])) m[i]++;
if (i + m[i] - 1 > right) {
id = i;
right = m[i];
}
}
int maxR = m[0];
int index = 0;
for (int i = 0; i < m.length; i++) {
if (m[i] > maxR) {
maxR = m[i];
index = i;
}
}
String res = "";
for (int i = index - maxR + 1; i < index + maxR - 1; i++) {
if (sb.charAt(i) == ‘#‘) continue;
else res += sb.charAt(i);
}
return res;
}
