最近花了半个多月把Mchiael Nielsen所写的Neural Networks and Deep Learning这本书看了一遍,受益匪浅。
该书英文原版地址地址:http://neuralnetworksanddeeplearning.com/
回顾一下这本书主要讲的内容
1.使用神经网络识别手写数字
作者从感知器模型引申到S型神经元。然后再到神经网络的结构。并用一个三层神经网络结构来进行手写数字识别,
作者详细介绍了神经网络学习所使用到梯度下降法,由于当训练输入数量过大时,学习过程将变的时分缓慢,就引
入了随机梯度下降的算法用来加速学习。
选取二次代价函数

神经网络的权重偏置更新法则如下:
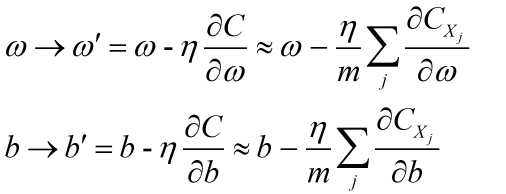
其中m是随机选取的m个训练样本,我们把这些随机训练样本标记为X1,X2,X3,..,Xm.。并把它们称为一个小批量数据。
2.反向传播算法如何工作
这一章作者主要介绍了反向传播的四个公式。并给出了反向传播算法的计算流程:
以MNIST数据集为例,包含50000幅用于训练的手写图片,10000幅用于校验的手写图片,10000幅用于测试的手写图片。
1.输入训练集样本的集合
2.初始化迭代期次数(epochs),开始循环 for i in range(epochs):
2.1 打算输入训练集样本,按mini_batch_size(小批量大小)划分成许多组
2.2 针对每一小批量数据应用随机梯度下降法,并更新权重和偏置(程序中update_mini_batch(self,mini_batch,eta)函数)
2.3 一轮训练结束,用测试数据集检验准确率
3.神经网络学习结束
其中2.2步骤,尤为重要,针对小批量数据(mini_batch),如何应用随机梯度下降法,更新网络参数(update_mini_batch)
1.输入小批量数据的集合 mini_batch
2遍历每一个实例 (x,y),开始循环 for x,y in mini_batch:
2.1计算每一个实例的梯度 (backprop(self,x,y)函数)
2.1.1 对每层l = 2,3,...,L,计算每一层带全权输入zl = wlal-1+bl,激活输出al = σ(zl)
2.1.2 计算输出层误差 δL=?C/?aL![]() σ‘(zL),计算?Cx/?ωL=δL(aL-1)T,?Cx/?bL=δL。(注意当选择不同的代价函数时δL值是不一样,
σ‘(zL),计算?Cx/?ωL=δL(aL-1)T,?Cx/?bL=δL。(注意当选择不同的代价函数时δL值是不一样,
当选择二次代价函数时,δL=(aL-y)![]() σ‘(zL),当选择交叉熵代价函数时,δL=(aL-y))
σ‘(zL),当选择交叉熵代价函数时,δL=(aL-y))
2.1.3 反向传播误差,对每个l = L-1,L-2,...,2 计算δl = ((ωl+1)Tδl+1)![]() σ‘(zl),计算?Cx/?ωl=δL(al-1)T,?Cx/?bl=δl
σ‘(zl),计算?Cx/?ωl=δL(al-1)T,?Cx/?bl=δl
2.1.4 ?Cx/?ω = [?Cx/?ω2,?Cx/?ω3,...,?Cx/?ωL], ?Cx/?b = [?Cx/?b2,?Cx/?b3,...,?Cx/?bL]
2.2计算梯度的累积和,Σ?Cx/?ω,Σ?Cx/?b
3.应用随机梯度下降法权重偏置更新法则更新权重和偏置 ω = ω-η/mΣ?Cx/?ω,b = b-η/mΣ?Cx/?b
选用三层神经网络,激活函数选取S型神经元,代价函数选取二次代价函数,实现程序如下
Network1.py:
# -*- coding: utf-8 -*- """ Created on Mon Mar 5 20:24:32 2018 @author: Administrator """ ‘‘‘ 书籍:神经网络与深度学习 第一章:利用梯度下降法训练神经网络算法 这里代价函数采用二次代价函数 ‘‘‘ import numpy as np import random ‘‘‘ 定义S型函数 当输入z是一个向量或者numpy数组时,numpy自动地按元素应用sigmod函数,即以向量形式 ‘‘‘ def sigmod(z): return 1.0/(1.0+np.exp(-z)) ‘‘‘ 定义S型函数的导数 ‘‘‘ def sigmod_prime(z): return sigmod(z)*(1-sigmod(z)) ‘‘‘ 定义一个Network类,用来表示一个神经网络 ‘‘‘ class Network(object): ‘‘‘ sizes:各层神经元的个数 weights:权重,随机初始化,服从(0,1)高斯分布 weights[i]:是一个连接着第i层和第i+1层神经元权重的numpy矩阵 i=0,1... biases:偏置,随机初始化,服从(0,1)高斯分布 biases[i]:是第i+1层神经元偏置向量 i=0,1.... ‘‘‘ def __init__(self,sizes): #计算神经网络的层数 self.num_layers = len(sizes) #每一层的神经元个数 self.sizes = sizes #随机初始化权重 第i层和i+1层之间的权重向量 self.weights = [np.random.randn(y,x) for x,y in zip(sizes[:-1],sizes[1:])] #随机初始化偏置 第i层的偏置向量 i=1...num_layers self.biases = [np.random.randn(y,1) for y in sizes[1:]] ‘‘‘ 前向反馈函数,对于网络给定一个输入向量a,返回对应的输出 ‘‘‘ def feedforward(self,a): for b,w in zip(self.biases,self.weights): #dot矩阵乘法 元素乘法使用* a = sigmod(np.dot(w,a) + b) return a ‘‘‘ 随机梯度下降算法:使用小批量训练样本来计算梯度(计算随机选取的小批量数据的梯度来估计整体的梯度) training_data:元素为(x,y)元祖的列表 (x,y):表示训练输入以及对应的输出类别 这里的输出类别是二值化后的10*1维向量 epochs:迭代期数量 即迭代次数 mini_batch:小批量数据的大小 eta:学习率 test_data:测试数据 元素为(x,y)元祖的列表 (x,y):表示训练输入以及对应的输出类别 这里的输出就是对应的实际数字 没有二值化 ‘‘‘ def SGD(self,training_data,epochs,mini_batch_size,eta,test_data=None): if test_data: #计算测试集样本个数 n_test = len(test_data) #计算训练集样本个数 n = len(training_data) #进行迭代 for j in range(epochs): #将训练集数据打乱,然后将它分成多个适当大小的小批量数据 random.shuffle(training_data) mini_batches = [training_data[k:k+mini_batch_size] for k in range(0,n,mini_batch_size)] #训练神经网络 for mini_batch in mini_batches: self.update_mini_batch(mini_batch,eta) #每一次迭代后 都评估一次对测试集数据进行预测的准确率 if test_data: print(‘Epoch {0}: {1}/{2}‘.format(j,self.evaluate(test_data),n_test)) else: print(‘Epoch {0} complete‘.format(j)) ‘‘‘ mini_batch:小批量数据 元素为(x,y)元祖的列表 (x,y) eta:学习率 对每一个mini_batch应用梯度下降,更新权重和偏置 ‘‘‘ def update_mini_batch(self,mini_batch,eta): #初始化为0 nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #依次对每一个样本求梯度,并求和 for x,y in mini_batch: #计算每一个样本代价函数的梯度(?Cx/?ω,?Cx/?b) delta_nabla_b,delta_nabla_w = self.backprop(x,y) #梯度分量求和 Σ?Cx/?ω nabla_b = [nb + dnb for nb,dnb in zip(nabla_b,delta_nabla_b)] #梯度分量求和 Σ?Cx/?b nabla_w = [nw + dnw for nw,dnw in zip(nabla_w,delta_nabla_w)] #更新权重 w = w - η/m*Σ?Cx/?ω self.weights = [w - (eta/len(mini_batch))*nw for w,nw in zip(self.weights,nabla_w)] #更新偏置 b = b - η/m*Σ?Cx/?b self.biases = [b - (eta/len(mini_batch))*nb for b,nb in zip(self.biases,nabla_b)] ‘‘‘ 计算给定一个样本二次代价函数的梯度 单独训练样本x的二次代价函数 C = 0.5||y - aL||^2 = 0.5∑(yj - ajL)^2 返回一个元组(nabla_b,nabla_w) = (?Cx/?ω,?Cx/?b) :和权重weights,偏置biases维数相同的numpy数组 ‘‘‘ def backprop(self,x,y): #初始化与self.baises,self.weights维数一样的两个数组 用于存放每个训练样本偏导数的累积和 nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #前向反馈 activation = x #保存除了输入层外所有层的σ(z)的值 activations = [x] #保存除了输入层外所有层的z的值 zs = [] #计算除了输入层外每一层z和σ(z)的值 for b,w in zip(self.biases,self.weights): z = np.dot(w,activation) + b zs.append(z) activation = sigmod(z) activations.append(activation) #计算输出层误差 delta = self.cost_derivative(activations[-1],y)*sigmod_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta,activations[-2].transpose())
#计算反向传播误差 for l in range(2,self.num_layers): z = zs[-l] sp = sigmod_prime(z) delta = np.dot(self.weights[-l+1].transpose(),delta)*sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta,activations[-l-1].transpose()) return (nabla_b,nabla_w) ‘‘‘ 对神经网络预测准确率进行评估 ‘‘‘ def evaluate(self,test_data): #np.argmax返回最大值所在的索引 这里获取预测数值和实际数值组成元组的列表 test_results = [(np.argmax(self.feedforward(x)),y) for x,y in test_data] #计算预测值 == 实际值的总个数 return sum(int(x==y) for x,y in test_results) ‘‘‘ 计算损失函数的偏导数?C/?a a是实际输出 ‘‘‘ def cost_derivative(self,output_activations,y): return (output_activations - y)
def network_baseline():
#遇到编码错误:参考链接http://blog.csdn.net/qq_41185868/article/details/79039604S
#traning_data:[(784*1,10*1),...],50000个元素
#validation_data[(784*1,1*1),....],10000个元素
#test_data[(784*1,1*1),....],10000个元素
training_data,validation_data,test_data = mnist_loader.load_data_wrapper()
print(‘训练集数据长度‘,len(training_data))
print(training_data[0][0].shape) #训练集每一个样本的特征维数 (784,1)
print(training_data[0][1].shape) #训练集每一个样本对应的输出维数 (10,1)
print(‘测试集数据长度‘,len(test_data))
print(test_data[0][0].shape) #测试机每一个样本的特征维数,1,1 (784,1)
#print(test_data[0][1].shape) #测试机每一个样本对应的输出维数 () 这里与训练集的输出略有不同,这里输出是一个数 并不是二指化后的10*1维向量
print(test_data[0][1]) #7
#测试
net = Network([784,30,10])
‘‘‘
print(net.num_layers) #3
print(net.sizes)
print(net.weights)
print(net.biases)
‘‘‘
net.SGD(training_data,30,10,3.0,test_data=test_data)
#运行程序
network_baseline()
