感知器算法是一种线性分类器(原始形式和对偶形式)
1.首先,我们假定线性方程 wx+b=0 是一个超平面,令 g(x)=wx+b,也就是超平面上的点x都满足g(x)=0。对于超平面的一侧的点满足:g(x)>0; 同样的,对于超平面另一侧的点满足:g(x)<0.
结论一:对于不在超平面上的点x,它到超平面的距离:
证明:如下图所示,O表示原点,Xp表示超平面上的一点,X是超平面外的一点,w是超平面的法向量。


等式1说明:向量的基本运算法则,OX=OXp+XpX. 因为w是法向量,所以w/||w||是垂直于超平面的单位向量。
等式2说明:将等式1带入g(x)=wx+b;由于Xp在超平面上,所以g(Xp)=w^T*Xp+w0 = 0
以上得证。
2.下面区分一下易混淆的两个概念,梯度下降和随机梯度下降:
梯度下降:一次将误分类集合中所有误分类点的梯度下降;----对偶形式
随机梯度下降:随机选取一个误分类点使其梯度下降。----原始形式
3.对于误分类的数据来说,当w*xi + b>0时,yi = -1,也就是,明明是正例,预测成负例。因此,误分类点到超平面的距离为:
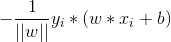
因此所有误分类点到超平面的总距离为:
忽略1/||w||,我们就可以得到感知机学习的损失函数。
损失函数:
这个损失函数就是感知机学习的经验风险函数。
下面我们计算损失函数的梯度:
值得我们注意的是,以上求和都是针对误分类集合M中的样本点进行的。对于正确分类的样本点,则不需要考虑。
下面我们就得到了我们的更新策略:
随机选取误分类点(xi,yi),对w,b进行更新:
4.感知器算法的原始形式:
输出w,b; 感知机模型f(x)=sign(w*x+b)
(1)选取初值w0,b0
(2)在训练集中选取数据(xi,yi)
(3)若yi*(w*xi+b)<=0, (该样本点被误分类了)
(4)转至(2),直至训练集中没有误分类点。
5感知器对偶形式:
基本思想:
将 w 和 b 表示为实例 xi 和标记 yi线性组合的形式,通过求解其系数而求得 w、b 。假设 w0,b0为0,对误分类点(xi,yi) 通过
w=w+ηyixi
b=b+ηyi
逐步修改 w,b ,设修改 n 次,则 w,b 关于(xi,yi) 的增量分别为 αiyixi 和 αiyi, 其中αi=niη ,则最后学习到的 w,b可以分别表示为
w=∑αiyixi
b=∑αiyi
这里,αi≥0,=1,2,?N, αi=niη ,ni 的意义是样本 i 被误分的次数,所以当 η=1 时,表示第 i 个样本由于被误分而更新的次数,实例点更新次数越多,表明它距离分离超平面越近,也就越难正确分类。
伪代码:

为了方便后期的计算,可先求出Gram(格拉姆矩阵)矩阵。
例如,正例:x1 = (3,3)^T, x2 = (4,3)^T, 负例: x3 = (1,1)^T
那么Gram(格拉姆矩阵)矩阵就是:
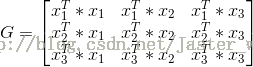

因为对偶形式中会大量用到xi*xj的值,所以提前求出Gram矩阵会方便很多。










