1.题目要求
给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
2.代码实现
public class MaxArry {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] array = {-2,11,-4,13,-5,-5,-2};
int result = maxSunArray(array);
System.out.println("连续子数组之最大和为:"+result);
}
public static int maxSunArray(int[] array) {
if (array.length==0 || array==null) {
return 0;
}
int Sum = 0;
int max = 0;
for (int i = 0; i < array.length; i++) {
if(Sum<=0){ //如果当前连续n项的和小于等于0,则没必要与后面的元素相加
Sum = array[i]; //Sum重新赋值
}else{
Sum += array[i]; //如果Sum的值大于0,则继续与后面的元素相加,
}
if(Sum>max){ //每次改变Sum的值都有与max进行比较
max = Sum; //如果Sum的值大于max,则将Sum的值赋值给max
}
}
return max;
}
}
代码中只用了一个for循环,所以其算法的时间复杂度为O(n)。
3.单元测试选择:条件组合覆盖
覆盖标准:
使得每个判定中条件的各种可能组合都至少出现一次。
其中条件选择的程序流程图如下
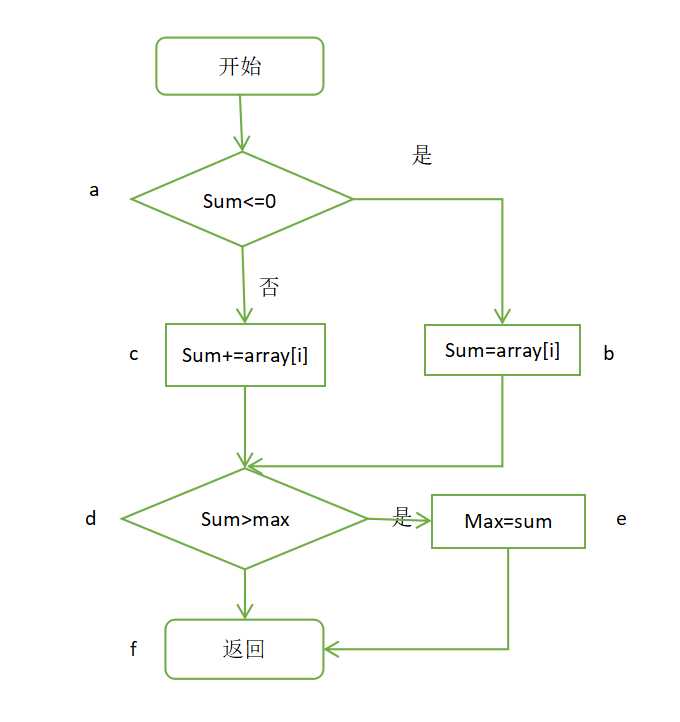
| sum<=0,sum>max |
abdef |
| sum>0,sum>max |
acdef |
| sum>0,sum>=max |
acdf |
| sum<=0,sum>=max |
abdf |
测试数据只需要一组[1,2,-3,2]即可实现上述四种执行路径
4.测试代码
import static org.junit.Assert.*;
import org.junit.Test;
public class ArrayMaxTest {
int[] array={1,2,-3,2};
@Test
public void MaxSunArrayTest() {
assertEquals(3,new ArrayMax().maxSunArray(array));
}
}
测试结果