??问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
??
- 算法分析:
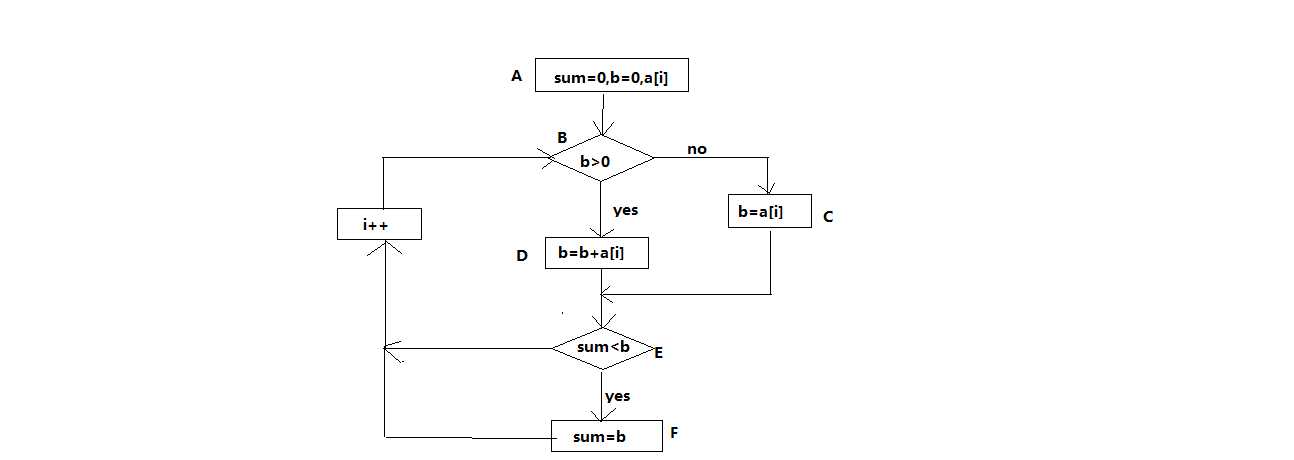
本题是为了求最大字段和,令b=sum=0。b用来存前i-1个数的和,sum用来存每一次i-1之前算出来的最大和。从数组第一个数开始,如果b小于0,b为当前的数,否则继续把当前数加上。如果新的和b大于原来的sum,就令sum=b;直到循环结束。程序流程图如下:
- 单元测试
程序的白盒测试有五种覆盖标准:语句覆盖,判定覆盖,条件覆盖,判定/条件覆盖 ,条件组合覆盖。
这次我采用条件判定覆盖。覆盖标准:使得判定中的每个条件获得各种可能的结果。
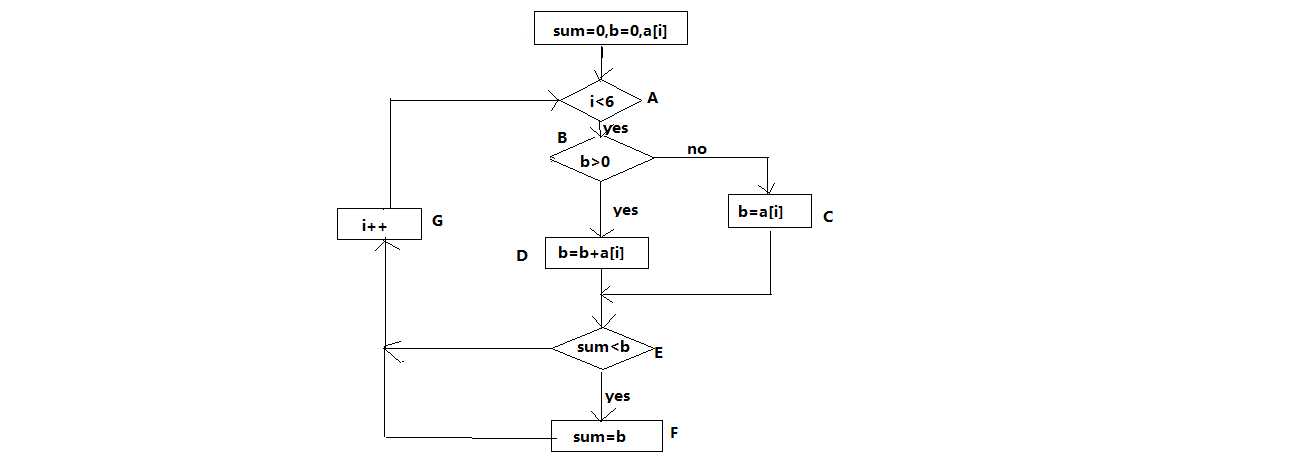
假设输入的数有6个,那么流程图如下:
即满足以下条件:1.b>0;
???? 2.sum<b;
???? 3.i<6;
满足以下覆盖情况:
判定一:i<6;i>=6
判定二:b>0;b<=0
判定三:sum
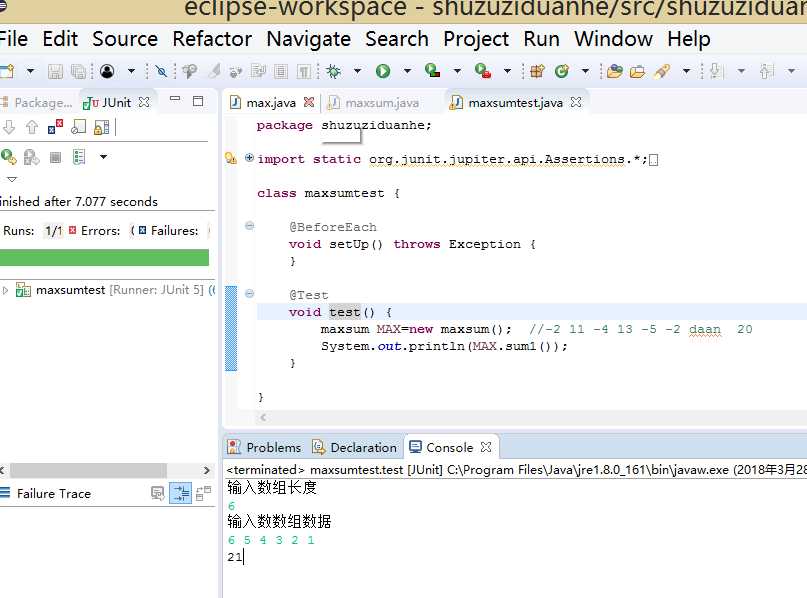
(1 2 3 4 5 6 7) (28) ABDEG (i>=6;b>0;sum<b) 结果出错。如图: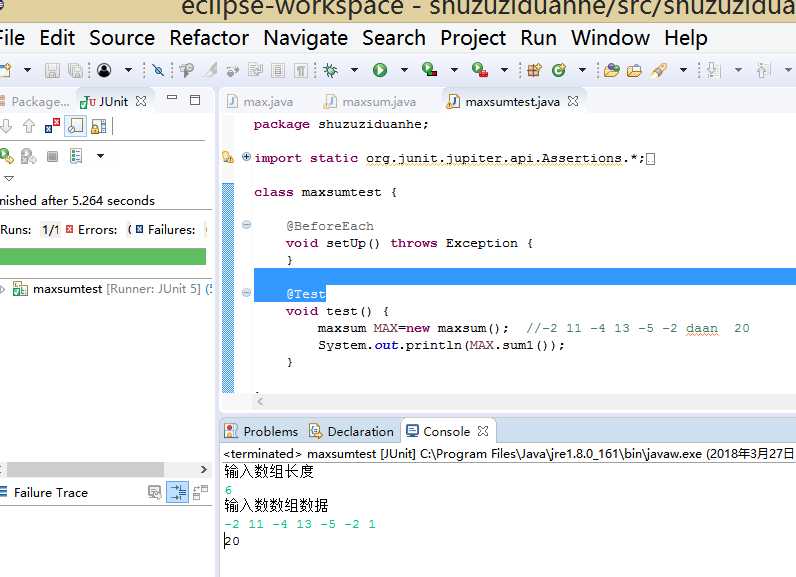
(-2 -5 -6 -7 -8 -9) (0) ABCEG (i<6;b<0;sum<b) 结果正确。如图: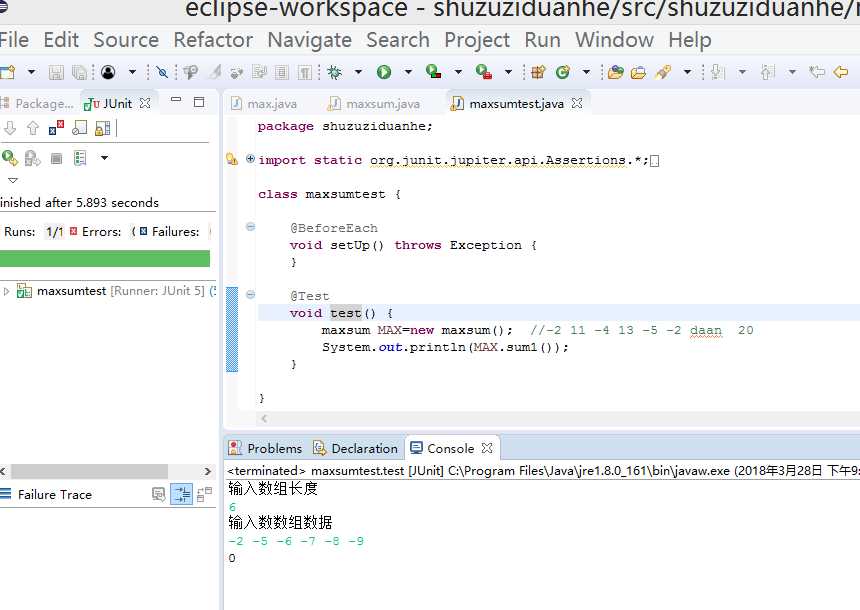
(6 5 4 3 2 1) (21) ABDEFG (I<6;b>0;sum>b) 结果正确。如图: