文中的一些图片以及思想很多都是参考https://www.cnblogs.com/My-code-z/p/5712524.html 大佬的思想 以及自己做一些个人理解的补充
细化算法原理理解起来并不难,借助矩阵九宫格来实现。将九宫格定义并且编号成如下格式。
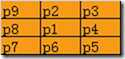
在讲解之前有必要先看看书中是怎么说的:


书中说的还是比较简洁的,毕竟是大牛写的,他们觉得很简单容易理解的东西,我们看起来就未必是这样了。好了闲话不多说 进入主题。
第一步:为了不影响原图像的一些其他操作,先将原图像拷贝一份用来细化处理,在将细化后图片返回出去。
第二步:就跟书里看的那样,需要满足四个条件来才能进行删除该点像素。这里进行的是沿着东南边界开始删除
1: a. 2<= p2+p3+p4+p5+p6+p7+p8+p9<=6
大于等于2会保证p1点不是端点或孤立点,因为删除端点和孤立点是不合理的,小于等于6保证p1点是一个边界点,而不是一个内部点。等于0时候,周围没有等于1的像素,所以p1为孤立点,等于1的时候,周围只 有1个灰度等于1的像素,所以是端点(注:端点是周围有且只能有1个值为1的像素)。

2:这里需要满足T(p1)=1 这里的T(p1)指的是以p2,p3...p8p9 就是p1邻居点进行轮转
这里的轮转就是从p2开始不断的与后面的点进行组成元组的格式 比如(p2,p3)(p3,p4) (p4,p5)。。。(p9,p2) 看看这样组成的所有元组为(0,1)格式的是否恰好为1个
假如为1个并且同时满足另外三个条件,那么他的样子大概会是这样的[[0,1,1] 这样轮转中就恰好有一个(0,1) 并且与1相邻的点必然还有像素值1 这样就是一个联通的区域 这时候p1就是边界点可以删除。
[0,1,0]
[0,0,0]]
大概的意思就是这样,我语文不好,不能说的很清楚,不过你们用本子画画就能理解我的意思了 见谅哈!!
3: P2*p4*p6 = 0
4: p4*p6*p8 = 0
这里 p4,p6出现了两次 在加上面的轮转判断 如果满足边界点条件 那么p4,p6中必然会有一个为0 至于为什么是p4,p6 就是因为这里是先沿着东南边界进行细化
将满足的点的索引值存入一个数组中,根据这个数组中点的索引值坐标 将图像中相应位置的点值置为0 完成一次边缘细化
第三步:这里是沿着西北方向进行细化
跟上面一步条件几乎一样,唯一改变就是第三和第四个条件,因为这里是为了沿着西北方向细化所以要调整为:p2*p4*p8 = 0 p2*p6*p8 = 0 这里的p2,p8出现两次的原因和 上面一步的p4,p6一样
将满足的点的索引值存入一个数组中,根据这个数组中点的索引值坐标 将图像中相应位置的点值置为0 完成一次边缘细化
最后:反复执行 第二步和第四步,不断的进行 左右的细化 直到没有点在可以细化 那么我们就得到了 细化后的骨架结构
现在原理已经解释完毕,那么就来看看python 是如何实现细化算法的
def neighbours(x,y,image): "Return 8-neighbours of image point P1(x,y) img = image x_1, y_1, x1, y1 = x-1, y-1, x+1, y+1 return [ img[x_1][y], img[x_1][y1], img[x][y1], img[x1][y1], # P2,P3,P4,P5 img[x1][y], img[x1][y_1], img[x][y_1], img[x_1][y_1] ] # P6,P7,P8,P9 def transitions(neighbours): n = neighbours + neighbours[0:1] # P2, P3, ... , P8, P9, P2 return sum( (n1, n2) == (0, 1) for n1, n2 in zip(n, n[1:]) ) # (P2,P3), (P3,P4), ... , (P8,P9), (P9,P2) #将白色静脉区域细化成骨架结构 def Refine(image): Image_Thinned = image.copy() # deepcopy to protect the original image changing1 = changing2 = 1 # the points to be removed (set as 0) while changing1 or changing2: # iterates until no further changes occur in the image # Step 1 changing1 = [] rows, columns = Image_Thinned.shape # x for rows, y for columns for x in range(1, rows - 1): # No. of rows for y in range(1, columns - 1): # No. of columns P2,P3,P4,P5,P6,P7,P8,P9 = n = neighbours(x, y, Image_Thinned) if (Image_Thinned[x][y] == 1 and # Condition 0: Point P1 in the object regions 2 <= sum(n) <= 6 and # Condition 1: 2<= N(P1) <= 6 The guarantee is not an isolated point and an endpoint or an internal point transitions(n) == 1 and # Condition 2: S(P1)=1 (0,1)The number of rotation of the structure is 1, and the boundary point can be determined by adding other conditions P2 * P4 * P6 == 0 and # Condition 3 Remove the southeast boundary point P4 * P6 * P8 == 0): # Condition 4 changing1.append((x,y)) for x, y in changing1: Image_Thinned[x][y] = 0 # Step 2 changing2 = [] for x in range(1, rows - 1): for y in range(1, columns - 1): P2,P3,P4,P5,P6,P7,P8,P9 = n = neighbours(x, y, Image_Thinned) if (Image_Thinned[x][y] == 1 and # Condition 0 2 <= sum(n) <= 6 and # Condition 1 transitions(n) == 1 and # Condition 2 P2 * P4 * P8 == 0 and # Condition 3 remove the northwest border point P2 * P6 * P8 == 0): # Condition 4 changing2.append((x,y)) for x, y in changing2: Image_Thinned[x][y] = 0 return Image_Thinned
虽然我英文很差,但是我有百度翻译啊 ,就将我所有的注释都翻译成了英文。
这里我指给出了算法的函数原型,至于怎么调用中间的代码我就不给了,反正如果你需要用到这个算法,只要将归一化到(0,1)二值的话图片传入进来调用就行了
在看看细化后的效果图
原图:
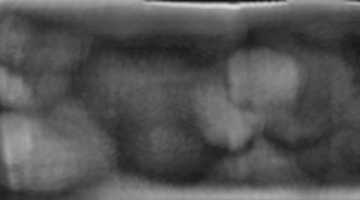
细化后的图片:
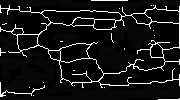
原图的静脉是黑色的 后面我在处理的时候 将黑白二值化翻转了 白色代表静脉区域
总结归纳:
1,看的出来这个细化算法还是有不足的,没有那么的美观,图像在分叉点处存在像素的冗余,即非单像素点,这会使得以后对特征点的提取相当的麻烦。
这就需要对细化算法进行改进了,这里可以采用一些模板算子对图像进行除去。
2,至于原手指静脉图像中的噪声和阴影等会在骨架图像中产生各种毛刺,这些毛刺也会影响后期的处理。除去毛刺可以通过从每个端点开始沿着费零点搜索,直到
交叉点时停止。在这个过程中,记录下每个端点上遍历的点数,然后取一个阈值,将小于阈值的那个端点搜索路径上的置为0。这样就完成了对图像的裁剪。
