一、哈夫曼树

1. 哈夫曼树也称最优二叉树。

　叶子节点的权值是对叶子节点赋予的一个有意义的数值量。

　设二叉树具有 n 个带权值的叶子结点，从根节点到各个叶子结点的路径长度与相应叶子结点权值的乘积之和叫做二叉树的带权路径长度。

　给定一组具有确定权值的叶子结点，可以构造处不同的二叉树，将其中带权路径长度最小的二叉树称为哈夫曼树。

2. 基本思想：

• 初始化：由给定的 n 个权值 $\left\{ \omega_{1},\omega_{2},\cdots ,\omega_{n}\right\}$构造 n 棵只有一个根节点的二叉树，从而得到一个二叉树集合$F=\left\{T_{1},T_{2},\cdots,T_{n}\right\}$。
• 选取与合并：在$F$中选取根节点的权值最小的两颗二叉树分别作为左右子树构造一棵新的二叉树（一般情况下将权值大的结点作为右子树。），这棵新二叉树的根节点的权值为其左、右子树根节点的权值之和。
• 删除与加入：在$F$中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到$F$中。
• 重复上述两个步骤，当集合$F$中只剩下一棵二叉树时，这棵二叉树便是哈夫曼树。

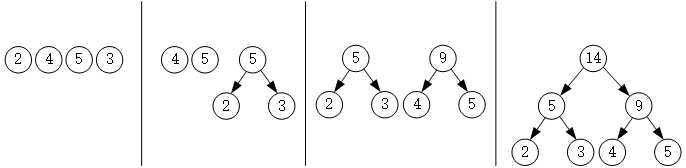
　　由哈夫曼算法构造的哈夫曼树中，非叶子节点的度均为2。具有 n 个叶子结点的哈夫曼树公有 2n-1个结点，其中有 n-1 个非叶子结点。它们是在 n-1 次的合并过程中生产的。

二、哈夫曼编码

1. 哈夫曼编码是一种可变字长编码

　如果一组编码中任一编码都不是其他任何一个编码的前缀，我们称这组编码为前缀编码。哈夫曼树可用于构造最短的不等长编码方案。

2. 算法流程

　　规定哈夫曼编码树的作分支代表 0，右分支代表 1，则从根结点到每个叶子结点所经过的路径组成的 0 和 1 的序列便成为该叶子结点对应字符的编码。

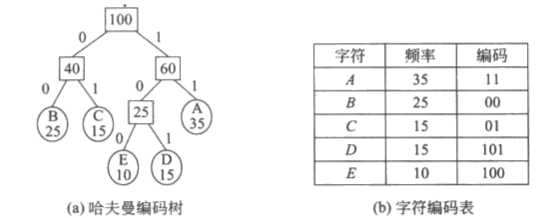
　　解码则是将编码串从左到右逐位判别，直到确定一个字符。

　　哈夫曼编码树中，树的带权路径长度的含义是各个字符的码长与其出现次数的乘积之和，所以采用哈夫曼树构造的编码是一种能使字符串的编码总长度最短的不等长编码。