一,无向图的割点与桥
对于G=(V,E)
1.割点:xξV若删除x以及与x所连边后,图被分裂成为多个联通图,则x为图的割点
2.桥(割边):eξE若删除e后图,图被分裂成为多个联通图,则e为图的割点
怎样求割点与割边
tarjan算法

就是他了。。。
首先我们引入时间戳的概念
设dfsn[x]表示从源节点Y开始访问到的第几个
也就是说我们假设dfsn[Y]=1,然后我们采用深度优先搜索树对图进行访问
依次对图的访问次序进行标记
如图:
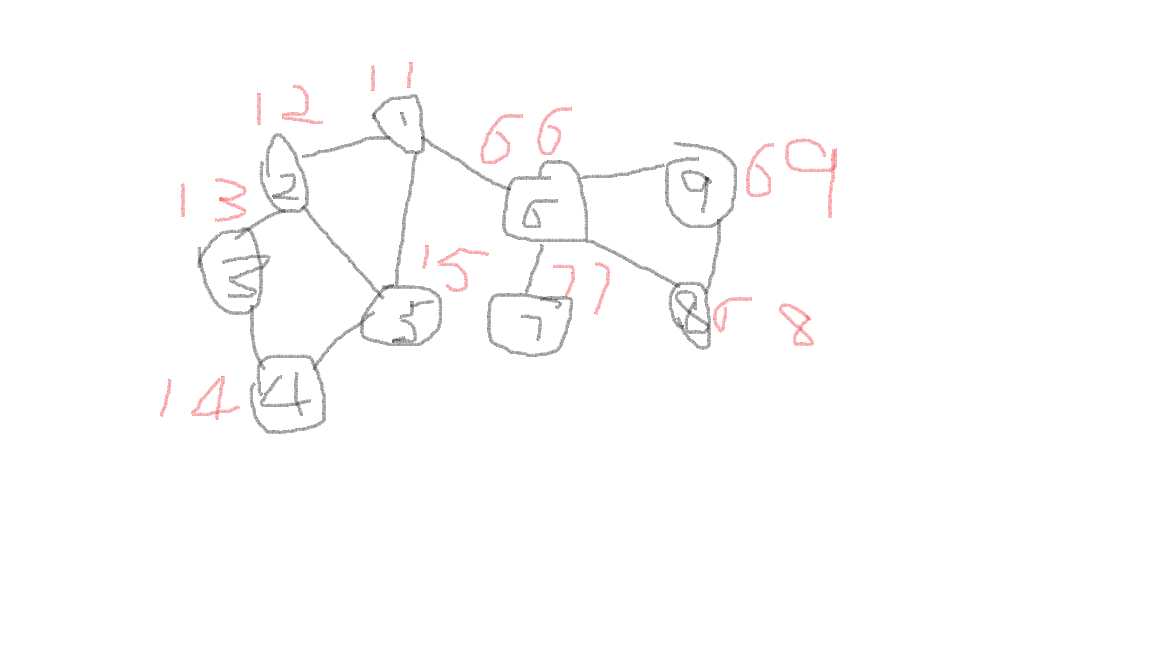
图中红色数字左表示low[x]值,右表示dfsn[x]值
什么是low[x],值呢?
我们定义low[x]表示x通过它的子树所能到达的最早编号的节点的编号
如何更新low[x]值?
我们在dfs过程中,先让low[x]=dfsn[x]
有定义可知,设y为x子节点,则low[x]=min(low[x],low[y]);
如图,我们会发现节点5可以不通过它的父节点而到达节点1
所以,同样low[x]=min(low[x],dfsn[y])
怎样判断点是否为割点?
dfsn[x]<=low[x]
怎样判断边是否为割边?
dfsn[x]<low[y]
(x,y)为割边
割点代码
