前一天,我们基于sklearn科学库实现了ID3的决策树程序,本文将基于python自带库实现ID3决策树算法。
一、代码涉及基本知识
1、 为了绘图方便,引入了一个第三方treePlotter模块进行图形绘制。该模块使用方法简单,调用模块createPlot接口,传入一个树型结构对象,即可绘制出相应图像。
2、 在python中,如何定义一个树型结构对象
可以使用了python自带的字典数据类型来定义一个树型对象。例如下面代码,我们定义一个根节点和两个左右子节点:
rootNode = {‘rootNode‘: {}}
leftNode = {‘leftNode‘: {‘yes‘:‘yes‘}}
rightNode = {‘rightNode‘: {‘no‘:‘no‘}}
rootNode[‘rootNode‘][‘left‘] = leftNode
rootNode[‘rootNode‘][‘right‘] = rightNode
treePlotter.createPlot(rootNode)
通过调用treePlotter模块,绘制出如下树的图像
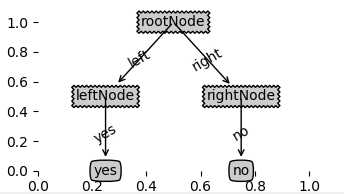
2、 递归调用
为了求每个节点的各个子节点,要用到递归的方法来实现,基本思想和二叉树的遍历方法一致,后面我们还会用Python实现一个二叉树源码,此处不再进行介绍。
3、 此外,还需要对python常用的数据类型及其操作比较了解,例如字典、列表、集合等
二、程序主要流程
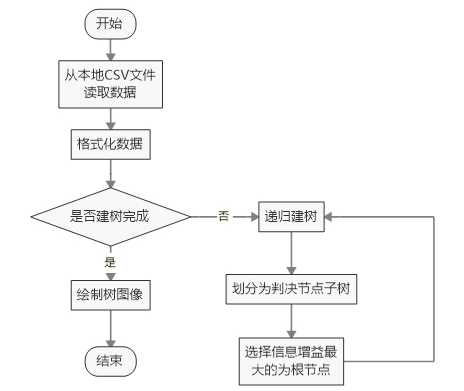
三、测试数据集
|
age |
income |
student |
credit_rating |
class_buys_computer |
|
youth |
high |
no |
fair |
no |
|
youth |
high |
no |
excellent |
no |
|
middle_aged |
high |
no |
fair |
yes |
|
senior |
medium |
no |
fair |
yes |
|
senior |
low |
yes |
fair |
yes |
|
senior |
low |
yes |
excellent |
no |
|
middle_aged |
low |
yes |
excellent |
yes |
|
youth |
medium |
no |
fair |
no |
|
youth |
low |
yes |
fair |
yes |
|
senior |
medium |
yes |
fair |
yes |
|
youth |
medium |
yes |
excellent |
yes |
|
middle_aged |
medium |
no |
excellent |
yes |
|
middle_aged |
high |
yes |
fair |
yes |
|
senior |
medium |
no |
excellent |
no |
四、程序代码
1、计算测试集熵及信息增益
# 求最优的根节点 def chooseBestFeatureToSplit(dataset,headerList): # 定义一个初始值 bestInfoGainRate = 0.0 bestFeature = 0 # 求特征列项的数量 numFeatures = len(dataset[0]) -1 # 获取整个测试数据集的熵 baseShnnonEnt = calcShannonEnt(dataset) print("total‘s shannonEnt = %f" % (baseShnnonEnt)) # 遍历每一个特征列,求取信息增益 for i in range(numFeatures): # 获取某一列所有特征值 featureList = [example[i] for example in dataset] uniqueVals = set(featureList) newEntropy = 0.0 # 求得某一列某一个特征值的概率和熵 newShannonEnt = 0.0 for value in uniqueVals: # 计算熵 subDataset = splitDataSet(dataset,i,value) newEntropy = calcShannonEnt(subDataset) # 计算某一列某一个特征值的概率 newProbability = len(subDataset) / float(len(dataset)) newShannonEnt += newProbability*calcShannonEnt(subDataset) infoGainRate = baseShnnonEnt - newShannonEnt print("%s‘s infoGainRate = %f - %f = %f"%(headerList[i],baseShnnonEnt,newShannonEnt,infoGainRate)) if infoGainRate > bestInfoGainRate: bestInfoGainRate = infoGainRate bestFeature = i return bestFeature
该结果和前一天计算结果一致,age特征对应信息增益最大,因此设为根节点:

2、程序源码
treePlotter.py
import matplotlib.pyplot as plt # 定义决策树决策结果属性 descisionNode = dict(boxstyle=‘sawtooth‘, fc=‘0.8‘) leafNode = dict(boxstyle=‘round4‘, fc=‘0.8‘) arrow_args = dict(arrowstyle=‘<-‘) def plotNode(nodeTxt, centerPt, parentPt, nodeType): # nodeTxt为要显示的文本,centerNode为文本中心点, nodeType为箭头所在的点, parentPt为指向文本的点 createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords=‘axes fraction‘, xytext=centerPt, textcoords=‘axes fraction‘, va=‘center‘, ha=‘center‘, bbox=nodeType, arrowprops=arrow_args) def getNumLeafs(myTree): numLeafs = 0 firstStr = list(myTree.keys())[0] secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__ == ‘dict‘: numLeafs += getNumLeafs(secondDict[key]) else: numLeafs += 1 return numLeafs def getTreeDepth(myTree): maxDepth = 0 firstStr = list(myTree.keys())[0] # 这个是改的地方,原来myTree.keys()返回的是dict_keys类,不是列表,运行会报错。有好几个地方这样 secondDict = myTree[firstStr] for key in secondDict.keys(): if type(secondDict[key]).__name__ == ‘dict‘: thisDepth = 1 + getTreeDepth(secondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth def createPlot(inTree): fig = plt.figure(1, facecolor=‘white‘) fig.clf() axprops = {‘xticks‘: None, ‘yticks‘: None} createPlot.ax1 = plt.subplot(111, frameon=False) plotTree.totalW = float(getNumLeafs(inTree)) # 全局变量宽度 = 叶子数目 plotTree.totalD = float(getTreeDepth(inTree)) # 全局变量高度 = 深度 plotTree.xOff = -0.5/plotTree.totalW plotTree.yOff = 1.0 plotTree(inTree, (0.5, 1.0), ‘‘) plt.show() def plotTree(myTree, parentPt, nodeTxt): numLeafs = getNumLeafs(myTree) depth = getTreeDepth(myTree) firstStr = list(myTree.keys())[0] # cntrPt文本中心点, parentPt指向文本中心的点 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) plotMidText(cntrPt, parentPt, nodeTxt) plotNode(firstStr, cntrPt, parentPt, descisionNode) seconDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD for key in seconDict.keys(): if type(seconDict[key]).__name__ == ‘dict‘: plotTree(seconDict[key], cntrPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW plotNode(seconDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD def plotMidText(cntrPt, parentPt, txtString): xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0] yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1] createPlot.ax1.text(xMid, yMid, txtString, va=‘center‘, ha=‘center‘, rotation=30)
decision_tree_ID3.py
# 导入库 import csv import math import operator import treePlotter # 导入数据集 def readDataset(file_path,file_mode): allElectronicsData = open(file_path, file_mode) reader = csv.reader(allElectronicsData) # 读取特征名称 headers = next(reader) # 读取测试数据集 dataset = [] for row in reader: dataset.append(row) return headers,dataset # 求某个数据集的熵 def calcShannonEnt(dataset): shannonEnt = 0.0 labelList = {} for vec_now in dataset: labelValue = vec_now[-1] if vec_now[-1] not in labelList.keys(): labelList[labelValue] = 0 labelList[labelValue] += 1 for labelKey in labelList: probability = float(labelList[labelKey] / len(dataset)) shannonEnt -= probability*math.log(probability,2) return shannonEnt # 根据给定的列特征值,分理出给定的特征量 def splitDataSet(dataset,feature_seq,value): new_dataset = [] for vec_row in dataset: feature_Value = vec_row[feature_seq] if feature_Value == value: temp_vec = [] temp_vec = vec_row[:feature_seq] temp_vec.extend(vec_row[feature_seq+1:]) new_dataset.append(temp_vec) return new_dataset # 求最优的根节点 def chooseBestFeatureToSplit(dataset,headerList): # 定义一个初始值 bestInfoGainRate = 0.0 bestFeature = 0 # 求特征列项的数量 numFeatures = len(dataset[0]) -1 # 获取整个测试数据集的熵 baseShnnonEnt = calcShannonEnt(dataset) #print("total‘s shannonEnt = %f" % (baseShnnonEnt)) # 遍历每一个特征列,求取信息增益 for i in range(numFeatures): # 获取某一列所有特征值 featureList = [example[i] for example in dataset] uniqueVals = set(featureList) newEntropy = 0.0 # 求得某一列某一个特征值的概率和熵 newShannonEnt = 0.0 for value in uniqueVals: # 计算熵 subDataset = splitDataSet(dataset,i,value) newEntropy = calcShannonEnt(subDataset) # 计算某一列某一个特征值的概率 newProbability = len(subDataset) / float(len(dataset)) newShannonEnt += newProbability*calcShannonEnt(subDataset) infoGainRate = baseShnnonEnt - newShannonEnt #print("%s‘s infoGainRate = %f - %f = %f"%(headerList[i],baseShnnonEnt,newShannonEnt,infoGainRate)) if infoGainRate > bestInfoGainRate: bestInfoGainRate = infoGainRate bestFeature = i return bestFeature # 标签判定,通过少数服从多数原则 def majorityCnt(classList): classcount = {} for cl in classList: if cl not in classcount.keys(): classcount[cl] = 0 classcount[cl] += 1 sortedClassCount = sorted(classcount.items(),key = operator.itemgetter(1),reverse= True) return sortedClassCount[0][0] # 创建一个决策树 def createTree(dataSet, labels): classList = [example[-1] for example in dataSet] # 1 所有特征值都是相同的时候直接返回 if classList.count(classList[0]) == len(classList): return classList[0] # 2 遍历完所有特征值,投票原则,返回出现次数最多的标签 if len(dataSet[0]) == 1: return majorityCnt(classList) # 3 如果不满足上面两者,求最优特征 bestFeature = chooseBestFeatureToSplit(dataSet,labels) bestFeatureLabel = labels[bestFeature] myTree = {bestFeatureLabel: {}} del (labels[bestFeature]) featurValues = [example[bestFeature] for example in dataSet] uniqueVals = set(featurValues) # 使用递归的方法,获得整个树 for value in uniqueVals: subLabels = labels[:] myTree[bestFeatureLabel][value] = createTree(splitDataSet(dataSet, bestFeature, value), subLabels) return myTree def classify(inputTree, featLabels, testVec): firstStr = list(inputTree.keys())[0] secondDict = inputTree[firstStr] featIndex = featLabels.index(firstStr) for key in secondDict.keys(): if testVec[featIndex] == key: if type(secondDict[key]).__name__ == ‘dict‘: classLabel = classify(secondDict[key], featLabels, testVec) else: classLabel = secondDict[key] return classLabel def classifyAll(inputTree, featLabels, testDataSet): classLabelAll = [] for testVec in testDataSet: classLabelAll.append(classify(inputTree, featLabels, testVec)) return classLabelAll def storeTree(inputTree, filename): import pickle fw = open(filename, ‘wb‘) pickle.dump(inputTree, fw) fw.close() def grabTree(filename): import pickle fr = open(filename, ‘rb‘) return pickle.load(fr) def main(): # 读取数据集 labels, dataSet = readDataset(file_path=r‘D:\test.csv‘, file_mode=‘r‘) labels_tmp = labels[:] # 拷贝,createTree会改变labels desicionTree = createTree(dataSet, labels_tmp) storeTree(desicionTree, ‘classifierStorage.txt‘) desicionTree = grabTree(‘classifierStorage.txt‘) treePlotter.createPlot(desicionTree) testSet = [[‘youth‘, ‘high‘, ‘no‘, ‘fair‘, ‘no‘]] print(‘classifyResult:\n‘, classifyAll(desicionTree, labels, testSet)) if __name__ == ‘__main__‘: main()
五、测试结果及结论
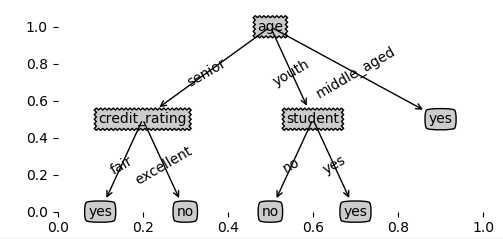
我们从上面求解信息增益的公式中,其实可以看出,信息增益准则其实是对可取值数目较多的属性有所偏好!
现在假如我们把数据集中的“编号”也作为一个候选划分属性。我们可以算出“编号”的信息增益是0.998
因为每一个样本的编号都是不同的(由于编号独特唯一,条件熵为0了,每一个结点中只有一类,纯度非常高啊),也就是说,来了一个预测样本,你只要告诉我编号,其它特征就没有用了,这样生成的决策树显然不具有泛化能力。
参考链接:
http://www.cnblogs.com/wsine/p/5180310.html
https://zhuanlan.zhihu.com/p/26760551
