2018-04-0517:12:14
第一次复现论文,打个卡
结果:
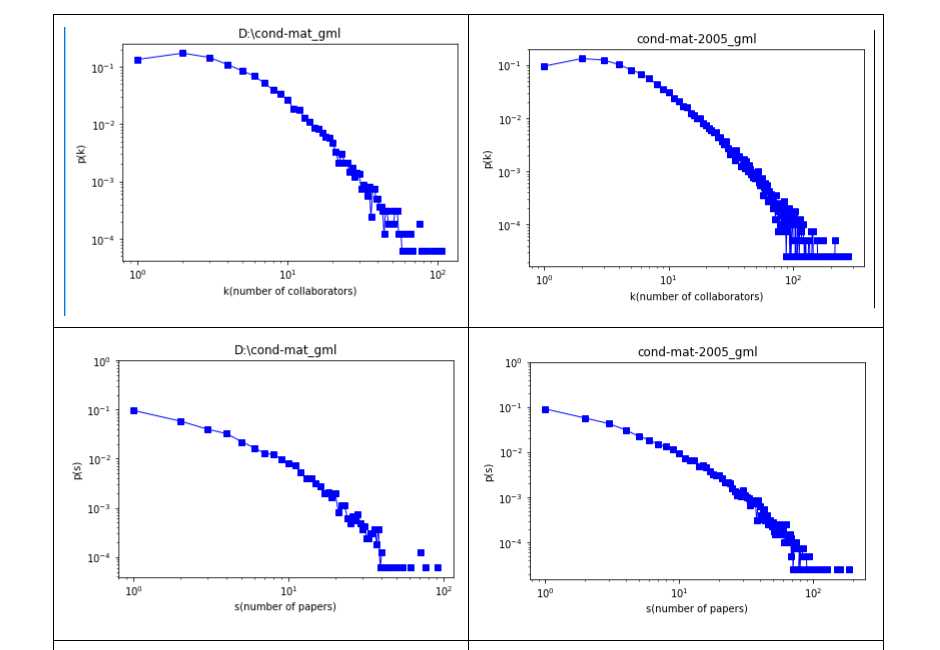
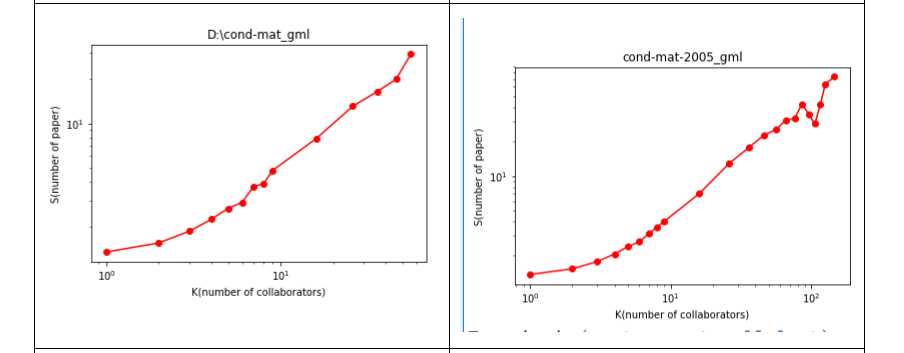
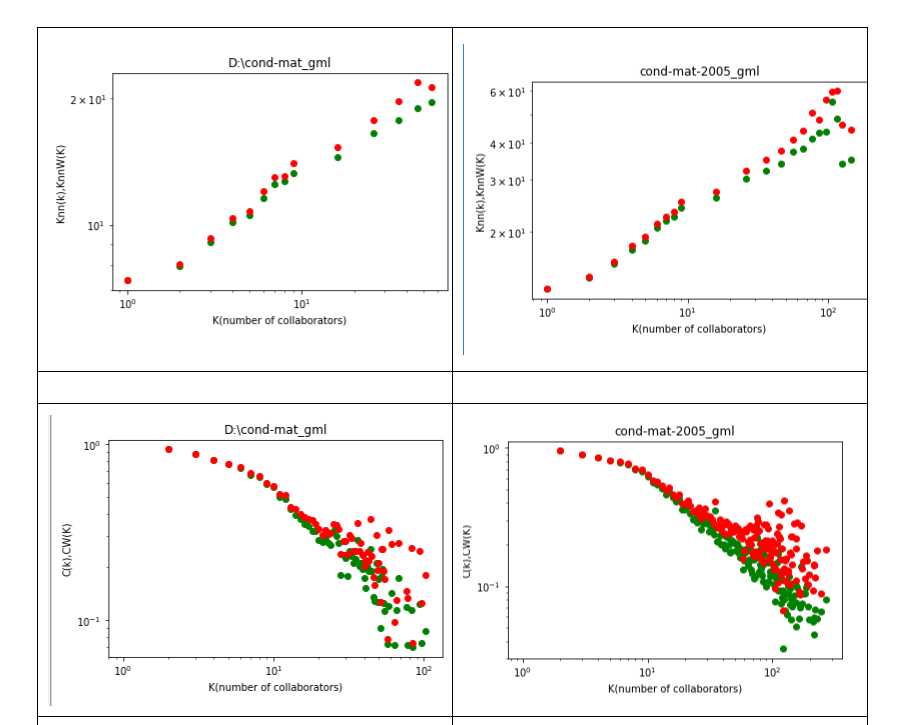
数据:
https://pan.baidu.com/s/1_rMS-_VGrJPLtHz_ssfL9Q
代码1:
import networkx as nx import matplotlib.pyplot as plt #import pandas as pd #from networkx.algorithms import approximation as approx #复现论文Alain Barrat.Modeling the evolutio of Weighted networks #yyh #2018/3/24 pathOfFile1 = "D:\soft\cond-mat_gml.adj"; pathOfFile2 = "D:\soft\cond-mat-2005_gml.adj"; title1 = "D:\cond-mat_gml"; title2 = "cond-mat-2005_gml"; #读入数据,返回无向加权graph def createGraph(filename) : G = nx.Graph() for line in open(filename) : strlist = line.split() n1 = int(strlist[0]) n2 = int(strlist[1]) weight = float(strlist[2]) G.add_weighted_edges_from([(n1, n2, weight)]) return G #test GG = createGraph(pathOfFile1); #得到每一个顶点的strength def getStrengthList(G): nodelist = G.nodes(); strengthlist =[]; for i in nodelist: strengthlist.append(G.degree(i,weight=‘weight‘)); return strengthlist #得到强度的字典 #返回字典 def getStrengthDic(G): strengthDic = {}; strengthlist = getStrengthList(G); nodelist = G.nodes(); count = 0; for i in nodelist: strengthDic[i] = strengthlist[count]; count = count+1; return strengthDic; # strengthDic = getStrengthDic(G); #得到每一个顶点的degree #返回字典 def getDegreeDic(G): return G.degree(); #返回每一个顶点的度 #返回列表 def getDegreeList(G): nodelist = G.nodes(); degreelist = []; degreeDic = getDegreeDic(G); for i in nodelist: degreelist.append(degreeDic[i]); return degreelist; #得到度的最大值和最小值,并且返回其值 def getMaxMinDegree(degreeDic): maxDegree=0; minDegree = 0; for k,v in degreeDic: if v>maxDegree: maxDegree = v; if v<minDegree : minDegree = v; return (maxDegree,minDegree); #得到每个顶点的聚集系数 #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #介绍的公式与networkx中API 数学公式一致 #返回字典 def getCiDic(G): clusteringdic = nx.clustering(G,nodes=None,weight=None); return clusteringdic; #得到每个顶点的加权聚集系数 #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #介绍的公式CiW = 1/si/(ki-1)*sum((wij+wih)/2|i,j,h,互连) #返回字典 def getCiWDic(G): strengthlist = getStrengthList(G); degreedic = G.degree(); nodelist = G.nodes(); cw = {}; sum = 0; count = 0; for i in nodelist: si = strengthlist[count]; count = count+1; neibors= G.neighbors(i); ki = degreedic[i]; if ki>1: #最起码构成三角形,若不能则默认为0 sum = 0; for j in neibors: for h in G.neighbors(j): if G.get_edge_data(i,h)!=None: wij = G.get_edge_data(i,j)[‘weight‘]; wih = G.get_edge_data(i,h)[‘weight‘]; sum +=(wij+wih)/2;# 注意在这个地方要除以4 因为多计算了一遍 ciw = 1/(si*(ki-1))*sum; cw[i] = ciw; else: cw[i]=0; return cw ; #test cw = getCWDic(G); #得到每个顶点的近邻度 #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #介绍的公式Knni = 1/Ki*sum(kj|j,i相连) #返回字典 def getKnnDic(G): degreeDic = getDegreeDic(G); knnDic = {}; nodes = G.nodes(); for i in nodes: ki = degreeDic[i]; if ki>0: #当该顶点没有近邻点是默认为0 neighborOfi = G.neighbors(i); sum = 0; for j in neighborOfi: kj = degreeDic[j]; sum += kj; knni = 1/ki*sum; else: knni = 0; knnDic[i] = knni; return knnDic; #knnDic = getKnnDic(G) #得到每个顶点的加权近邻度 #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #介绍的公式knnwi = 1/si*sum(wij*kj) def getKnnWDic(G): strengthDic = getStrengthDic(G); degreeDic = getDegreeDic(G); nodes = G.nodes(); knnw = {}; for i in nodes: sum = 0; si = strengthDic[i]; if si>0: #若是孤立的顶点则为0 for j in G.neighbors(i): wij = G.get_edge_data(i,j)[‘weight‘]; #得到ji 之间的权值 kj = degreeDic[j]; sum += wij*kj; knnwi = 1/si*sum; else: knnwi = 0; knnw[i] = knnwi; return knnw; #返回一个节点的所有信息 #包括节点编号,顶点的度,顶点的强度,顶点的聚集系数, #顶点的加权聚集系数,顶点的近邻度 #顶点的加权近邻度 def getMessaures(G): return 0; #全概率公式 #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #介绍的公式C(k) = sum(Ki*p(ki/k)) #每一个度对应的KNNWOFK #返回字典 def getKnnOfKDic(G): knnDic = getKnnDic(G); degreeDic = getDegreeDic(G); return getAvarageOfKDic(knnDic,degreeDic); #每一个度的对应的KNNW #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #返回字典 def getKnnWOfKDic(G): knnWDic = getKnnWDic(G); degreeDic = getDegreeDic(G); return getAvarageOfKDic(knnWDic,degreeDic); #全概率公式 #根据论文 Alain Barrat.Modeling the evolutio of Weighted networks中 #介绍的公式C(K) = 1/NP(K)*sum(Ci|i/ki=k) #每一个度对应的CiK #返回字典 def getCiOfkDic(G): ciDic = getCiDic(G); degreeDic = getDegreeDic(G); return getAvarageOfKDic(ciDic,degreeDic); #利用概率公式 #每个度对应的CIW #返回字典 def getCiWOfKDic(G): ciWDic = getCiWDic(G); degreeDic = getDegreeDic(G); return getAvarageOfKDic(ciWDic,degreeDic); #利用概率公式 #每个度对应的平均strength #返回字典 def getStrengthOfKDic(G): strengthDic = getStrengthDic(G); degreeDic= getDegreeDic(G); return getAvarageOfKDic(strengthDic,degreeDic); #统计strength 频数 按照区间来进行统计 #strength可能是一个浮点数 #按照 def getStrengthcountList(G): strengthlist =getStrengthList(G); #频度统计,统计max-min,将其化成整数值,依照区间来进行频数统计 strengthlist.sort(reverse = False) maxstrength = max(strengthlist); minstrength = min(strengthlist); splitnum = int(maxstrength- minstrength);#区间数目 strengthcount = [0 for i in range(splitnum)]; spli = float(maxstrength-minstrength)/(splitnum-1); #注意此处splitnum-1 for i in strengthlist: index = (int((i-minstrength)/spli)); #print(index) strengthcount[index] = strengthcount[index]+1 ; return strengthcount; #绘制双对数分布图形 def ploDistrbution(countList,xlabel,ylabel,title): #plt.figure(figsize=(500, 500)); x = range(len(countList)) y = [z / float(sum(countList)) for z in countList] plt.xlabel(xlabel); plt.ylabel(ylabel); plt.title(title); plt.loglog(x,y,color="blue",linewidth=1,marker = ‘s‘); plt.show()#显示图表 return ‘ok‘ #根据字典关键字来升序排序,采用选择排序法 #返回字典 def sortDic(dic): return sorted(dic.iteritems(),key=lambda abs:abs[0],reverse=False) #合并两个列表,返回字典 def mergeList(list1,list2): dic = {}; return dic; #合并两个字典,返回字典,对应合并 def mergeDic(dic1,dic2): dic = {}; for key,value in dic1: dic[value] = dic2[value]; return dic; #得到字典的keys列表 #得到字典的values列表 #返回其列表元组 def getKeysValuesListOfDic(dic): keys = dic.keys(); values = dic.values(); return (keys,values); #得到度量在K条件下的平均值 #返回字典(关于K条件下的平均值序列) def getAvarageOfKDic(metricDic,degreeDic): #得到度的范围 (maxDegree,minDegree) = getMaxMinDegree(degreeDic); avarageMetricsOfKDic = {}; #初始化 value = 0; #求和值 count=0; #计数度的个数 for k in range(maxDegree): value = 0; count = 0; for nodes,degree in degreeDic: if degree==k: count += 1; value +=metricDic[nodes]; if count>=1: value =float(value/count); else : value = 0; avarageMetricsOfKDic[k] = value; return avarageMetricsOfKDic; #绘制S与K的关系图 def plotStrengthAndDegree(G,kdic,xlabel,ylabel,title): strengthOfKDic = getStrengthOfKDic(G); strengthOfKDic = dataBanning( strengthOfKDic ,kdic); (x,y) = getKeysValuesListOfDic( strengthOfKDic); plt.xlabel(xlabel); plt.ylabel(ylabel); plt.title(title); plt.loglog(x,y,color="red",marker = ‘o‘); plt.show(); return ‘ok‘ #data Banning #输入列表或者是字典 #返回字典 def dataBanning(dicOfK,degreeDic): sum =0.0; count = 0; dic = {}; (maxDegree,minDDegree) = getMaxMinDegree(degreeDic); #print(maxDegree/10); for i in range(1,10): dic[i] = dicOfK[i]; for i in range(1,int(maxDegree/10)): sum=0; count =0; for j in range(0,9): if (i*10+j)<= maxDegree and dicOfK[i*10+j]!=0: sum += dicOfK[i*10+j]; count += 1; else: break; if count!=0: sum = sum/count; else: continue; dic[10*i+6] = sum; return dic; #绘制Ck,CWk #绘制KNNK,KNNWK def plotCompare(mic1,mic2,kdic,xlabel,ylabel,title): mic1Dic = dataBanning(mic1,kdic); (x,y1) = getKeysValuesListOfDic(mic1Dic); micW2Dic = dataBanning( mic2 ,kdic); (x,y2) = getKeysValuesListOfDic(micW2Dic) plt.xlabel(xlabel); plt.ylabel(ylabel); plt.title(title); plt.loglog(x, y1, ‘go‘, x, y2, ‘ro‘); plt.show(); return ‘OK‘; def test(G,title): #strengthcount = getStrengthcountList(G); #ploDistrbution(strengthcount,"s(number of papers)","p(s)",title) #plt.savefig("p(s).jpg") ; #degreecount = nx.degree_histogram(G) #ploDistrbution(degreecount,"k(number of collaborators)","p(k)",title) #plt.savefig(("p(k)"+title).jpg) ; degreeDic = getDegreeDic(G); #strengthlist = getStrengthDic(G); xlabel = ‘K(number of collaborators)‘; ylabel = ‘S(number of paper)‘; plotStrengthAndDegree(G,degreeDic,xlabel,ylabel,title) #绘制Ck,CWk ciOfKDic = getCiOfkDic(G); ciWOfKDic = getCiWOfKDic(G); plotCompare(ciOfKDic,ciWOfKDic, degreeDic,"K(number of collaborators)","C(K),CW(K)",title); #绘制Knnk,Knnwk knnOfKDic = getKnnOfKDic(G); knnWOfKDic = getKnnWOfKDic(G); plotCompare(knnOfKDic,knnWOfKDic, degreeDic,"K(number of collaborators)","Knn(k),KnnW(K)",title); return ‘ok‘; #test1 #G1 = createGraph(pathOfFile1); #test(G1,title1); #test2 G2 = createGraph(pathOfFile2); test(G2,title2) #绘制图形 #clusteringL = nx.clustering(G,nodes=None,weight=None) #clusteringDic = nx.clustering(G,nodes=None,weight=None); #G.get_edge_data(1,190)#查看固定的边 #n= len(G) #查看节点数 #聚集系数 #Clustering = nx.clustering(G) #网络度分布 #Degree_distribution = nx.degree_histogram(G) #网络度的中心性 #Degree_Centrality = nx.degree_centrality(G) #各个节点Closeness #Closeness_Centrality = nx.closeness_centrality(G) # #各个节点Betweenness # #Betweenness_Centrality = nx.betweenness_centrality(G) #nx.betweenness_centrality(G)????
