原创文章,转载请注明出处!
# 预备知识
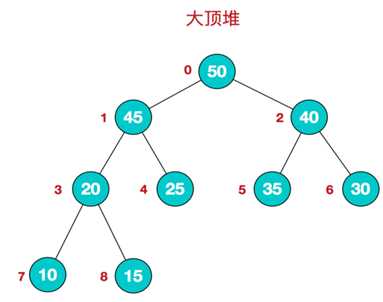
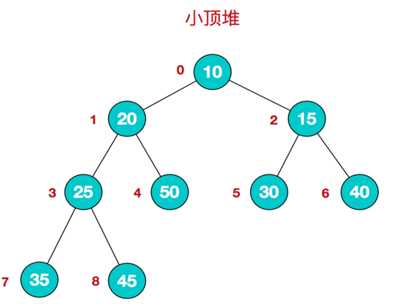
堆是一种特殊的树形数据结构,即完全二叉树。堆分为大根堆和小根堆,大根堆为根节点的值大于两个子节点的值;小根堆为根节点的值小于两个子节点的值,同时根节点的两个子树也分别是一个堆。
# 基本思路
- 步骤一:建立大根堆--将n个元素组成的无序序列构建一个大根堆,
- 步骤二:交换堆元素--交换堆尾元素和堆首元素,使堆尾元素为最大元素;
- 步骤三:重建大根堆--将前n-1个元素组成的无序序列调整为大根堆
重复执行步骤二和步骤三,直到整个序列有序。
# 图示说明
- 步骤一:建立大根堆
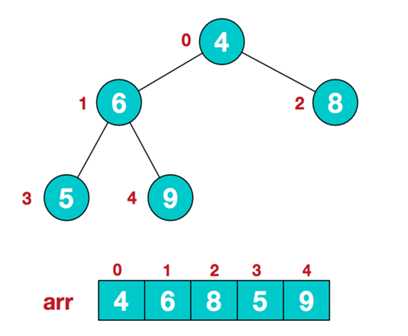
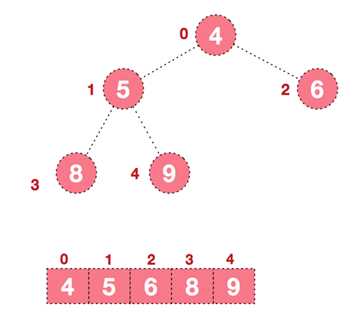
① 无序序列建立完全二叉树
② 从最后一个叶子节点开始,从左到右,从下到上调整,将完全二叉树调整为大根堆
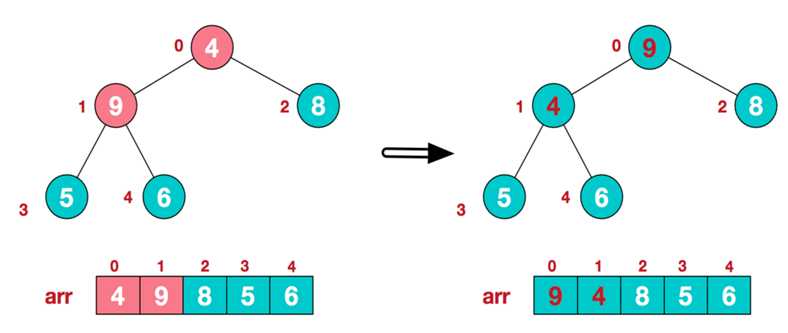
a.找到第一个非叶子结点8,由于8没有左右节点,所有不用调整
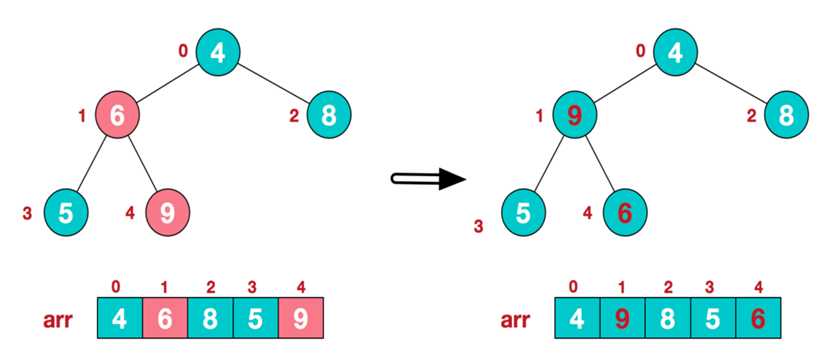
b.找到第二个非叶子节点6,由于6的右子节点9比6大,所以交换6和9。交换后,符合大根堆的结构。
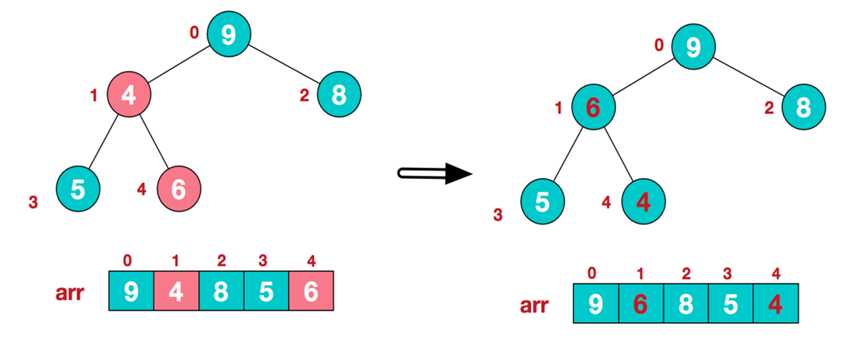
c.找到第三个非叶子节点4,由于的4左子节点9比4大,所以交换4和9。交换后不符合大根堆的结构,继续从右到左,从下到上调整。
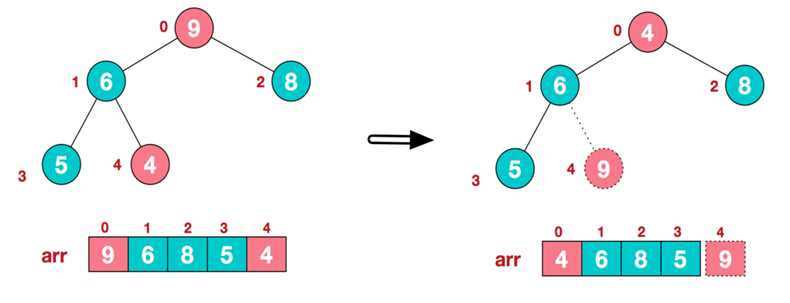
- 步骤二:交换堆元素(交换堆首和堆尾元素--获得最大元素)
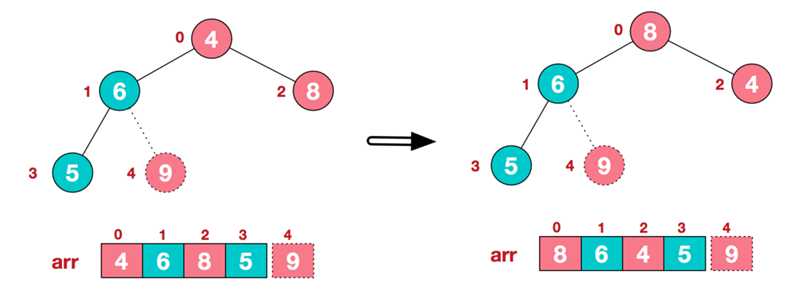
- 步骤三:重建大根堆(前n-1个元素)
- 重复执行步骤二和步骤三,直到整个序列有序
# C++代码
1 #include <iostream> 2 using namespace std; 3 int n; 4 int a[105]; 5 6 // 构建大根堆,其中a是第一个非叶子节点,z是节点个数 7 void HeapAdjust(int A[], int a, int z) 8 { 9 // 重建最大堆,i是父节点,j是左子节点 10 for(int i = a, j = 2 * i; j <= z; i = j, j = 2 * i) 11 { 12 // 取i的左右子节点中较大的子节点 13 if(j < z && A[j + 1] > A[j]) 14 j++; 15 16 if(A[i] < A[j]) 17 swap(A[i], A[j]); 18 else 19 break; 20 } 21 } 22 23 // 从右到做,从下到上 24 void HeapSort(int A[], int n) 25 { 26 // 第一步:建立大根堆(i是第一个非叶子节点,n是节点个数) 27 for(int i = n / 2; i >= 1; i--) 28 { 29 HeapAdjust(A, i, n); 30 } 31 32 for(int i = n; i >= 1; i--) 33 { 34 // 第二步:交换堆元素(堆首和堆尾) 35 swap(A[1], A[i]); 36 37 // 第三步:重建大根堆 38 HeapAdjust(A, 1, i - 1); 39 } 40 } 41 int main() 42 { 43 cin >> n; 44 for(int i = 1; i <= n; i++) 45 cin >> a[i]; 46 HeapSort(a, n); 47 for(int i = 1; i <= n; i++) cout << a[i] << " "; 48 cout << endl; 49 cout<<a[0]<<endl; 50 return 0; 51 }
文中配图参考地址