案例:通过分析上海的二手房的数据,分析出性价比(地段,价格,未来的升值空间)来判断哪个区位的二手房性价比最高
1.载入包
library(ggplot2)
library(Hmisc)
library(car)
library(caret)
2.加载数据集
houses <- read.csv(‘E:\\Udacity\\Data Analysis High\\R\\R_Study\\二手房分析案例\\链家二手房.csv‘,sep=‘,‘,header=T)
3.查看数据集
describe(houses)
数据集有以下几个字段构成
## 小区名称 ## 户型 ## 面积 ## 区域 ## 楼层 ## 朝向 ## 价格.W. ## 单价.平方米. ## 建筑时间
探究影响房价的主要因素是什么
4.查看户型的分布
type_freq <- data.frame(table(houses$户型)) type_p <- ggplot(data=type_freq,aes(x=reorder(Var1,-Freq),y=Freq))+ geom_bar(stat=‘identity‘,fill=‘steelblue‘)+ theme(axis.text.x = element_text(angle = 30,vjust = 0.5))+ xlab(‘户型‘)+ ylab(‘套数‘) type_p
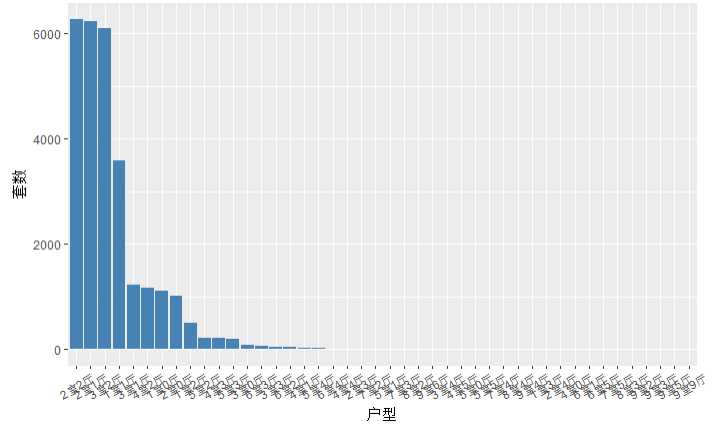
结论:户型的分布不符合正态分布
需要对户型的数据进行清洗,找出主要的户型
5.对户型数据进行清洗
# 把低于一千套的房型设置为其他 type <- c(‘2室2厅‘,‘2室1厅‘,‘3室2厅‘,‘1室1厅‘,‘3室1厅‘,‘4室2厅‘,‘1室0厅‘,‘2室0厅‘,‘4室1厅‘) houses$type.new <- ifelse(houses$户型 %in% type,as.character(houses$户型),‘其他‘) type_freq <- data.frame(table(houses$type.new)) # 绘图 type_p <- ggplot(data = type_freq, mapping = aes(x = reorder(Var1, -Freq),y = Freq)) + geom_bar(stat = ‘identity‘, fill = ‘steelblue‘) + theme(axis.text.x = element_text(angle = 30, vjust = 0.5)) + xlab(‘户型‘) + ylab(‘套数‘) type_p
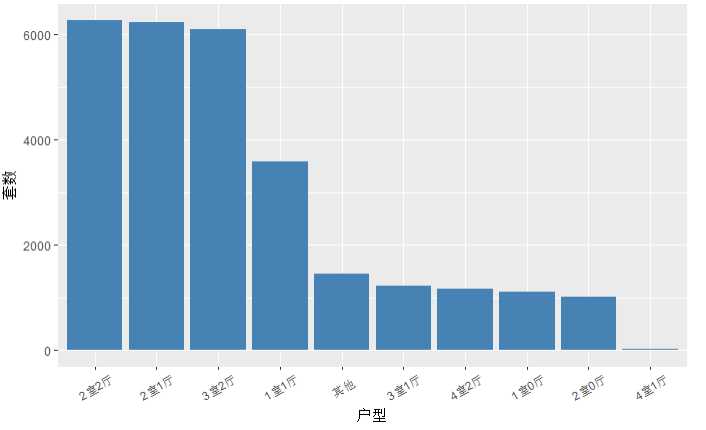
结论:2室2厅,2室1厅,3室2厅是上海比较多的二手房户型
6.楼层数据清洗
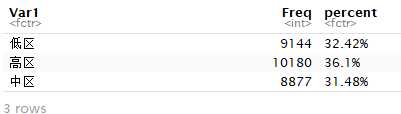
# 新建floor变量,使用ifelse来判断具体的楼层 houses$floor <- ifelse(substring(houses$楼层,1,2) %in% c(‘低区‘,‘高区‘,‘中区‘),substring(houses$楼层,1,2),‘低区‘) # 计算百分比 percent <- paste(round(prop.table(table(houses$floor))*100,2),‘%‘,sep = ‘‘) df <- data.frame(table(houses$floor)) df <- cbind(df,percent)
df
7.建筑时间清洗
# 自定义众数函数 stat.mode <- function(x, rm.na = TRUE){ if (rm.na == TRUE){ y = x[!is.na(x)] } res = names(table(y))[which.max(table(y))] return(res) } # 自定义函数,实现分组替补 my.impute <- function(data, category.col = NULL, miss.col = NULL, method = stat.mode){ impute.data = NULL for(i in as.character(unique(data[,category.col]))){ sub.data = subset(data, data[,category.col] == i) sub.data[,miss.col] = impute(sub.data[,miss.col], method) impute.data = c(impute.data, sub.data[,miss.col]) } data[,miss.col] = impute.data return(data) } # 将建筑时间中空白字符串转换为缺失值 houses$建筑时间[houses$建筑时间 == ‘‘] <- NA #分组替补缺失值,并对数据集进行变量筛选 final_house <- subset(my.impute(houses, ‘区域‘, ‘建筑时间‘),select = c(type.new,floor,面积,价格.W.,单价.平方米.,建筑时间)) #构建新字段builtdate2now,即建筑时间与当前2016年的时长 final_house <- transform(final_house, builtdate2now = 2016-as.integer(substring(as.character(建筑时间),1,4))) #删除原始的建筑时间这一字段 final_house <- subset(final_house, select = -建筑时间)
8.查看房价和面积的正态分布
# 自定义正态分布的函数 # 自定义绘图函数 norm.test <- function(x, breaks = 20, alpha = 0.05, plot = TRUE){ if(plot == TRUE) {#设置图形界面(多图合为一张图) opar <- par(no.readonly = TRUE) layout(matrix(c(1,1,2,3),2,2,byrow = TRUE), width = c(2,2),heights = c(2,2)) #绘制直方图 hist(x, freq = FALSE, breaks = seq(min(x), max(x), length = breaks), main = ‘x的直方图‘, ylab = ‘核密度值‘) #添加核密度图 lines(density(x), col = ‘red‘, lty = 1, lwd = 2) #添加正态分布图 x <- x[order(x)] lines(x, dnorm(x, mean(x), sd(x)), col = ‘blue‘, lty = 2, lwd = 2.5) #添加图例 legend(‘topright‘, legend = c(‘核密度曲线‘,‘正态分布曲线‘), col = c(‘red‘,‘blue‘), lty = c(1,2), lwd = c(2,2.5), bty = ‘n‘) #绘制Q-Q图 qqnorm(x, xlab = ‘实际分布‘, ylab = ‘正态分布‘, main = ‘x的Q-Q图‘, col = ‘blue‘) qqline(x) #绘制P-P图 P <- pnorm(x, mean(x), sd(x)) cdf <- 0 for(i in 1:length(x)){cdf[i] <- sum(x <= x[i])/length(x)} plot(cdf, P, xlab = ‘实际分布‘, ylab = ‘正态分布‘, main = ‘x的P-P图‘, xlim = c(0,1), ylim = c(0,1), col = ‘blue‘) abline(a = 0, b = 1) par(opar) } #定量的shapiro检验 if (length(x) <= 5000) { shapiro <- shapiro.test(x) if(shapiro$p.value > alpha) print(paste(‘定量结果为:‘, ‘x服从正态分布,‘, ‘P值 =‘,round(shapiro$p.value,5), ‘> 0.05‘)) else print(paste(‘定量结果为:‘, ‘x不服从正态分布,‘, ‘P值 =‘,round(shapiro$p.value,5), ‘<= 0.05‘)) shapiro } else { ks <- ks.test(x,‘pnorm‘) if(ks$p.value > alpha) print(paste(‘定量结果为:‘, ‘x服从正态分布,‘, ‘P值 =‘,round(ks$p.value,5), ‘> 0.05‘)) else print(paste(‘定量结果为:‘, ‘x不服从正态分布,‘, ‘P值 =‘,round(ks$p.value,5), ‘<= 0.05‘)) ks } }
# 面积的正态检验 norm.test(houses$面积)
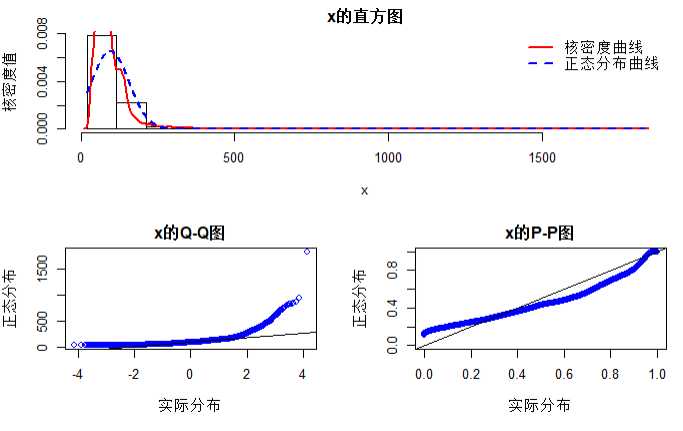
# 价格的正态检验 norm.test(houses$价格.W.)
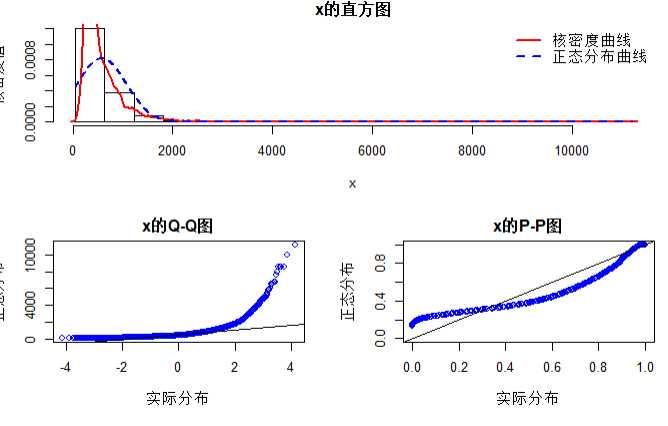
结论:房价和面积均不服从正态分布,因此不能对其进行做线性回归模型
9.查看上海地区二手房的均价
avg_price <- aggregate(houses$单价.平方米.,by=list(houses$区域),FUN=mean) p <- ggplot(data=avg_price,aes(x=reorder(Group.1,-x),y=x,group=1))+ geom_area(fill=‘lightgreen‘)+ geom_line(colour = ‘steelblue‘, size = 2)+ geom_point()+ ylab(‘均价‘) p
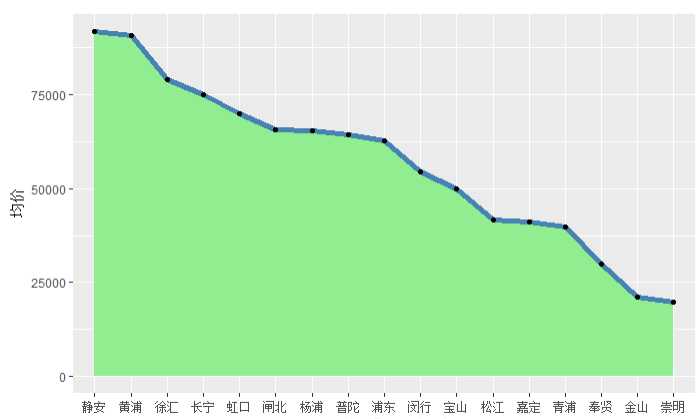
结论:静安区和徐汇区的价格较高
10.模型构建
在对房屋进行建模的时候,首先使用聚类把不同类型的房子给划分出来,我选择面积,房价,单价/㎡来进行聚类的划分
10.1 聚类的个数
# 模型构建 tot.wssplot <- function(data,nc,seed=1234){ # 计算距离的平方和 tot.wss <- (nrow(data)-1) * sum(apply(data,2,var)) for(i in 2:nc){ set.seed(seed) tot.wss[i] <- kmeans(data,centers = i,iter.max = 100)$tot.withinss } plot(1:nc,tot.wss,type=‘b‘,xlab = ‘Number of Cluster‘, ylab = ‘Within groups sum of squares‘,col=‘blue‘,lwd=2, main=‘choose best clusters‘) } # 找出判断聚类的三个主要的指标 stander <- data.frame(scale(final_house[,c(‘面积‘,‘价格.W.‘,‘单价.平方米.‘)])) # 做出聚类个数图 tot.wssplot(stander,15)
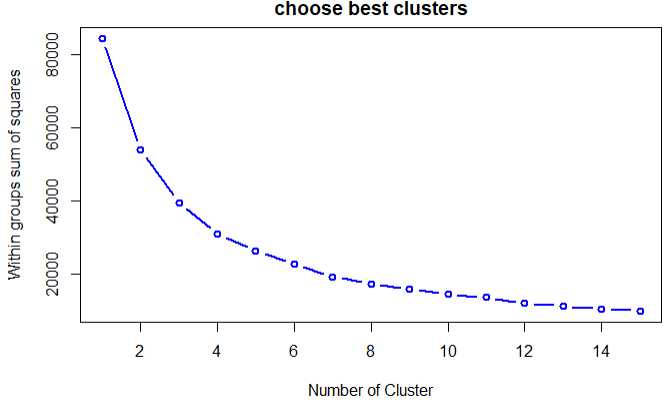
结论:分成5个类的模型的效果会比较好
10.2聚类
set.seed(1234) clust <- kmeans(x=stander,centers = 5,iter.max = 100)
table(clust$cluster)
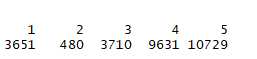
结论:每个聚类的结果
10.3查看聚类的结果
# 查看每个户型的平均面积 aggregate(final_house$面积,list(final_house$type.new),FUN=mean)

# 比较每个类中的面积,单价,每平米价格 aggregate(final_house[,3:5],list(clust$cluster),FUN=mean)

结论:
第1组是地段型的房子,地段位于上海的核心区域,每平米的单价是最高的
第2组是面积型的房子,地段稍逊于第1组,面积都在350平米以上,属于享受阶层买得起的房子
第3组是均衡型的房子,地段和面积均属于发展中的状态,房价涨势稳定,将来的发展空间较大
第4组是廉价型的房子,面积和价格都相对比较低,地段和面积相对较低
10.4聚类的散点图
p <- ggplot(data=final_house[,3:5],aes(x=面积,y=单价.平方米.,color=factor(clust$cluster)))+ geom_point(pch=20,size=3)+ scale_color_manual(values = c(‘red‘,‘blue‘,‘green‘,‘black‘,‘orange‘)) p
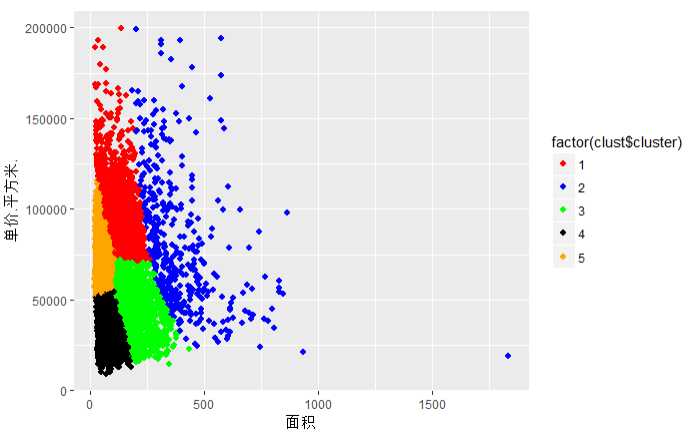
11建模
11.1 将类别变量变成因子类型
final_house$floor <- factor(final_house$floor) final_house$type.new <- factor(final_house$type.new) final_house$clsuter <- factor(clust$cluster)
11.2构建公式
# 选择出所有的因子变量 factors <- names(final_house)[sapply(final_house, class)==‘factor‘] formal <- f <- as.formula(paste(‘~‘,paste(factors,collapse = ‘+‘))) dummy <- dummyVars(formula = formal,data=final_house) pred <- predict(dummy,newdata=final_house) head(pred)
11.3建模
final_house2 <- cbind(final_house,pred) # 选择需要建模的因子 model_data <- subset(final_house2,select=-c(1,2,3,8,17,18,24)) fit1 <- lm(价格.W. ~ .,data=model_data) summary(fit1)
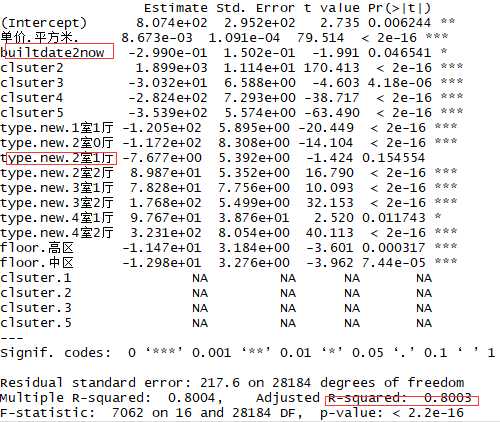
结论:建造时间和2室1厅的影响不明显,需要对模型进行修改
11.4修改模型
#由于房价不符合正态分布,所以要对价格取对数 powerTransform(fit1) fit2 <- lm(log(价格.W.) ~ .,data=model_data) summary(fit2)
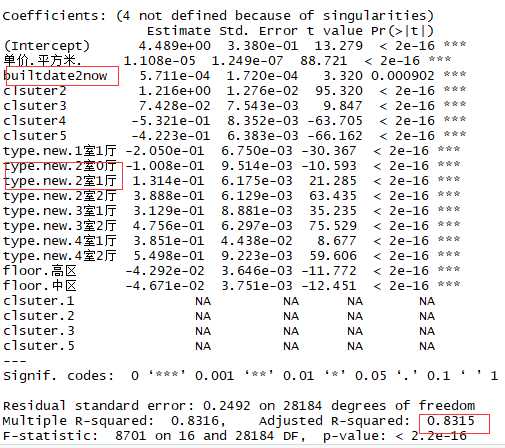
结论:R2的值得到了提高,并且建造时间和2室1厅的影响已经计入到模型中去
11.5查看最终模型的诊断结果
opar <- par(no.readonly = TRUE) par(mfrow = c(2,2)) plot(fit2) par(opar)
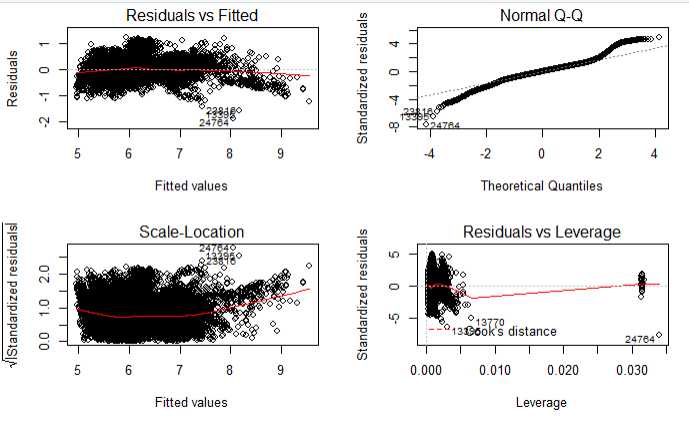
结论:符合线性回归模型的假设
