kmp算法详解
1、暴力匹配(BF算法)
假设有一文本串s,和一个模式串p,查找p在s中的位置?
用暴力匹配思路解决,假设文本s串匹配到i位置,模式串p匹配到j位置,则:
- 若 s[i] == p[j] ,则 i++,j++,继续匹配;
- 若 s[i] !=p[j],则令 i = i - (j - 1),即匹配失败 i 回溯,j 重置为 0。
代码如下:
int ViolentMatch(char* s, char* p) { int sLen = strlen(s); int pLen = strlen(p); int i = 0; int j = 0; while (i < sLen && j < pLen) { if (s[i] == p[j]) { //如果当前字符匹配成功(即S[i] == P[j]),则i++,j++ i++; j++; } else { //如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0 i = i - j + 1; j = 0; } } //匹配成功,返回模式串p在文本串s中的位置,否则返回-1 if (j == pLen) return i - j; else return -1; }
2、KMP算法
2.1、KMB算法思路及代码
用KMP算法思路解决,假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,则;
- 若 j == -1,或 s[i] == p[j] ,则 i++,j++,继续匹配;
- 若 j!= -1,且 s[i] !=p[j],则令 i = i - (j - 1),则令 i 不变, j = next[j] 。即,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值(移动的实际位数为:j - next[j])
代码如下:
int KMPMatch(char* s, char* p) { int i = 0; int j = 0; int sLen = strlen(s); int pLen = strlen(p); while (i < sLen && j < pLen) { //如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++ if (j == -1 || s[i] == p[j]) { i++; j++; } else { //如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j] // 即,字符失配,模式串跳到next [j] 的位置 j = next[j]; } } if (j == pLen) return i - j; else return -1; }
2.2next数组推导
next 数组各值的含义:代表当前字符之前的字符串中,有多大长度的相同前缀后缀。即,next [j] = k,代表j 之前的字符串中有最大长度为k 的相同前缀后缀。
- 前缀后缀最长公共元素长度
- 前缀max = 后缀 max,此时的长度
- 例如,模式串为abcabd,前缀后缀最大公共元素表,如下:

对于串abcab来说,它有最大长度为2的相同前缀后缀ab。
- next数组是由前缀后缀最长公共元素长度推导而来
- 即,j 指针所指字符之前的串的前缀后缀最长公共元素的长度 = next[j]
- 如例,模式串为abcabd,next数组值,如下:

对于字符d来说,它的前面的串为abcab,对于串abcab来说,它有最大长度为2的相同前缀后缀ab,所以d对应的next值为2。
以上两个表格的比较

可以发现,next值为前缀后缀最长公共元素长度求得的值整体右移一位,然后初值赋为-1。
2.3 根据next数组进行匹配
next数组的作用:当模式串中的某个字符跟文本串中的某个字符匹配失配时,告诉模式串下一步应该跳到哪个位置。如,模式串中在j 处的字符跟文本串在i 处的字符匹配失配时,下一步用next [j] 处的字符继续跟文本串i 处的字符匹配。
- 基于前缀后缀最大公共元素长度值的匹配
- 失配时,模式串向右移动的位数为:已匹配字符数 - 失配字符的上一位字符所对应的最大长度值
- 基于next值的匹配
- 失配时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值
简单总结,当从0开始计数时,失配字符的位置 = 已经匹配的字符数,而失配字符对应的next 值 = 失配字符的上一位字符的最大长度值。
2.4 next数组的代码推导
可以根据数学归纳法推导:
- 初始化 next[0] = -1;
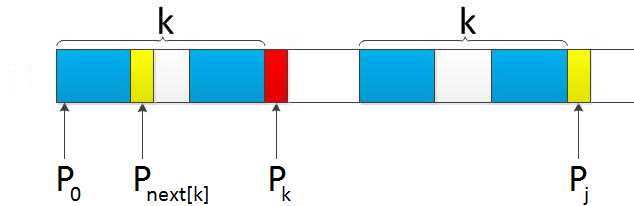
- 对于值k,已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1,相当于next[j] = k,即,代表p[j] 之前的模式串子串中,有长度为k 的相同前缀和后缀。
- 求解 next[j + 1] =? 分两种情况讨论:
-
- 若p[k] == p[j],则next[j + 1 ] = next [j] + 1 = k + 1 ;
- 若p[k] != p[j],则说明p[j + 1] 之前的模式串子串中,不存在长度为k + 1 的相同前缀后缀,只能去寻找长度更短一点的相同前缀后缀,即,令 k = next[k]进行递归;
- 若 p[k] = = p[j],next[j + 1] = k +1 (说明,此时k的值已经更新,即,k = next[k]);
- 若 p[k] ! = p[j],则递归。
代码如下:
void getNext(char *p, int * &next) { next = (int *)malloc(strlen(p) * sizeof(int)); if (!next) exit(-1); int j = 0; int k = -1; next[0] = -1; while (j < strlen(p) - 1){ //p[k]表示前缀,p[j]表示后缀 if(k == -1 || p[j] == p[k]){ next[++j] = ++k; }else{ k = next[k]; } } }
2.5 next数组的优化
根据next数组的代码推导,我们会发现,代码并没有对p[next[j]] == p[j]进行优化处理。
- next[j] = k;
- p[next[j]] == p[j](p[k] ==p[j])------------>next[j + 1] = k +1;(原先的next函数处理方式)
- p[next[j]] == p[j](p[k] ==p[j])------------>next[j ] = next[j] = next[next[j]] (k = next[k]);(优化后处理方式)
比如,如果用之前的next 数组方法求模式串“abab”的next 数组,可得其next 数组为-1 0 0 1(0 0 1 2整体右移一位,初值赋为-1),当它跟下图中的文本串去匹配的时候,发现b跟c失配,于是模式串滑动到next[3] = 1的位置,即,右移j - next[j] = 3 - 1 =2位。
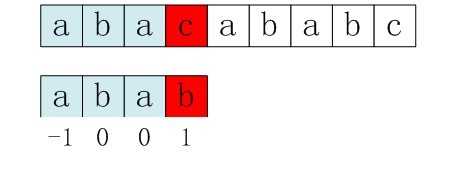
右移2位后,b又跟c失配。事实上,因为在上一步的匹配中,已经得知p[3] = b,与s[3] = c失配,而右移两位之后,让p[ next[3] ] = p[1] = b 再跟s[3]匹配时,必然失配。
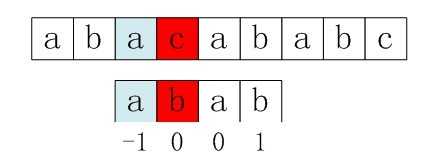
所以不应该出现p[next[j]] == p[j],如果出现了,则需要再次递归,即令next[j] = next[ next[j] ]。
优化后next数组求模式串“abab”的next 数组,可得其next 数组为-1 0 -1 1。
如上例,s[3] 和 p[3] 匹配失败后,s[3]保持不变,p的下一个匹配位置是p[next[3]],而next[3]=0,所以p[next[3]]=p[0]与s[3]匹配,
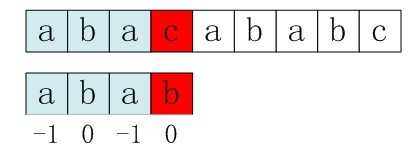
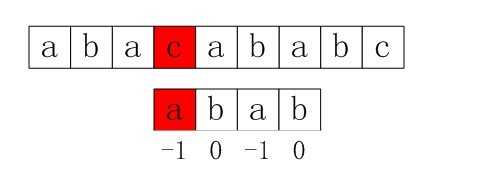
匹配成功
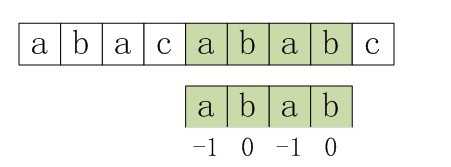
优化代码如下:
void getNext(char *p, int * &next) { next = (int *)malloc(strlen(p) * sizeof(int)); if (!next) exit(-1); int j = 0; int k = -1; next[0] = -1; while (j < strlen(p) - 1){ if(k == -1 || p[j] == p[k]){ if(p[++j] == p[++k]){ //不能出现p[j] == p[next[j]],如果出现,需要继续递归 next[j] = next[k]; }else{ next[j] = k; } }else{ k = next[k]; } } }
附完整代码:
#include <stdio.h> #include <stdlib.h> #include <string.h> int KMPMatch(char * s, char * p, int *next); void getNext(char * p, int * &next); int main() { int *next; char strtxt[200]; printf("请输入你的正文:\n"); gets(strtxt); char strkey[20]; printf("请输入你要查找的子串:\n"); gets(strkey); getNext(strkey, next); printf("子串的next求值结果:\n"); for (unsigned int i = 0; i <= strlen(strkey) - 1; ++i) { printf("%5c", strkey[i]); } printf("\n"); for (unsigned int i = 0; i <= strlen(strkey) - 1; ++i) { printf("%5d", next[i]); } printf("\n"); int pos = KMPMatch(strtxt, strkey, next); if (pos != -1) printf("字符匹配,匹配点是%d\n", pos); else printf("字符失配!\n"); system("pause"); return 0; } int KMPMatch(char * s, char * p, int *next){ int i = 0; int j = 0; int slen = strlen(s); int plen = strlen(p); while (i < slen && j < plen){ if(j == -1 || s[i] == p[j]){ i++; j++; }else{ j = next[j]; } } if(j == plen) return i - plen; else return -1; } void getNext(char *p, int * &next){ next = (int *)malloc(strlen(p) * sizeof(int)); if (!next) exit(-1); int j = 0; int k = -1; next[0] = -1; while (j < strlen(p) - 1){ if(k == -1 || p[j] == p[k]){ if(p[++j] == p[++k]){ next[j] = next[k]; }else{ next[j] = k; } }else{ k = next[k]; } } }
