标签:rate rgs bsp 包含 auto 特点 get 技术 初始
归并排序的核心操作,是将两个有序数组归并成一个更大的有序数组。
在这种思想下,通过递归的方式进行处理,就得到了归并排序。
首先我们写一个用来将两个有序数组归并(合并)为一个大数组的方法。
public static void MergeTwoArray(int[] a,int[] b,int[] c){
//a和b是两个有序的数组,c是a和b合并之后的有序数组
int i=0;//a的索引
int j=0;//b的索引
int k=0;//c的索引
while(i<a.length&&j<b.length){
if(a[i]<=b[j]){
c[k++]=a[i++];
}
else{
c[k++]=b[j++];
}
}
while(i<a.length){
c[k++]=a[i++];
}
while(j<b.length){
c[k++]=b[j++];
}
}
这就是归并(合并)的核心算法,比较容易理解。
现在我们调用一下这个方法:
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] a={1,3,5,7,9};
int[] b={0,2,4,6,8};
int[] c=new int[a.length+b.length];
MergeTwoArray(a,b,c);
for(int i=0;i<c.length;i++){
System.out.print(c[i]+" ");
}
}
输出的结果为:0 1 2 3 4 5 6 7 8 9
结果正确。这里需要传入三个数组作为参数,a和b是有序的子数组,c是合并之后的结果。那么在初始状态下,a和b都不是有序的,那要怎么办呢?
我们可以先对a和b进行排序。那使用哪种排序呢?之前我们已经介绍过三种排序方式:选择排序,插入排序,希尔排序。使用这三种方式,都可以对a和b先进行排序。然后再调用这个Merge方法,进行一次归并排序。
另外一种方式,就是对a和b也使用归并排序,也就是先分别对a和b都进行一次Merge调用。虽然这时候还无法立刻写出具体的实现,但是大概能想到这样一种结构:
public static void Merge(int[] x){
if(...){
return;
}
Merge(a‘);Merge(b‘);
MergeTwoArray(a‘,b‘,x)
}
这是一个伪代码,无法执行。但可以表达清楚这个方法的特点——递归调用。
递归最显著的特征就是,在一个方法中,调用自己。当然调用自己必须满足一些条件,否则容易出现死循环。
这个条件就是递归的终止条件。也就是上面代码中if(...)这个判断。
那么现在就要思考清楚,这个递归的终止条件是什么呢?
这是一个排序的方法,其主要的操作就是刚才我们说过的将两个有序数组合并为一个大的有序数组。那什么样的数组一定是有序的呢?这个问题听起来有点让人摸不着头脑,实际很简单——只有一个元素的数组,必定有序!因为,只有一个元素。
当然,也可以用其他的方式。比如,当一个子数组的长度小于某个值的时候,我们使用一次其他的排序方式进行排序,也可以达到相同的目的。
我们现在,考虑的是只有一个元素,调用归并排序的情形。这其实就是进行了一次比较大小。
假设我们当前有10个元素,待排序。那怎么才能使的它变成只有1个元素呢?
方法也有很多,比如每次取2个元素,索引0和1是一组,2和3是一组。。。依次类推。这样得到了很多个两元素的组合。将第一个元素当作a,第二个元素当作b,就可以进行一次排序。得到一个新的小数组c,它包含2个元素。
而第一组得到的包含2个元素的数组c1和第二组得到的包含2个元素的数组c2,又都是有序的子数组。就又可以进行一次排序。得到一个新的包含4个元素的数组。
按照这种思想,两个4元素的合并为1个8元素的,两个8元素的合并为1个16元素的。最终就达到了预期的长度。
但数组的长度不是2的次方,是怎么进行合并的呢?其实不用在意每个子数组在合并之前是否长度相同,只要有序就可以了。
我们以数组长度为10进行举例。
首先将它拆成两部分:前5项和后5项。
然后前5项再拆成两部分:前2后3(或者前3后2)。
然后前2项再拆成两部分:前1后1。
这是一棵二叉树的结构,最终每个叶子结点都只包含1个元素。
找一个16个元素的数组分解的二叉树图形:
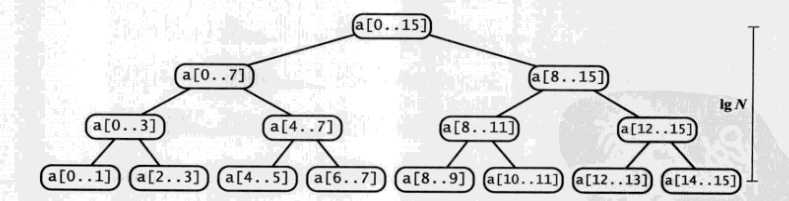
说了这么多,到底这个代码要怎么写呢?我现在按照刚才的描述,给出一段代码示例:
public static void Merge(int[] x){
if(x.length==1){
return;
}
int mid=x.length/2;
int k=0;
int[] a=new int[mid];
for(int i=0;i<a.length;i++){
a[i]=x[k++];
}
Merge(a);
int[] b=new int[x.length-mid];
for(int j=0;j<b.length;j++){
b[j]=x[k++];
}
Merge(b);
MergeTwoArray(a,b,x);
}
首先是要注意的是终止条件,当x.length==1时,不再进行递归。
如果x的元素数量大于1,则将其拆为两部分,两个子部分分别递归调用自己。
然后得到的a和b就是有序的数组了。这时再调用MergeTwoArray方法,就可以得到归并后的数组c。
再把c的值覆盖回原来的数组x,就完成了。
下面给出完整的代码:
package asen.yang;
public class mergeSort {
public static void main(String[] args) {
// TODO Auto-generated method stub
// int[] a={1,3,5,7,9};
// int[] b={0,2,4,6,8};
// int[] c=new int[a.length+b.length];
// MergeTwoArray(a,b,c);
// for(int i=0;i<c.length;i++){
// System.out.print(c[i]+" ");
// }
int[] x={9,7,5,3,1,8,6,4,2,0};
Merge(x);
for(int i=0;i<x.length;i++){
System.out.print(x[i]+" ");
}
}
public static void MergeTwoArray(int[] a,int[] b,int[] c){
//a和b是两个有序的数组,c是a和比合并之后的有序数组
int i=0;//a的索引
int j=0;//b的索引
int k=0;//c的索引
while(i<a.length&&j<b.length){
if(a[i]<=b[j]){
c[k++]=a[i++];
}
else{
c[k++]=b[j++];
}
}
while(i<a.length){
c[k++]=a[i++];
}
while(j<b.length){
c[k++]=b[j++];
}
}
public static void Merge(int[] x){
if(x.length==1){
return;
}
int mid=x.length/2;
int k=0;
int[] a=new int[mid];
for(int i=0;i<a.length;i++){
a[i]=x[k++];
}
Merge(a);
int[] b=new int[x.length-mid];
for(int j=0;j<b.length;j++){
b[j]=x[k++];
}
Merge(b);
MergeTwoArray(a,b,x);
}
}
除了这种实现,还有其他的实现方式,可以参考这篇文章:
http://www.cnblogs.com/asenyang/p/6915411.html
标签:rate rgs bsp 包含 auto 特点 get 技术 初始
原文地址:https://www.cnblogs.com/asenyang/p/8818520.html