零和数组

标签：turn   bsp   main   tps   自身   集合   test   情况   title   

题目：

长度为N的数组A中子数组和最接近0的子数组。

思路：

对于一个数组A，其子数组和最接近0只会出现在两种情况中：

1. 数组下标从 0 到 i 中
2. 数组下标从 i 到 j 中 
   （其中 i，j均小于数组长度）

如何做?

1. 对于第一种情况，只需要求出数组A从0带A.length所有前i项和，然后找出最小的。
2. 对于第二种情况，先求出 1 中所有前i项和，然后从小到大排序，最后将排序后的前i项和两两相减，取差值最小的
3. 最后取 1 和2 两种情况中最小者返回即可

申请同样长度的空间sum[0…N-1]，sum[i]是A的前i项和。 
? Trick：定义sum[-1] = 0 
? 显然有：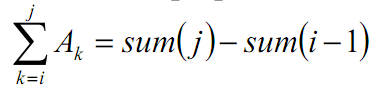  
? 算法： 
? 对sum[0…N-1]排序，然后计算sum相邻元素的差，最小值记为min1。 
? min1：在A中任意取两个集合，各自元素的和求差的最小值 
? 因为sum[-1]=0，sum[0…N-1]的绝对值最小值记为min2。 
? min2：A的前k个元素的和的绝对值的最小值 
? min1和min2的更小者，即为所求。

sum本身的计算和相邻元素差的计算，都是O(N)，sum的排序是O(NlogN)，因此，总时间复杂度：O(NlogN) 
强调：除了计算sum相邻元素的差的最小值，别忘了sum自身的最小值。 一个对应A[i…j]，一个对应A[0…j]

 1 ‘‘‘
 2 零和数组
 3 ‘‘‘
 4 
 5 
 6 def sums(a):
 7     n = len(a)
 8     sums = [0] * (n + 1)
 9     for i in range(0, n):
10         sums[i + 1] = sums[i] + a[i]
11     return sorted((sums[1:]))
12 
13 
14 def diff(a):
15     n = len(a)
16     d = [0] * (n - 1)
17     for i in range(1, n):
18         d[i - 1] = a[i] - a[i - 1]
19     return min(d)
20 
21 
22 def main(a):
23     a_sums = sums(a)
24     min_diff = diff(a_sums)
25     return min(min_diff, min(a_sums))
26 
27 test = [10, 14, 2, 3, -4]
28 print(main(test))

零和数组

标签：turn   bsp   main   tps   自身   集合   test   情况   title   

原文地址：https://www.cnblogs.com/zle1992/p/8859065.html