维基百科的解释是:在计算机科学中,Knuth-Morris-Pratt字符串查找算法(简称为KMP算法)可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始,从而避免重新检查先前已经匹配过的字符。
二、字符串的前缀与后缀
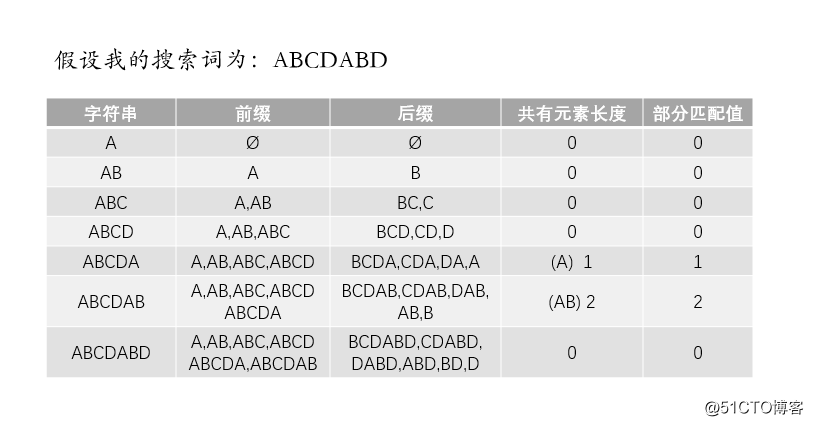
前缀:字符串除了最后一个字符的全部头部组合;
后缀:字符串处理第一个字符的全部头部组合;例如


三、字符串部分匹配表
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。所以我们需要找到一个字符串中每一个子串的匹配值,即找到字符串的部分匹配值表,这样的话我们在下面匹配字符串的过程中就可以根据匹配表来进行跳跃了,而不必一个一个字符往后移,这就是关键所在。
四、KMP算法实现过程
简单来说,KMP算法就是根据上面我们已经得到的部分匹配表来判断:匹配过程中发现子串的某个字符与待匹配串不对应时,子串应该往后移几位。
移动的位数 = 已经匹配成功的串的总长度 - 已经匹配成功的串的部分匹配值
有些绕,举个栗子,假如我要判断字符串"BBC ABCDAB ABCDABCDABDE"中是否含有串“ABCDABD”,我把前面这个长串叫做待匹配串,把“ABCDABD”叫做子串(有可能叫法不对但明白就行)。
匹配的过程为:
将字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。直到有匹配的字符位置,如下:

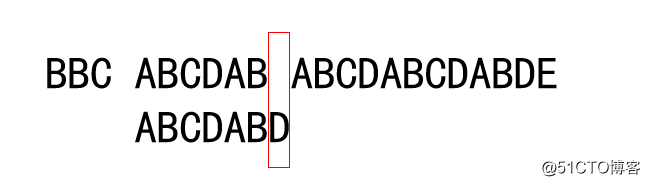
图中当匹配到D时发现不对应了,此时:
已经匹配成功的串为:ABCDAB
已经匹配成功的串的总长度:6
已经匹配成功的串的部分匹配值 :2
移动的位数 = 6 - 2,直接将子串往后移动4位,继续开始匹配

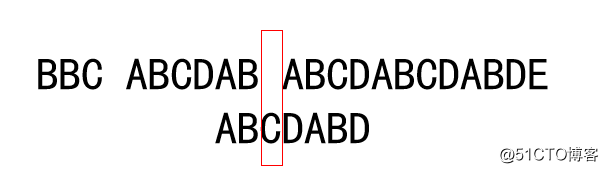
一样的道理,此时已经匹配成功的串为AB,移动的位数 = 2 - 0,往后移动2位继续匹配

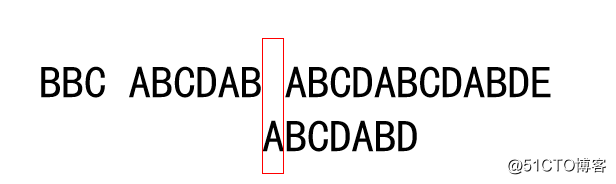
没有匹配成功的串,往后移一位


已经匹配成功的串为:ABCDAB,ABCDAB的部分匹配值为2,移动的位数 = 6 - 2,往后移动4位

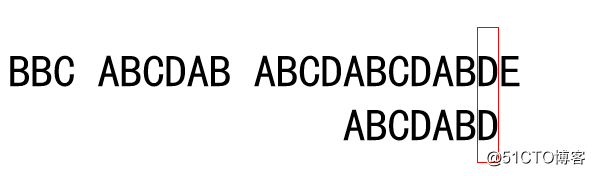
此时子串所有的字符都被匹配,搜索完成。
五、Java实现
public class KmpAlgo {
//寻找待匹配串的部分匹配值,放在next数组中
static void getNext(String pattern,int[] next){
int j = 0;
int k = -1;
next[0] = -1;
int len = pattern.length();
while(j < len-1){
if(k == -1 || pattern.charAt(j) == pattern.charAt(j)){
j++;
k++;
next[j] = k;
}else{
k = next[k];
}
}
}
static int kmp(String s,String pattern){
int i = 0;
int j = 0;
int slen = s.length();
int plen = pattern.length();
int[] next = new int[plen];
getNext(pattern,next);
while(i < slen && j < plen){
if(s.charAt(i) == pattern.charAt(j)){
i++;
j++;
}else if(next[j] == -1){
i++;
j = 0;
}else{
j = next[j];
}
if(j == plen){
return i-j;
}
}
return -1;
}
/**
*@param
*/
public static void main(String[] args){
String str = "ABCDABDEYGF";
String pat = "ABCDABD";
//KmpAlgo.kmp(str, pat);
System.out.println(KmpAlgo.kmp(str, pat));
}
}原文地址:http://blog.51cto.com/acevi/2104820