标签:隐藏 池化 它的 泛化 重叠 http 出现 信号 特征
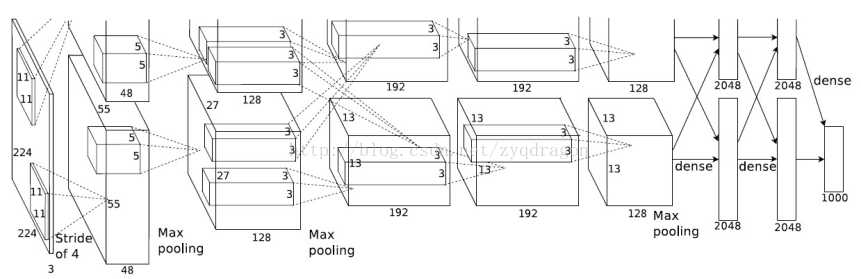
Alexnet是由5个卷积层和三个全连接层组成,一共8个权重层(池化层不是权重层因为其没有参数),其中ReLU激活函数作用在每个卷积层和全连接层上,在第一个卷积层和第二个卷积层后面连接一个局部响应规范化层,最大池化层作用在第一个卷积层,第二个卷积层和第五个卷积层的输出上。
在AlexNet结构中抛弃了传统的‘s‘形激活函数,而是选择了修正的线性单元作为激活函数也就是relu传统的’s‘形激活函数有f(x)=1/(1+e-x),f(x)=tanh(x),其中sigmoid函数如下图:
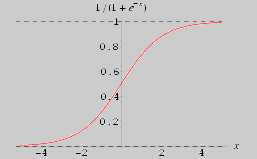
sigmoid函数具有饱和特性,当输入较大或者较小时,输出曲线接近平缓,此时梯度几乎为0,会造成消失的梯度问题,并且它的输出均值不为0,可能会造成偏置转移,会使得后一层的神经元将上一层的输出的非0均值的信号作为输入,并且它的输出范围在0~1,没有包含负信息,可能会损失一部分有用的信息。
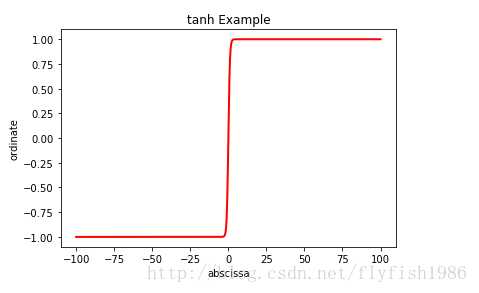
上图为tanh函数的曲线图,由图可知,它的输出值的范围为[-1,1],其输出均值为0,并且包含了负信息,但是由于它也具有饱和特性,所以也会造成消失的梯度问题。
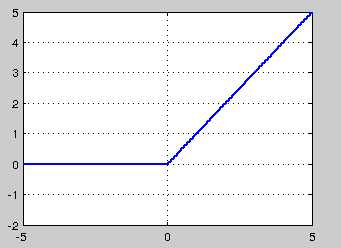
ReLU的形式为:f(x)=max(0,x),当输入为正时,输出值取其本身,此时关于输入x的导数为1,是一个常数,避免了消失的梯度问题,并且当输入小于0时,输出为0,引进了稀疏性,能够加速训练,但是由于其输出均值也大于0,所以也会出现偏置转移现象,并且由于当输入小于0时,对应的神经元输出为0,梯度为0,对应的权重也就无法更新。
AlexNet中使用了池化区域为3X3,步长为2的重叠池化,并且声称此种池化方法要比传统的池化区域为2X2,步长为2的非重叠池化方法效果好,论文中说效果提升了0.3%,但是我在其他数据集实验发现,重叠池化的效果不如非重叠池化,理由是当使用重叠池化时,下一个池化区域的最大值很可能就是上一个池化区域最大元素的副本,此时相当于造成了特征冗余。
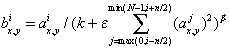
其中aix,y为第i个卷积核在位置(x,y)处做卷积得到特征映射中的元素,再使用relu对其进行非线性变化得到的神经元。bix,y为经过局部响应规范化处理后得到的神经元。N是在某一层中卷积核的总量.k,ε,n,β为超参数,由网络训练得到,在AlexNet中设置k=2,n=5,ε=10-4,β=0.75。局部响应规范化中的求和是在n个相邻的特征映射中的同一个位置,也就是(x,y),这样相当于在神经元之间引入一种竞争机制,较强的特征会有一个较大的元素值。
在图像数据中最简单和最普通减少过拟合的方法就是人工的扩增数据集,当然这是在保留标签信息的情况下。比如原图片的尺寸是256X256,就可以随机的在原图片上裁剪一个224X224的小块进行训练,并对其进行水平翻转,平移等操作,扩大数据集。
Dropout是一种正则化方法,随机的将隐藏层的神经元的值置为0,其中有一个drop率为p,通常p设置为0.5,dropout强迫每个神经元学习独立的特征,而不用依赖其他的神经元。它也相当于权重衰减,当某个神经元的值为0时,连接它的权重也为0,网络的参数变少,复杂度降低,防止过拟合,并且它也相当于一种模型融合,假设网络中一共有n个神经元,p=0.5,则此时,相当于有2n个子网络同时训练,是一种模型平均方法,提高泛化表现。
通常在卷积层后面都应该接一个池化层,但是AlexNet却只在第一个卷积层,第二个卷积层和最后一个卷积层后面连接最大池化,这是因为在网络的较低层,特征映射的大小一般很大,含有较多的参数,这是进行池化的目的是为了减少的参数的数量,防止过拟合,而在网络的较高层,提取的特征一般是高级特征,可能是某个物体的轮廓,比如小狗的眼睛,但是小狗可能出现在图像中的任意位置,此时最大池化的目的是提供一种平移翻转不变性。至于AlexNet为什么只用了5个卷积层,文中提到深度是重要的,但是再深可能会出现退化现象。而去掉一个卷积层又会使网络的表示能力下降。
标签:隐藏 池化 它的 泛化 重叠 http 出现 信号 特征
原文地址:https://www.cnblogs.com/czy4869/p/8890490.html