标签:技术 条件 line class 要求 举例 分解 order .com
本节内容
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
一个算法应该具有以下七个重要的特征:
①有穷性(Finiteness):算法的有穷性是指算法必须能在执行有限个步骤之后终止;
②确切性(Definiteness):算法的每一步骤必须有确切的定义;
③输入项(Input):一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输 入是指算法本身定出了初始条件;
④输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。没 有输出的算法是毫无意义的;
⑤可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行 的操作步,即每个计算步都可以在有限时间内完成(也称之为有效性);
⑥高效性(High efficiency):执行速度快,占用资源少;
⑦健壮性(Robustness):对数据响应正确。
计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间,时间复杂度常用大O符号(大O符号(Big O notation)是用于描述函数渐进行为的数学符号。更确切地说,它是用另一个(通常更简单的)函数来描述一个函数数量级的渐近上界。在数学中,它一般用来刻画被截断的无穷级数尤其是渐近级数的剩余项;在计算机科学中,它在分析算法复杂性的方面非常有用。)表述,使用这种方式时,时间复杂度可被称为是渐近的,它考察当输入值大小趋近无穷时的情况。
大O,简而言之可以认为它的含义是“order of”(大约是)。
无穷大渐近
大O符号在分析算法效率的时候非常有用。举个例子,解决一个规模为 n 的问题所花费的时间(或者所需步骤的数目)可以被求得:T(n) = 4n^2 - 2n + 2。
当 n 增大时,n^2; 项将开始占主导地位,而其他各项可以被忽略——举例说明:当 n = 500,4n^2; 项是 2n 项的1000倍大,因此在大多数场合下,省略后者对表达式的值的影响将是可以忽略不计的。
常数又称定数,是指一个数值不变的常量,与之相反的是变量
为什么下面算法的时间复杂度不是O(3),而是O(1)。
|
1
2
3
|
int sum = 0,n = 100; /*执行一次*/ sum = (1+n)*n/2; /*执行一次*/ printf("%d", sum); /*行次*/ |
这个算法的运行次数函数是f(n)=3。根据我们推导大O阶的方法,第一步就是把常数项3改为1。在保留最高阶项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为O(1)。
另外,我们试想一下,如果这个算法当中的语句sum=(1+n)*n/2有10句,即:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
int sum = 0, n = 100; /*执行1次*/ sum = (1+n)*n/2; /*执行第1次*/ sum = (1+n)*n/2; /*执行第2次*/ sum = (1+n)*n/2; /*执行第3次*/ sum = (1+n)*n/2; /*执行第4次*/ sum = (1+n)*n/2; /*执行第5次*/ sum = (1+n)*n/2; /*执行第6次*/ sum = (1+n)*n/2; /*执行第7次*/ sum = (1+n)*n/2; /*执行第8次*/ sum = (1+n)*n/2; /*执行第9次*/ sum = (1+n)*n/2; /*执行第10次*/ printf("%d",sum); /*执行1次*/ |
事实上无论n为多少,上面的两段代码就是3次和12次执行的差异。这种与问题的大小无关(n的多少),执行时间恒定的算法,我们称之为具有O(1)的时间复杂度,又叫常数阶。
注意:不管这个常数是多少,我们都记作O(1),而不能是O(3)、O(12)等其他任何数字,这是初学者常常犯的错误。
1.用常数1取代运行时间中的所有加法常数
2.在修改后的运行次数函数中,只保留最高阶项
3.如果最高阶项存在且不是1,则去除与这个项相乘的常数
对数
如果a的x次方等于N(a>0,且a不等于1),那么数x叫做以a为底N的对数(logarithm),记作x=logaN, 。其中,a叫做对数的底数,N叫做真数。
5^2 = 25 , 记作 2= log5 25
对数是一种运算,与指数是互逆的运算。例如
① 3^2=9 <==> 2=log<3>9;
② 4^(3/2)=8 <==> 3/2=log<4>8;
③ 10^n=35 <==> n=lg35。为了使用方便,人们逐渐把以10为底的常用对数记作lgN
对数阶
|
1
2
3
4
5
6
7
8
9
|
int count = 1;while (count < n){ count = count * 2; /* 时间复杂度为O(1)的程序步骤序列 */} |
由于每次count乘以2之后,就距离n更近了一分。
也就是说,有多少个2相乘后大于n,则会退出循环。
由2^x=n得到x=log2n。所以这个循环的时间复杂度为O(logn)。
执行时间随问题规模增长呈正比例增长
|
1
2
3
4
5
|
data = [ 8,3,67,77,78,22,6,3,88,21,2]find_num = 22for i in data: if i == 22: print("find",find_num,i ) |
|
1
2
3
4
|
for i in range(100): for k in range(100): print(i,k) |
立方阶O(n^3)
k次方阶O(n^k),
指数阶O(2^n)。
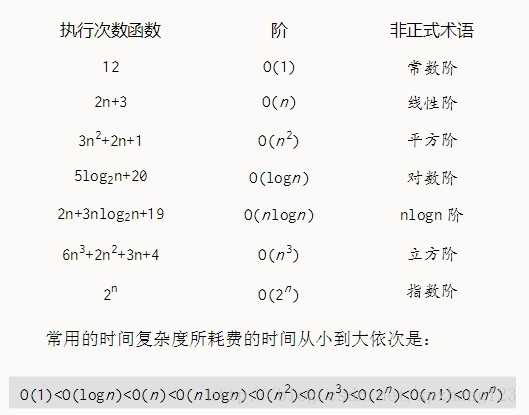
随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
标签:技术 条件 line class 要求 举例 分解 order .com
原文地址:https://www.cnblogs.com/adc8868/p/8926183.html