标签:tool strong 来源 定义 ast \n tps print rip
精确覆盖问题的定义:给定一个由0-1组成的矩阵,是否能找到一个行的集合,使得集合中每一列都恰好包含一个1。
例如:如下的矩阵
就包含了这样一个集合(第1、4、5行)。
采用回溯法
每一次枚举选择的行,可行则继续,若无论怎么选都不能再继续,回溯。
这里引用大佬的例子:
原址:https://www.cnblogs.com/grenet/p/3145800.html
矩阵1:
先假定选择第1行,如下所示:
如上图中所示,红色的那行是选中的一行,这一行中有3个1,分别是第3、5、6列。
由于这3列已经包含了1,故,把这三列往下标示,图中的蓝色部分。蓝色部分包含3个1,分别在2行中,把这2行用紫色标示出来
根据定义,同一列的1只能有1个,故紫色的两行,和红色的一行的1相冲突。
那么在接下来的求解中,红色的部分、蓝色的部分、紫色的部分都不能用了,把这些部分都删除,得到一个新的矩阵
矩阵2:
行分别对应矩阵1中的第2、4、5行
列分别对应矩阵1中的第1、2、4、7列
于是问题就转换为一个规模小点的精确覆盖问题
在新的矩阵中再选择第1行,如下图所示
还是按照之前的步骤,进行标示。红色、蓝色和紫色的部分又全都删除,导致新的空矩阵产生,而红色的一行中有0(有0就说明这一列没有1覆盖)。说明,第1行选择是错误的
那么回到之前,选择第2行,如下图所示
按照之前的步骤,进行标示。把红色、蓝色、紫色部分删除后,得到新的矩阵
行对应矩阵2中的第3行,矩阵1中的第5行
列对应矩阵2中的第2、4列,矩阵1中的第2、7列
由于剩下的矩阵只有1行,且都是1,选择这一行,问题就解决
于是该问题的解就是矩阵1中第1行、矩阵2中的第2行、矩阵3中的第1行。也就是矩阵1中的第1、4、5行
从上面的求解过程来看,实际上求解过程可以如下表示
1、从矩阵中选择一行
2、根据定义,标示矩阵中其他行的元素
3、删除相关行和列的元素,得到新矩阵
4、如果新矩阵是空矩阵,并且之前的一行都是1,那么求解结束,跳转到6;新矩阵不是空矩阵,继续求解,跳转到1;新矩阵是空矩阵,之前的一行中有0,跳转到5
5、说明之前的选择有误,回溯到之前的一个矩阵,跳转到1;如果没有矩阵可以回溯,说明该问题无解,跳转到7
6、求解结束,把结果输出
7、求解结束,输出无解消息
这样做的话就会遇到以下问题:
如何储存每一步的状态;
如何输出正确结果。
算法大师Donald E.Knuth提出的舞蹈链便是一种巧妙的解决方法。
我们都知道链表具有便于插入和删除的优点,
如:a,b,c顺次相连,
删除b: b.left.right = b.right, b.right.left = b.left;//即:a.right = c, c.left = a;没有改变b中的内容 再插入b: b.left.right = b.right.left = b; //即:a.right = b.left = b;可利用b中的内容
再看常规做法中的关键步骤——删除行(列) 和 插入(恢复)行(列),恰好可以利用这两点便利,不仅节省空间(因为不必每一步都重开矩阵),时间上效率也高。
Dancing Links 使用的是交叉十字循环双向链。
交叉:每一行一条(。。)链表,每一列再来一条(。。)链表。
由于我们只考虑覆盖那些行列,只关心为1的位置,所以将为1的位置存起来,
如下图所示:(一张著名的图。。)
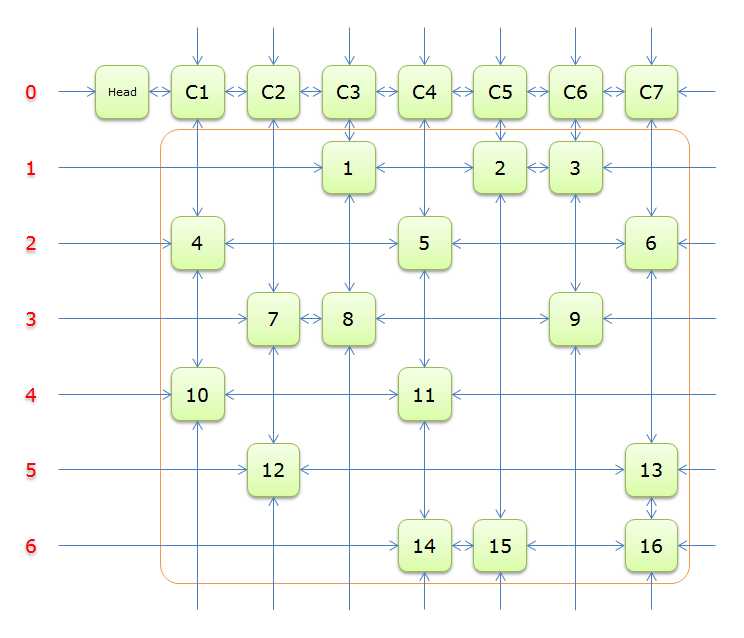
对应矩阵:
head和C1、C2……都是辅助元素:
head主要起到寻找未覆盖列和判定是否找到一种方案,head.right就是还未覆盖的某一列列标,head.right==head时表明所有列都已被覆盖。
C1、C2…可以看作列标,删除和恢复列都将从这里开始,同时也保证删除列后还能找到恢复列的“入口”。
所以可以定义结构体如下:
struct node
{
node *L, *R, *U, *D, *col;
int x;
node(node *a = 0, node *b = 0, node *c = 0, node *d = 0,
node *e = 0, int f = 0)
:L(a), R(b), U(c), D(d), col(e), x(f) {};
}其中, L,R,U,D分别指向左、右、上、下的元素,col指向所在行的列标元素,x是行号。
至于构造函数。。。纯粹是我乱搞的。。。。
考虑到精确覆盖问题的定义,我们的目标是覆盖所有列,所以每一次找到还未覆盖的一列进行操作。
假设我们找到了列标为c的一列,我们先假装要覆盖这一列。
首先就要删除这一列,而我们只需在行链表上删除列标即可,因为进入列都是通过列标实现的。然后不论我们选哪一行来覆盖,所有能覆盖这一列的行都不能再选了,于是这一列上每一个元素(除了列标)所在的行都要删除。但是,有可能会出现一种不妙的状况—— c->D == c, 即无法覆盖这一列!这时,就应该返回false表示决策错误了。如果成功删除了这一列,自然就返回true了。
代码如下:
bool remove(node *c)
{
c->L->R = c->R, c->R->L = c->L;
if (c->D == c) return false;
for (node *i = c->D; i != c; i = i->D)
for (node *j = i->R; j != i; j = j->R)
{
j->U->D = j->D;
j->D->U = j->U;
}
return true;
}删除行时也要注意保留“入口”,即第7行的:j = i->R 和 j != i。
恢复就相对简单一些了。
第一步:恢复该列相关的行;
第二步:恢复该列。
上代码:
void recover(node *c)
{
for (node *i = c->D; i != c; i = i->D)
for (node *j = i->R; j != i; j = j->R)
j->U->D = j->D->U = j;
c->L->R = c->R->L = c;
}主体部分主要是回溯的过程。
首先要找到未覆盖的列,head->right即是(见上文的“储存方式”一节),若head->right == head,说明找到解,返回true。
然后就是删除这一列,这时判断一下remove函数返回值,若为false可直接返回false表不可行。
成功删除列后,我们发现我们之前只删除了相关的行,没有真正地“选”哪一行,于是我们枚举一下选哪一行,并把这一行能覆盖的列都删除。做完这一工作,我们就可以继续处理剩下的未覆盖列了。
处理剩下的列我们依然调用主体函数,当它返回了true时,表明已经找到解,我们枚举的这一行当然也在解中,直接输出。否则,我们就要继续尝试选择另一行,在此之前,先恢复之前被我们删掉的行。
若枚举完所有行都没有可行解,返回false。
代码如下:
bool DLX()
{
node *c = head->R;
if (c == head) return true;
if (!remove(c)) return false;
for (node *i = c->D; i != c; i = i->D)
{
for (node *j = i->R; j != i; j = j->R)
remove(j->col);
if (DLX())
{
printf ("%d ", i->x);
return true;
}
for (node *j = i->R; j != i; j = j->R)
recover(j->col);
}
return false;
}如此,指针飞舞,大概就是Dancing Links名称的来源吧。
综合起来的代码(输出一组可行解):
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
struct node
{
node *L, *R, *U, *D, *col;
int x;
node(node *a = 0, node *b = 0, node *c = 0, node *d = 0,
node *e = 0, int f = 0)
:L(a), R(b), U(c), D(d), col(e), x(f) {};
}*head, *tail[100005];
int n, m;
bool remove(node *c)
{
c->L->R = c->R, c->R->L = c->L;
if (c->D == c) return false;
for (node *i = c->D; i != c; i = i->D)
for (node *j = i->R; j != i; j = j->R)
{
j->U->D = j->D;
j->D->U = j->U;
}
return true;
}
void recover(node *c)
{
for (node *i = c->D; i != c; i = i->D)
for (node *j = i->R; j != i; j = j->R)
j->U->D = j->D->U = j;
c->L->R = c->R->L = c;
}
bool DLX()
{
node *c = head->R;
if (c == head) return true;
if (!remove(c)) return false;
for (node *i = c->D; i != c; i = i->D)
{
for (node *j = i->R; j != i; j = j->R)
remove(j->col);
if (DLX())
{
printf ("%d ", i->x);
return true;
}
for (node *j = i->R; j != i; j = j->R)
recover(j->col);
}
return false;
}
int main()
{
head = new node();
scanf ("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
tail[i] = new node();
for (int i = 2; i < m; i++)
tail[i]->L = tail[i - 1], tail[i]->R = tail[i + 1];
for (int i = 1; i <= m; i++)
tail[i]->U = tail[i]->D = tail[i];
head->L = tail[m], head->R = tail[1], head->D = head->U = head;
tail[m]->L = tail[m - 1], tail[m]->R = head;
tail[1]->R = tail[2], tail[1]->L = head;
for (int i = 1; i <= n; i++)
{
node *last = NULL;
for (int j = 1; j <= m; j++)
{
int a;
scanf ("%d", &a);
if (a)
{
node *newnode = new node(NULL, NULL, tail[j], tail[j]->D, tail[j]->D, i);
tail[j]->D = tail[j]->D->U = newnode;
tail[j] = newnode;
if (!last) newnode->L = newnode->R = newnode;
else
{
newnode->L = last, newnode->R = last->R;
last->R = last->R->L = newnode;
}
last = newnode;
}
}
}
if (!DLX())
printf ("No solution!\n");
return 0;
}由于奇特的代码风格,代码有点宽,恳请勿喷。。。标签:tool strong 来源 定义 ast \n tps print rip
原文地址:https://www.cnblogs.com/Rhein-E/p/8969773.html