标签:了解 并且 sign exti integer 表达式计算 练习 analysis 工作
在一个人孤身奋斗了将近半个学期以后,终于迎来的我们的第一次团队协作共同编码,也就是,我们的第一个结对编程练习——四则运算。显然,他是考验我们对于之前知识的掌握程度,而且考验我们的能力,既然已经是一个结对编程练习,肯定存在着困难,但我们会迎难而上,一起解决问题,因为“团结就是力量!!!”
20172316 赵乾宸:负责对于整数出题的编程;
20172319 唐才铭:负责对于分数出题的编程;
我:20172329 王文彬:负责对于计算和题目去重的编写;
测试为分别进行测试,最后由赵乾宸进行集体测试。
每个人都是驾驶员,是彼此的引航员,团队,分工明确是一部分,但是集体力量的结晶才是最伟大的!!!
1、计算的最开始构思:
首先,当第一次拿到这个题目的时候,首先进行思考的是加减乘除的整个运算逻辑,因为当时没有了解过有后缀表示法,所以一直在想如何用中缀表达式开始计算; 一方面,思考的是输出的题目应该是字符串类型还是数据类型,后来想了想,各有各自的优点和缺点,比如,计算的时候的确,数字是很方便的,但是当涉及到计算的时候,遇到的“+”、“-”、“*”、“/”,几个符号就我现在的水平,没有办法去很好的解决,之后就想到了,假如将这几个运算符号进行改变,将其变为几个数字代表他们,不就可以了,最后有这样一个问题,如果用“0”来代表“+”,有一个问题,因为“+”是一个字符串,对其赋值还得进行强制转化,对于程本身这样其实是不利的,存在着一定的问题,所以,就先将计算问题放了放,开始想,如何出题;
2、开始出题:
最开始,还是以出题为主,考虑到“if-else”语句的复杂性,我们选择了“swich语句“,因为,这样可以进行人际互动,一方面可以实现我们所需要的输入一个阶数,可以完成对于该阶数的出题;构思是这样的,先利用对于符号的赋值,对于加减乘除四个符号进行对0123的赋值,以便于通过对于产生一个0~4(左闭右开)的一个随机数取值实现对于字符串的出题的随机性,将输出的符号给一个字符对象进行赋值,之后,开始在里面加入数字,如何解决阶数的控制,一方面,利用swich语句的方便,其次,利用了累加“+=”进行输出,就会产生按照我们需求的题目;另一方面,需要输出按照我们所敲入的数字进行题目个数的输出,我们想到了运用数组和while语句,这样,按照条件,输出数组,就可以达到我们想要的一个结果,也就是一个理想的出题模型。
protected int a;
protected String s1 = "", str = "";
public Compute2() {
Scanner scan = new Scanner(System.in);
System.out.println("几级运算?");
int n = scan.nextInt();
Scanner qqq = new Scanner(System.in);
System.out.println("生成几个题目?");
int q = qqq.nextInt();
Object[] p = new Object[q] ;
for (int index = 0; index < q; index++) {
int a1 = (int) (Math.random() * 100);
int a2 = (int) (Math.random() * 100);
int t1 = (int) (Math.random() * 4);
switch (t1) {
case 0: {
s1 = " + ";
break;
}
case 1: {
s1 = " - ";
break;
}
case 2: {
s1 = " * ";
break;
}
case 3: {
s1 = " / ";
}
}
for (int i = 0; i < n - 1; i++) {
int a = (int) (Math.random() * 100);
int t = (int) (Math.random() * 4);
String s = "";
switch (t) {
case 0: {
s = " + ";
break;
}
case 1: {
s = " - ";
break;
}
case 2: {
s = " * ";
break;
}
case 3: {
s = " / ";
}
}
str += a + s;
}
str += a1 + s1 + a2;
p[index]=str;3、学习从中缀表达式到后缀表达式的变化:
在课上,学习了解了后缀表达式,这个表达式方便了我们进行计算代码的编写,利用了“栈”这个概念,在思考运算的过程中简化了很多步骤;
在利用栈解决问题的时候有一个问题:就是假如是两位数,如何去解决,这个问题在某一天的晚自习里,学长给我们就这个问题进行了讲解,利用StringTokenzer的方法进行对于字符串的分隔,这个方法可以将两个数字或者三个乃至三个以上的字符进行划分,让他们单独成为整体,这样就方便了我们的计算,就可以解决1234+不是123+4而是12+34的问题,感谢学长。
public String infixToSuffix() {
Stack<Character> s = new Stack<Character>();
String suffix = "";
int length = str.length(); for (int i = 0; i < length; i++) {
char temp;// 临时字符变量
char ch = str.charAt(i);
switch (ch) {
case ' ':
break;
case '(':
s.push(ch);
break;
case '+':
case '-':
while (s.size() != 0) {
temp = s.pop();
if (temp == '(') {
s.push('(');
break;
}
suffix += temp;
}
s.push(ch);
break;
case '*':
case '/':
while (s.size() != 0) {
temp = s.pop();
if (temp == '+' || temp == '-' || temp == '(') {
s.push(temp);
break;
} else {
suffix += temp;
}
}
s.push(ch);
break;
case ')':
while (!s.isEmpty()) {
temp = s.pop();
if (temp == '(') {
break;
} else {
suffix += temp;
}
}
break;
default:
suffix += ch;
break;
}
}
while (s.size() != 0) {
suffix += s.pop();
} return suffix;4、在出题过程中去重问题上的思考:
如何去重,一方面,我们想到的是只要是结果相同的就是相同的,后来,发现并不是这样简单的,因为,在看了老师的博客中所介绍的:
程序一次运行生成的题目不能重复,即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。例如,23 + 45 = 和45 + 23 = 是重复的题目,6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的,由于+是左结合的,1+2+3等价于(1+2)+3,也就是3+(1+2),也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题,因为1+2+3等价于(1+2)+3,而3+2+1等价于(3+2)+1,它们之间不能通过有限次交换变成同一个题目。
看到了如此的要求,就开始进行思考;
5、计算问题:(我是负责这里部分编写的)
在遇见计算的时候,主要靠的就运用后缀表达式的方法,利用栈进行计算,大概思路如下:
public Integer suffixToArithmetic() {
Pattern pattern = Pattern.compile("\\d+||(\\d+\\.\\d+)");
String[] strings = str.split("");
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < strings.length; i++) {
if (strings[i].equals("")) {
continue;
}
if (pattern.matcher(strings[i]).matches()) {
stack.push((int) Double.parseDouble(strings[i]));
}
else {
double y = stack.pop();
double x = stack.pop();
stack.push((int) calculate(x, y, strings[i]));
}
}
return stack.pop();
}
private double calculate(double x, double y, String string) {
if (string.trim().equals("+")) {
return x + y;
}
if (string.trim().equals("-")) {
return x - y;
}
if (string.trim().equals("*")) {
return x * y;
}
if (string.trim().equals("/")) {
return x / y;
}
return (double) 0;
}

转后缀:
第一个问题:
如何去解决出题过程中如何去添加括号,因为括号的位置的不确定性就限制了我们如何去选择,比如,假如出现像加法和乘法混在一起,括号应该选择加在加法位置?
解决方案:
我们想要将加法和括号绑定在一起,之后利用swich语句判断,什么时候不需要在加法减法周围加括号,什么时候不需要加。
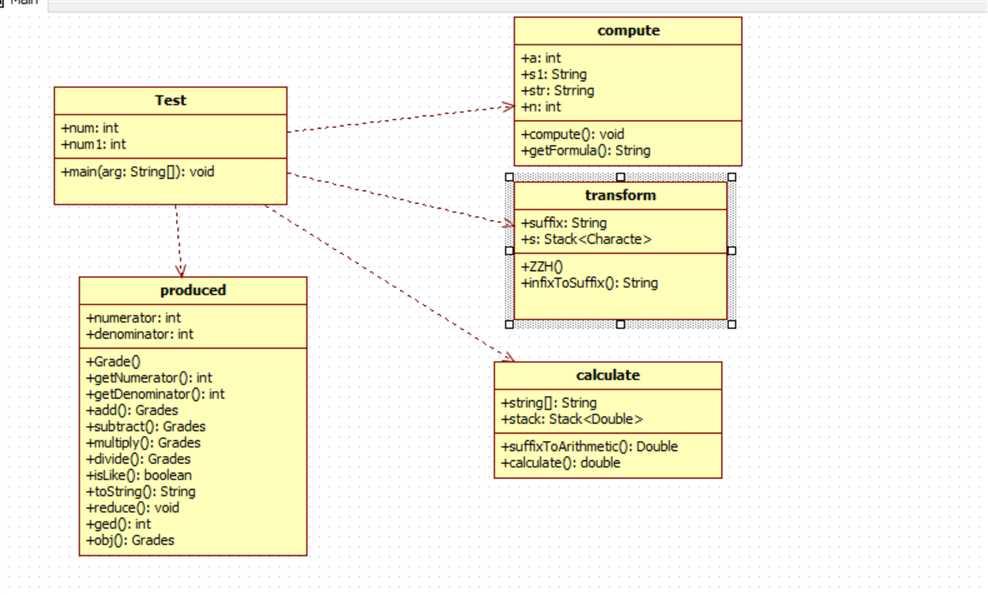
第二个问题:
因为我们是先进行了代码的编写,然后通过对于代码画UML图,所以现在就有以一个问题,因为一些代码命名不同,使得存在一些问题,(这个是我们组的失误,下次会纠正的)
解决方案:
现在正在汇总,之后打算统一为UML图的编码格式,然后对各自的代码进行修改。
20172316赵乾宸
小赵同学担起了开始编写代码的大任,在发布任务的第二天,因为我和老唐同学在连续的两天都有晚课,所以一开始,小赵同学的功劳功不可没,而且他是我们团队编程能力最强的,所以,我们都会向他看齐。
20172319唐才铭
老唐同学分配了我们的任务,并且也担起了团队的一遍大旗,为彼此加油鼓劲。
大家加油!!
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | |
| Estimate | 估计这个任务需要多少时间 | 100 | |
| Development | 开发 | 800 | |
| Analysis | 需求分析 (包括学习新技术) | 100 | |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 30 | |
| Design UML | 设计项目UML类图 | 50 | |
| Coding | 具体编码 | 30 | |
| Code Review | 代码复审 | 50 | |
| Test | 测试(自我测试,修改代码,提交修改) | 30 | |
| Size Measurement | 计算工作量(实际时间 | 30 | |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 30 | |
| 合计 | 1240 |
Java堆栈的应用2----------中缀表达式转为后缀表达式的计算Java实现
用java实现复数的加减乘除运算
逆波兰表达式
表达式计算 java 后缀表达式
Java实现中缀表达式转后缀表达式并计算结果
2017-2018-2 1723 『Java程序设计』课程 结对编程练习-四则运算-准备阶段
标签:了解 并且 sign exti integer 表达式计算 练习 analysis 工作
原文地址:https://www.cnblogs.com/qh45wangwenbin/p/8973616.html