标签:输出 路径 sid height 并且 string span namespace type
1)普里姆算法
可取图中任意一个顶点v作为生成树的根,之后若要往生成树上添加顶点w,则在顶点v和顶点w之间必定存在一条边,并且
该边的权值在所有连通顶点v和w之间的边中取值最小。一般情况下,假设n个顶点分成两个集合:U(包含已落在生成树上
的结点)和V-U(尚未落在生成树上的顶点),则在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。
例如:起始生成树上面就一个顶点。为了连通两个集合,在可选的边中,选择权值最小的。需要辅助数组,V-U中所有顶点。
具体实例如下图所示:求下图的最小生成树
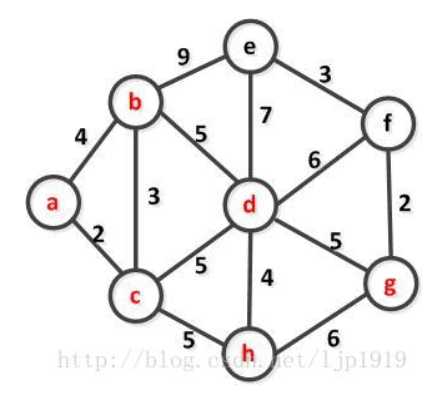
我们以a点为起始点,此时的U集合={a},V-U到U集合的路径有a-b=4,a-c=2,取最小的a-c,所以将c点添加到U集合中,U={a,c}。
此时,V-U到U集合的路径有b-a=4,b-c=3,取最小,更新b点到U集合的最短路径为3,此外还有c-d=5,c-h=5,所以,取V-U到U集
合的最小值为b-c=3,将b点添加到U集合中。U={a,c,b}。此时V-U到U集合存在以下点:c-d=5,c-h=5,b-d=5(与现有的c-d=5一样,
所以不更新,仍旧采用c-d),b-e=9,取最小的,此时可以有两个选择,假设选择c-d,所以将d点添加到U集合中。U={a,c,b,d}。
此时V-U到U的路径,因为e-d=7<e-b=9,所以e点进行更新,更新为d-e=7;同理d-h=4<c-h=5,所以点h到U的路径更新为d-h=4。
新增加的路径为d-f和d-g。此时选择V-U到U集合的最短路径为d-h=4,所以将h添加到U集合,此时U={a,c,b,d,h}。依次不断选择
下一个距离U集合最短路径的点,并将其添加到U集合,直到将所以顶点添加完毕。实现过程如下图所示:
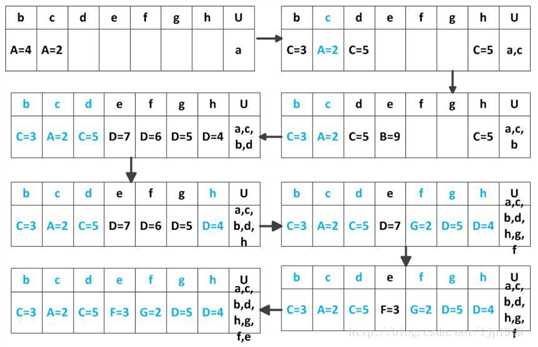
接下来的代码示例图:
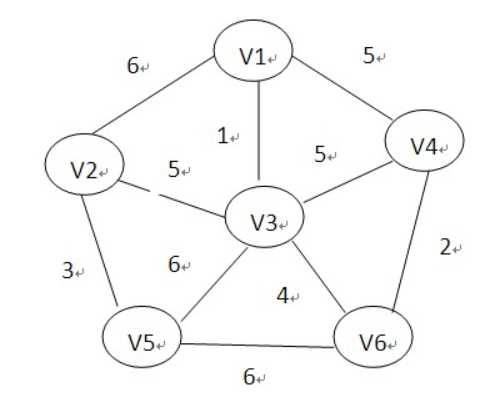
代码如下:
1 #include "stdafx.h" 2 #include<iostream> 3 #include<string> 4 using namespace std; 5 6 #define MaxNum 10000 7 typedef struct MGraph 8 { 9 string vexs[60]; 10 int arcs[100][100]; 11 int vexnum, arcum; 12 }MGraph; 13 typedef struct Closedge 14 { 15 string adjvex; 16 int lowcost; 17 }minside[100]; 18 19 int locateVex(MGraph G, string u) //返回顶点u在图中的位置 20 { 21 for (int i = 0; i < G.vexnum; i++) 22 if (G.vexs[i] == u) 23 return i; 24 return -1; 25 } 26 27 void CreateGraphUDG(MGraph &G) //构造无向图 28 { 29 string v1, v2; 30 int w; 31 int i, j, k; 32 cout << "请输入顶点数和边数:"; 33 cin >> G.vexnum >> G.arcum; 34 35 cout << "请输入顶点:"; 36 for (i = 0; i < G.vexnum; i++) 37 cin >> G.vexs[i]; 38 39 for (i = 0; i < G.vexnum; i++) 40 for (j = 0; j < G.vexnum; j++) 41 G.arcs[i][j] = 10000; 42 43 cout << "请输入边和权值:" << endl; 44 for (k = 0; k < G.arcum; k++) 45 { 46 cin >> v1 >> v2 >> w; 47 i = locateVex(G, v1); 48 j = locateVex(G, v2); 49 G.arcs[i][j] = G.arcs[j][i] = w; 50 } 51 52 } 53 54 int minimum(minside sz, MGraph G) //求sz中lowcost的最小值,返回序号 55 { 56 int i = 0, j, k, min; 57 while (!sz[i].lowcost) 58 i++; 59 min = sz[i].lowcost; 60 k = i; 61 for (j = i + 1; j < G.vexnum; j++) 62 { 63 if (sz[j].lowcost > 0 && min > sz[j].lowcost) 64 { 65 min = sz[j].lowcost; 66 k = j; 67 } 68 } 69 return k; 70 } 71 72 void MiniSpanTree_PRIM(MGraph G, string u) //普里姆算法 73 { 74 int i, j, k; 75 minside closedge; 76 k = locateVex(G, u); 77 for (j = 0; j < G.vexnum; j++) 78 { 79 closedge[j].adjvex = u; 80 closedge[j].lowcost = G.arcs[k][j]; 81 } 82 closedge[k].lowcost = 0; 83 cout << "最小生成树各边为:" << endl; 84 85 for (i = 1; i < G.vexnum; i++) 86 { 87 k = minimum(closedge, G); 88 cout << closedge[k].adjvex << "-" << G.vexs[k] << endl; 89 closedge[k].lowcost = 0; 90 for (j = 0; j < G.vexnum; j++) 91 { 92 if (G.arcs[k][j] < closedge[j].lowcost) 93 { 94 closedge[j].adjvex = G.vexs[k]; 95 closedge[j].lowcost = G.arcs[k][j]; 96 } 97 } 98 } 99 } 100 101 int main() 102 { 103 MGraph G; 104 CreateGraphUDG(G); 105 MiniSpanTree_PRIM(G, G.vexs[0]); 106 cout << endl; 107 return 0; 108 }
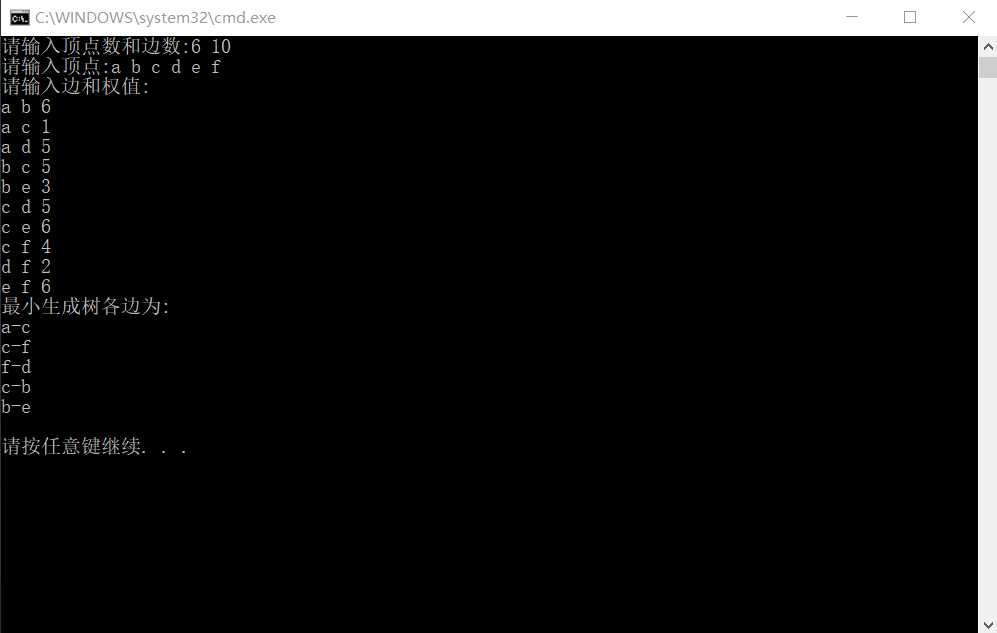
输出结果:
关于克鲁斯卡尔算法博主明天会更新,请耐心等待...
标签:输出 路径 sid height 并且 string span namespace type
原文地址:https://www.cnblogs.com/Trojan00/p/8983207.html