标签:oid integer stat nbsp -- height 实现 数字 pre
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如,输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于这个数字2在数组中出现了5次,超过数组长度的一半,因此输出2.
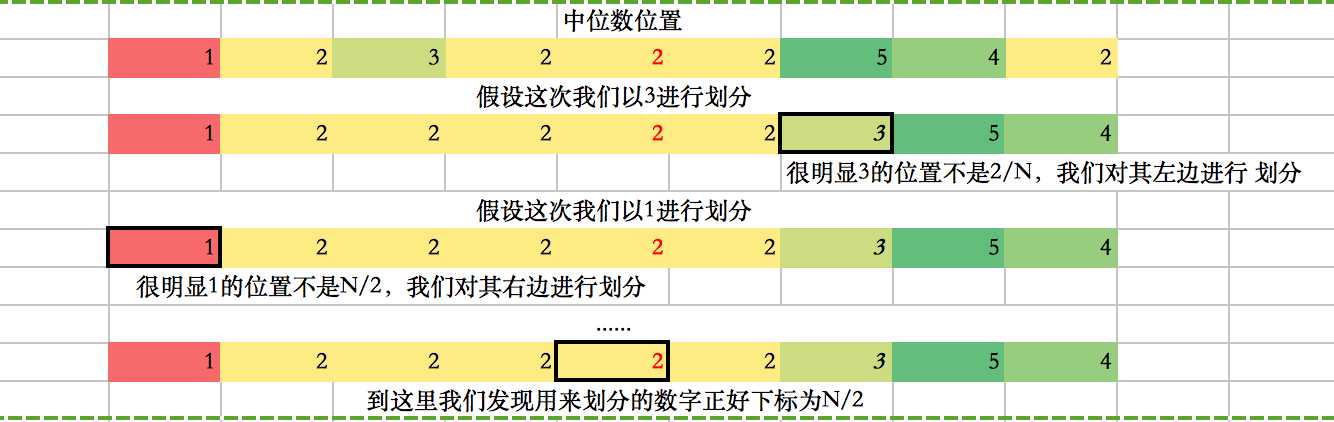
数组中有一个数字出现的次数超过了数组长度的一半。如果把这个数组排序,那么排序之后位于数组中间的数字一定就是那个出现次数超过数组长度一半的数字。也就是说,这个数字就是统计学上的中位数。
在随机快排算法中,我们现在数组中随机选择一个数字,然后调整数组中数字的顺序,使得比选中的数字小的数字都在它的左边,比选中数字大的数字都排在它的右边。如果选中的这个数字的小标刚好是n/2,那么这个数字就是这个数字的中位数;如果它的下标大于n/2,那么中位数应该位于它的左边,我们可以接着在它的左边部分的数组中进行查找。否则,可以在右边中进行查找!
大概意思是这样的:
import java.util.Scanner;
public class PartitionDemo {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
String str = input.nextLine();
String[] arrStr =str.split(" ");
int[] arrN = new int[arrStr.length];
for(int i=0;i<arrStr.length;i++)
arrN[i]= Integer.parseInt(arrStr[i]);
System.out.println(MoreThanHalfNum(arrN,arrN.length));
}
//数目超过一半的数字
public static int MoreThanHalfNum(int[] numbers,int length)
{
int middle = length>>1;
int start = 0;
int end = length-1;
int index = partition(numbers,start,end);
while (index!=middle)
{
if(index>middle) {
end = index-1;
index = partition(numbers,start,end);
}
else{
start = index+1;
index=partition(numbers,start,end);
}
}
int result = numbers[middle];
return result;
}
//划分
public static int partition(int[] aux,int lo,int hi)
{
int i=lo,j=hi+1; //左右两个指针,分别从两端开始
int val = aux[lo]; //取最左边的第一个元素为枢纽元素
while (true)
{
while (aux[++i]<val)if(i==hi)break; //左指针向右找到一个大于枢纽的
while (aux[--j]>val)if(j==lo)break; //右指针向左找到一个大于枢纽的
if(i>=j) break; //这个i>=j是很关键的,这表明现在已经划分成功,即两边元素有序!
exch(aux,i,j); //i!=j,表示还有能找的!
}
exch(aux,lo,j); //把枢纽元素交换至它应该的位置!
return j; //把划分点返回区,目的是说,从这里开始,两边分别已成为为左右子序列,返回的是j这是很关键的,因为i可能大于j。
}
//交换
public static void exch(int[] aux,int i,int j)
{
int t=aux[i];
aux[i]=aux[j];
aux[j]=t;
}
}
标签:oid integer stat nbsp -- height 实现 数字 pre
原文地址:https://www.cnblogs.com/MrSaver/p/9047911.html