标签:selection UI max 取出 get blog span java实现 info
本文使用Java实现这几种排序。
以下是对排序算法总体的介绍。
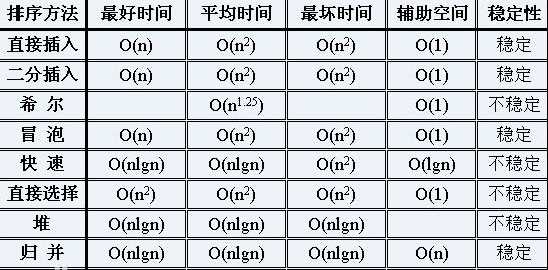
时间复杂度:O(n^2),最优时间复杂度:O(n),平均时间复杂度:O(n^2)

1public static void bubbleSort(Comparable[] a) { 2 int j, flag; 3 Comparable temp; 4 for (int i = 0; i < a.length; i++) { 5 flag = 0; 6 for (j = 1; j < a.length - i; j++) { 7 if (a[j].compareTo(a[j - 1]) < 0) { 8 temp = a[j]; 9 a[j] = a[j - 1]; 10 a[j - 1] = temp; 11 flag = 1; 12 } 13 } 14 // 如果没有交换,代表已经排序完毕,直接返回 15 if (flag == 0) { 16 return; 17 } 18 } 19}
时间复杂度:O(n^2),最优时间复杂度:O(n),平均时间复杂度:O(n^2)

下面展示了三种插入排序的实现,第二种方法减少了交换次数,第三种采用二分查找法查到插入点。
1public static void insertionSort(Comparable[] a) { 2 int length = a.length; 3 Comparable temp; 4 for (int i = 1; i < length; i++) { 5 for (int j = i; j > 0 && a[j].compareTo(a[j - 1]) < 0; j--) { 6 temp = a[j]; 7 a[j] = a[j - 1]; 8 a[j - 1] = temp; 9 } 10 } 11} 12 13// 对实现Comparable的类型进行排序,先将大的元素都向右移动,减少一半交换次数 14public static void insertionSort(Comparable[] a) { 15 int length = a.length; 16 Comparable temp; 17 int j; 18 for (int i = 1; i < length; i++) { 19 temp = a[i]; 20 for (j = i; j > 0 && temp.compareTo(a[j - 1]) < 0; j--) { 21 a[j] = a[j - 1]; 22 } 23 a[j] = temp; 24 } 25} 26 27// 二分插入排序,使用二分查找找到插入点,然后进行移位 28public static void insertionSort(Comparable[] a) { 29 int length = a.length; 30 Comparable temp; 31 int j; 32 for (int i = 1; i < length; i++) { 33 if (a[i].compareTo(a[i - 1]) < 0) { 34 temp = a[i]; 35 int index = binarySearch(a, a[i], 0, i - 1); 36 for (j = i - 1; j >= index; j--) { 37 a[j + 1] = a[j]; 38 } 39 a[index] = temp; 40 } 41 } 42} 43 44private static int binarySearch(Comparable[] a, Comparable target, int start, int end) { 45 int mid; 46 while (start <= end) { 47 mid = (start + end) >> 1; 48 if (target.compareTo(a[mid]) < 0) { 49 end = mid - 1; 50 } else { 51 start = mid + 1; 52 } 53 } 54 return start; 55}
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
时间复杂度:O(n^2),最优时间复杂度:O(n^2),平均时间复杂度:O(n^2)

1public static void selectionSort1(Comparable[] a) { 2 int length = a.length; 3 int min; 4 Comparable temp; 5 for (int i = 0; i < length; i++) { 6 min = i; 7 for (int j = i + 1; j < length; j++) { 8 if (a[j].compareTo(a[min]) < 0) { 9 min = j; 10 } 11 } 12 temp = a[min]; 13 a[min] = a[i]; 14 a[i] = temp; 15 } 16}
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
时间复杂度:根据步长而不同,最优时间复杂度:O(n),平均时间复杂度:根据步长而不同
1public static void shellSort(Comparable[] a) { 2 int length = a.length; 3 int h = 1; 4 Comparable temp; 5 while (h < length / 3) { 6 h = 3 * h + 1; 7 } 8 while (h >= 1) { 9 for (int i = h; i < length; i++) { 10 for (int j = i; j >= h && a[j].compareTo(a[j - h]) < 0; j -= h) { 11 temp = a[j]; 12 a[j] = a[j - h]; 13 a[j - h] = temp; 14 } 15 } 16 h /= 3; 17 } 18}
时间复杂度:O(nlogn),最优时间复杂度:O(nlogn),平均时间复杂度:O(nlogn)
1public static void heapSort(Comparable[] a) { 2 int length = a.length; 3 Comparable temp; 4 for (int k = length / 2; k >= 1; k--) { 5 sink(a, k, length); 6 } 7 while (length > 0) { 8 temp = a[0]; 9 a[0] = a[length - 1]; 10 a[length - 1] = temp; 11 length--; 12 sink(a, 1, length); 13 } 14} 15 16private static void sink(Comparable[] a, int k, int n) { 17 Comparable temp; 18 while (2 * k <= n) { 19 int j = 2 * k; 20 if (j < n && a[j - 1].compareTo(a[j]) < 0) { 21 j++; 22 } 23 if (a[k - 1].compareTo(a[j - 1]) >= 0) { 24 break; 25 } 26 temp = a[k - 1]; 27 a[k - 1] = a[j - 1]; 28 a[j - 1] = temp; 29 k = j; 30 } 31}
归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
时间复杂度:O(nlogn),最优时间复杂度:O(n),平均时间复杂度:O(nlogn),空间复杂度O(n)

自顶向下的归并排序 1private static Comparable[] aux; 2// 自顶向下 3public static void mergeSort(Comparable[] a) { 4 aux = new Comparable[a.length]; 5 mergeSort(a, 0, a.length - 1); 6} 7 8public static void mergeSort(Comparable[] a, int lo, int hi) { 9 if (hi <= lo) { 10 return; 11 } 12 int mid = (lo + hi) >>> 1; 13 mergeSort(a, lo, mid); 14 mergeSort(a, mid + 1, hi); 15 merge(a, lo, mid, hi); 16} 17 18public static void merge(Comparable[] a, int lo, int mid, int hi) { 19 int i = lo, j = mid + 1; 20 21 for (int k = lo; k <= hi; k++) { 22 aux[k] = a[k]; 23 } 24 25 for (int k = lo; k <= hi; k++) { 26 if (i > mid) { 27 a[k] = aux[j++]; 28 } else if (j > hi) { 29 a[k] = aux[i++]; 30 } else if (aux[j].compareTo(aux[i]) < 0) { 31 a[k] = aux[j++]; 32 } else { 33 a[k] = aux[i++]; 34 } 35 } 36} 自底向上的归并排序 1private static Comparable[] aux; 2 3// 自底向上 4public static void mergeSort(Comparable[] a) { 5 int length = a.length; 6 aux = new Comparable[length]; 7 for (int sz = 1; sz < length; sz = sz + sz) { 8 for (int lo = 0; lo < length - sz; lo += sz + sz) { 9 merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, length - 1)); 10 } 11 } 12} 13 14public static void merge(Comparable[] a, int lo, int mid, int hi) { 15 int i = lo, j = mid + 1; 16 17 for (int k = lo; k <= hi; k++) { 18 aux[k] = a[k]; 19 } 20 21 for (int k = lo; k <= hi; k++) { 22 if (i > mid) { 23 a[k] = aux[j++]; 24 } else if (j > hi) { 25 a[k] = aux[i++]; 26 } else if (aux[j].compareTo(aux[i]) < 0) { 27 a[k] = aux[j++]; 28 } else { 29 a[k] = aux[i++]; 30 } 31 } 32}
时间复杂度:O(n^2),最优时间复杂度:O(nlogn),平均时间复杂度:O(nlogn)
快排的时间复杂度跟选取基准的方法有关,一下是默认选择了第一个元素作为基准,随机性较大。
可以在序列中选取开始中间结尾三个数的中位数作为基准,进行优化。
1public static void quickSort(Comparable[] a) { 2 quickSort(a, 0, a.length - 1); 3} 4 5public static void quickSort(Comparable[] a, int lo, int hi) { 6 if (hi <= lo) { 7 return; 8 } 9 int j = partition(a, lo, hi); 10 quickSort(a, lo, j - 1); 11 quickSort(a, j + 1, hi); 12} 13 14public static int partition(Comparable[] a, int lo, int hi) { 15 int i = lo, j = hi + 1; 16 Comparable temp; 17 Comparable v = a[lo]; 18 while (true) { 19 while (a[++i].compareTo(v) < 0) { 20 if (i == hi) { 21 break; 22 } 23 } 24 while (v.compareTo(a[--j]) < 0) { 25 if (j == lo) { 26 break; 27 } 28 } 29 if (i >= j) { 30 break; 31 } 32 temp = a[i]; 33 a[i] = a[j]; 34 a[j] = temp; 35 } 36 temp = a[lo]; 37 a[lo] = a[j]; 38 a[j] = temp; 39 return j; 40}
---恢复内容结束---
原文地址:http://www.cnblogs.com/Tanyboye/p/9054170.html
标签:selection UI max 取出 get blog span java实现 info
原文地址:https://www.cnblogs.com/vlsion/p/9056989.html