标签:解决 ini 循环 图片 占用 重要 排序 过多 空间
知识内容:
1.递归复习
2.常用算法
3.常用数据结构
4.python cookbook算法与数据结构整理
参考资料:
http://python3-cookbook.readthedocs.io/zh_CN/latest/index.html
http://www.cnblogs.com/alex3714/articles/5474411.html
一、递归复习
1.什么是递归:函数内部自己调用自己
2.递归的特点
3.看函数说结果
1 def func1(x): 2 print(x) 3 func1(x-1) 4 func1(5) 5 # 一直打印到限制次数(无出口) 6 7 def func2(x): 8 if x > 0: 9 print(x) 10 func2(x+1) 11 func2(5) 12 # 一直打印到限制次数(无出口) 13 14 def func3(x): 15 if x > 0: 16 print(x) 17 func3(x-1) 18 func3(5) 19 # 从5打印到1 20 21 def func4(x): 22 if x > 0: 23 func4(x-1) 24 print(x) 25 func4(5) 26 # 从1打印到5
4.经典递归
(1)汉诺塔问题
解决思路:
假设有n个盘子:
1:
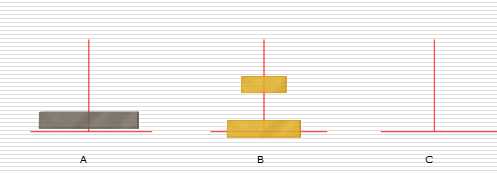
2:
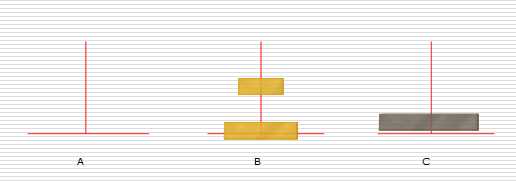
3:
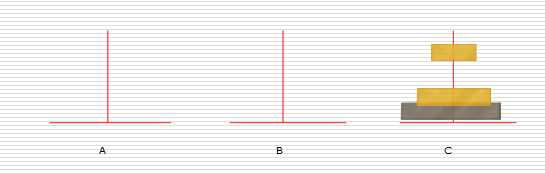
代码:
1 def hanoi(a, b, c, n): 2 if n == 1: 3 print(a, "->", c) # 将n-1个盘子从a经过c移动到b 4 else: 5 hanoi(a, c, b, n-1) # 将剩余的最后一个盘子从a移动到c 6 print(a, "->", c) 7 hanoi(b, a, c, n-1) # 将n-1个盘子从b经过a移动到c 8 9 10 hanoi(‘柱子a‘, ‘柱子b‘, ‘柱子c‘, 4)
总结:汉诺塔移动次数的递推式:h(x)=2h(x-1)+1
(2)字符串逆序输出
1 def rvs(s): 2 if s == "": 3 return s 4 else: 5 return rvs(s[1:]) + s[0] 6 7 8 s = rvs("Hello, Python") 9 print(s)
5.尾递归
二、常用算法
1.什么是算法
算法就是一个计算过程,解决问题的方法
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量
一个算法应该具有以下七个重要的特征:
2.时间复杂度及空间复杂度
(1)时间复杂度
1 print("hello, world") 2 3 for i in range(n): 4 print("hello, world") 5 6 for i in range(n): 7 for j in range(n): 8 print("hello, world") 9 10 for i in range(n): 11 for j in range(n): 12 for k in range(n): 13 print("hello, world")
问以上代码的运行时间谁最短?用什么方法来提现代码(算法)的运行快慢呢?答案就是用时间复杂度来衡量
常见算法的时间复杂度(由小到大排列):O(1) O(logn) O(n) O(nlogn) O(n^2) O(n^2logn) O(n^3)
实例:
1 print(‘hello world‘) 2 print(‘hello python‘) # O(1) 大O,可以认为它的含义是“order of”(大约是) 3 4 n= 64 5 while n>1: 6 print(n) # O(logn) # n=64是输出依次为: 64 32 16 8 4 2 7 n = n//2 8 9 for i in range(n): 10 print(i) # O(n) 11 12 for i in range(n): 13 for j in range(n): 14 print(‘hello world‘) # O(n^2) 15 16 for i in range(n): 17 for j in range(n): 18 for k in range(n): 19 print(‘hello world‘) # O(n^3)
注:切片的复杂度是O(n) ,因为切的时候是赋值
总结:
(2)空间复杂度
空间复杂度是用来评估算法内存占用大小的一个式子,常见的空间复杂度:O(1) O(n) O(n^2)
空间换时间:计算机的资源很充足,可以用空间的消耗来换取一定的时间
3.常用查找
(1)列表查找
列表查找:从列表中查找指定元素
输入:列表、待查找的元素,输出:元素下标或未查找到元素
列表查找的方法:顺序查找和二分查找
以上两种查找的代码如下:
# 顺序查找 时间复杂 O(n) def linear_search(find, data_list): for i in range(len(data_list)): if data_list[i] == find: return i return -1 # 二分查找 时间复杂 O(logn) def binary_search(find, data_list): low = 0 high = len(data_list) while low <= high: mid = (low + high) // 2 # 找到find if data_list[mid] == find: return mid # find在左半边 elif data_list[mid] > find: high = mid - 1 # find在右半边 else: low = mid + 1 # 未找到find返回-1 return -1
(2)查找练习
现在有一个学员信息列表(按id增序排列),格式为:
1 [ 2 {"id": 1001, "name": "张三", "age": 20}, 3 {"id": 1002, "name": "woz", "age": 22}, 4 {"id": 1003, "name": "alex", "age": 23}, 5 {"id": 1004, "name": "hf", "age": 26}, 6 {"id": 1005, "name": "kk", "age": 27}, 7 ]
现在要求修改二分查找代码,输入学生id,输出该学生在该列表下的下标并输出完整的学生信息
实现代码如下:
4.常用排序
常用的排序有以下几种:
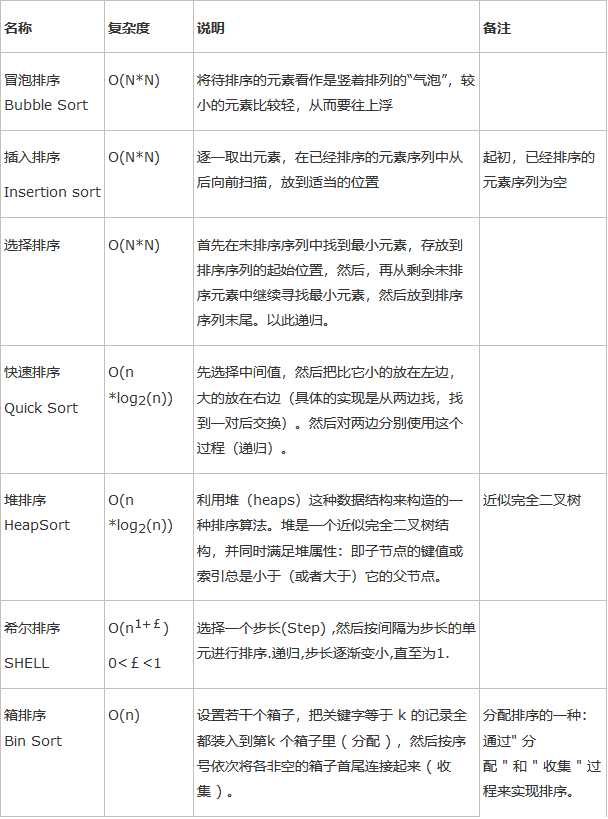
三、常用数据结构
四、python cookbook算法与数据结构整理
标签:解决 ini 循环 图片 占用 重要 排序 过多 空间
原文地址:https://www.cnblogs.com/wyb666/p/8990024.html