标签:输入 误差 str can TE lock rom ios size
1. 复化梯形法公式以及递推化
复化梯形法是一种有效改善求积公式精度的方法。将[a,b]区间n等分,步长h = (b-a)/n,分点xk = a + kh。复化求积公式就是将这n等分的每一个小区间进行常规的梯形法求积,再将这n的小区间累加求和。 公式如下:
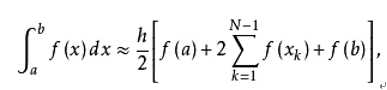
使用复化梯形法积分时,可以将此过程递推化,以更方便的使用计算机实现。设积分区间[a,b],将此区间n等分,则等分点共有n+1个,使用复化梯形积分求得Tn。进行二分,二分结果记为T2n,则有:
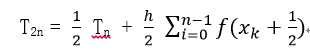
2. 龙贝格积分公式
龙贝格积分实际上是提高收敛速度的一种算法。由于复化梯形法步长减半后误差减少至 ,即有:
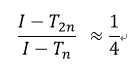
整理得:
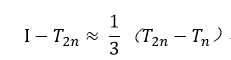
根据此思路,将收敛缓慢的梯形值序列Tn加工成收敛迅速的龙贝格值序列Rn,这就是龙贝格算法,加工算法流程如下:
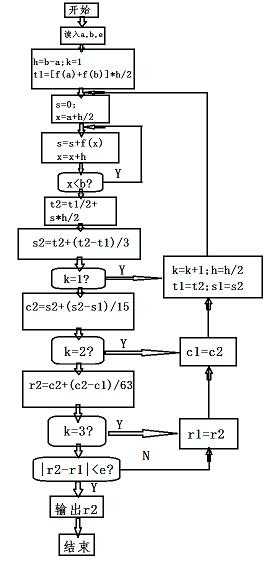
实现:
1 #include<stdio.h> 2 #include<math.h> 3 #include<iostream> 4 #include<cstdio> 5 using namespace std; 6 int Rk=0; 7 int Tk=0; 8 double fx(double x) //被积函数 9 { 10 //if(x==0.0)return 1.0; 11 return 3*x*x*x+2*x*x+1 + sin(x); 12 } 13 double getReal(double a,double b){ 14 double r1 = 3.0/4.0 * b*b*b*b + 2.0/3.0*b*b*b + b - cos(b); 15 double r2 = 3.0/4.0 * a*a*a*a + 2.0/3.0*a*a*a + a - cos(a); 16 return r1 - r2; 17 } 18 double getS(double a,double b,double h) 19 { 20 double res=0.0; 21 for(double i=a+h/2.0; i<b; i+=h){ 22 res+=fx(i); 23 } 24 25 return res; 26 } 27 double Romberg(double a,double b,double e) 28 { 29 int k=1; 30 double T1,T2,S1,S2,C1,C2,R1,R2; 31 double h=b-a; 32 double s; 33 T1=(fx(a)+fx(b))*h/2.0; 34 int counter=0; 35 while(1) 36 { 37 Rk++; 38 counter++; 39 s=getS(a,b,h); 40 T2=(T1+h*s)/2.0; 41 S2=(4.0*T2-T1)/3.0; 42 h/=2.0; 43 T1=T2; 44 S1=S2; 45 C1=C2; 46 R1=R2; 47 if(k==1) 48 { 49 k++; 50 continue; 51 } 52 C2=(16.0*S2-S1)/15.0; 53 if(k==2) 54 { 55 k++; 56 continue; 57 } 58 R2=(64.0*C2-C1)/63.0; 59 if(k==3) 60 { 61 k++; 62 continue; 63 } 64 if(fabs(R1-R2)<e||counter>=100)break; 65 } 66 return R2; 67 } 68 double Tn(double a,double b,double e) 69 { 70 double T1,T2; 71 double h=b-a; 72 T1=(fx(a)+fx(b))*h/2.0; 73 while(1) 74 { 75 Tk++; 76 double s=getS(a,b,h); 77 T2=(T1+h*s)/2.0; 78 if(fabs(T2-T1)<e)break; 79 h/=2.0; 80 T1=T2; 81 } 82 return T2; 83 } 84 int main() 85 { 86 double a,b,e; 87 printf("输入积分限和精度: a b e:"); 88 //输入区间[a,b],和精度e 89 scanf("%lf%lf%lf",&a,&b,&e); 90 double t=Romberg(a,b,e); 91 //分别输出龙贝格算法和梯形法的计算结果和相应二分次数 92 printf("\nRomberg:积分值:%.7lf -- 二分次数:%d\n",t,Rk); 93 t=Tn(a,b,e); 94 printf(" Tn:积分值:%.7lf -- 二分次数:%d\n",t,Tk); 95 double tf = getReal(a,b); 96 printf(" Real:%.7lf",tf); 97 return 0; 98 }
标签:输入 误差 str can TE lock rom ios size
原文地址:https://www.cnblogs.com/duye/p/9118957.html