标签:官网 样式 范围 close 查看 列表 [1] 使用 邻居
一.networkx
1.用于图论和复杂网络
2.官网:http://networkx.github.io/
3.networkx常常结合numpy等数据处理相关的库一起使用,通过matplot来可视化图
二.绘制图
1.创建图

1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 G=nx.Graph()#创建空图,无向图 5 # G1=nx.DiGraph(e)#创建空图,有向图 6 # G = nx.Graph(name=‘my graph‘)#指定图的属性(name) 的值(my graph) 7 G.add_edges_from(([1,2],[2,3],[3,1])) 8 9 e = [(1, 2), (2, 3), (3, 4)] # 边的列表 10 G2 = nx.Graph(e)#根据e来创建图 11 12 F=G.to_directed()#把无向图转换为有向图 13 14 #创建多图,类MultiGraph和类MultiDiGraph允许添加相同的边两次,这两条边可能附带不同的权值 15 # H=nx.MultiGraph(e) 16 H=nx.MultiDiGraph(e) 17 18 plt.subplot(2,2,1) 19 nx.draw(G,with_labels=True) 20 plt.subplot(2,2,2) 21 nx.draw(G2,with_labels=True) 22 plt.subplot(2,2,3) 23 nx.draw(F,with_labels=True) 24 plt.subplot(2,2,4) 25 nx.draw(H,with_labels=True) 26 27 plt.show()
2.无向图

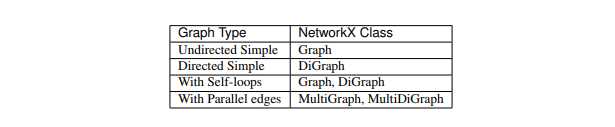
1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 G=nx.Graph()#创建空图 5 6 #添加节点 7 G.add_node(‘a‘) 8 G.add_node(1) #添加单个节点 9 G.add_nodes_from([2,3,4]) #添加一些节点,容器,(可以是list, dict, set,) 10 11 #添加边,如果点不在图中,会自动创建点 12 G.add_edge(1,‘a‘,weight=1.2) #添加单条边,连接1,‘a’的边,可以赋予边属性以及他的值 13 G.add_edges_from([(2,3),(3,4)])#添加一些边(列表) 14 G.add_weighted_edges_from([(1,‘a‘,0.1),(4,2,0.5)])#给边赋予权重 15 16 #移除边 17 G.remove_edge(2,4) #移除一条边 18 G.remove_edges_from([(3,4),]) #移除一些边 19 20 #移除节点,同时移除他对应的边 21 G.remove_node(1) #移除单个节点 22 G.remove_nodes_from([4,]) #移除一些节点 23 24 #绘图 25 nx.draw(G, # 图 26 pos=nx.circular_layout(G), # 图的布局 27 alpha=0.5, # 图的透明度(默认1.0不透明,0完全透明) 28 29 with_labels=True, # 节点是否带标签 30 font_size=18, # 节点标签字体大小 31 node_size=400, # 指定节点的尺寸大小 32 node_color=‘blue‘, # 指定节点的颜色 33 node_shape=‘o‘, # 节点的形状 34 35 edge_color=‘r‘, # 边的颜色 36 width=0.8, # 边的宽度 37 style=‘solid‘, # 边的样式 38 39 ax=None, # Matplotlib Axes对象,可选在指定的Matplotlib轴中绘制图形。 40 ) 41 42 plt.show()

绘图布局
3.有向图和无向图的最大差别在于:有向图中的边是有顺序的,前一个表示开始节点,后一个表示结束节点。
三.图
数据结构


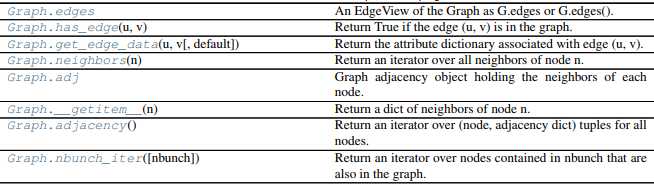
1.图的属性

1 #像color,label,weight或者其他Python对象的属性都可以被设置为graph,node,edge的属性 2 # 每个graph,node,edge都能够包含key/value这样的字典数据 3 import networkx as nx 4 import matplotlib.pyplot as plt 5 6 G=nx.DiGraph([(1,2),(2,3),(3,4),(1,4),(4,2)],name=‘my digraph‘,a=‘b‘) 7 #创建一个有向图,赋予边,点,权重,以及有向图的属性name的值my digraph 8 9 #属性都可以在定义时赋予,或者通过直接赋值来添加修改 10 #图属性 11 print(G)#图的名称 12 print(G.graph)#图的属性,字典 13 G.graph[‘b‘]=19#赋予属性 14 print(G.graph) 15 print(‘#‘*60) 16 17 #节点属性 18 print(‘图的节点:‘,G.nodes)#列表 19 print(‘节点个数:‘,G.number_of_nodes()) 20 G.add_node(‘b‘,time=‘0.2‘) 21 print(G.node[‘b‘])#显示单个节点的信息 22 G.node[‘b‘][‘time‘]=0.3#修改属性 23 print(G.node[‘b‘]) 24 print(‘#‘*60) 25 26 #边属性 27 print(‘图的边:‘,G.edges)#列表 28 print (‘边的个数:‘,G.number_of_edges()) 29 G.add_edge(‘a‘,‘b‘,weight=0.6) 30 G.add_edges_from( [ (2,3),(3,4) ], color="red") 31 G.add_edges_from( [(1,2,{"color":"blue"}),(4,5,{"weight":8})]) 32 G[1][2]["width"]=4.7#添加或修改属性 33 print(G.get_edge_data(1, 2))#获取某条边的属性 34 print(‘#‘*60) 35 36 nx.draw(G,pos = nx.circular_layout(G),with_labels=True) 37 38 plt.show 39 -------------------------------------------------------------------------- 40 my digraph 41 {‘name‘: ‘my digraph‘, ‘a‘: ‘b‘} 42 {‘name‘: ‘my digraph‘, ‘a‘: ‘b‘, ‘b‘: 19} 43 ############################################################ 44 图的节点: [1, 2, 3, 4] 45 节点个数: 4 46 {‘time‘: ‘0.2‘} 47 {‘time‘: 0.3} 48 {2: {}, 4: {}} 49 ############################################################ 50 图的边: [(1, 2), (1, 4), (2, 3), (3, 4), (4, 2)] 51 边的个数: 5 52 {‘color‘: ‘blue‘, ‘width‘: 4.7}
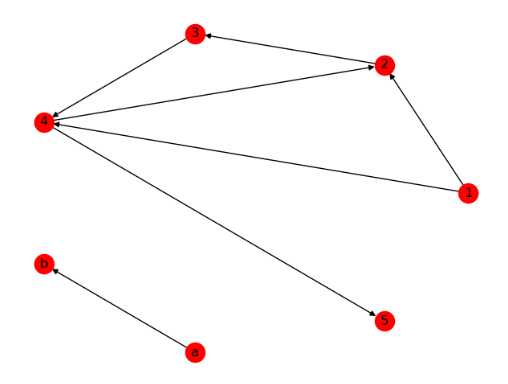
2.边和节点

1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 G=nx.DiGraph([(1,2,{‘weight‘:10}),(2,3),(3,4),(1,4),(4,2)]) 5 6 nx.add_path(G, [0, 4,3])#在图中添加路径 7 8 # 对1节点进行分析 9 print(G.node[1])#节点1的信息 10 G.node[1][‘time‘]=1#赋予节点属性 11 print(G.node[1]) 12 print(G[1]) # 1相关的节点的信息,他的邻居和对应的边的属性 13 print(G.degree(1)) # 1节点的度 14 print(‘#‘*60) 15 16 # 对【1】【2】边进行分析 17 print(G[1][2]) # 查看某条边的属性 18 G[1][2][‘weight‘] = 0.4 # 重新设置边的权重 19 print(G[1][2][‘weight‘]) # 查看边的权重 20 G[1][2][‘color‘] = ‘blue‘ # 添加属性 21 print(G[1][2]) 22 23 nx.draw(G,pos = nx.circular_layout(G),with_labels=True) 24 25 plt.show() 26 ------------------------------------------------------------------ 27 {} 28 {‘time‘: 1} 29 {2: {‘weight‘: 10}, 4: {}} 30 2 31 ############################################################ 32 {‘weight‘: 10} 33 0.4 34 {‘weight‘: 0.4, ‘color‘: ‘blue‘}
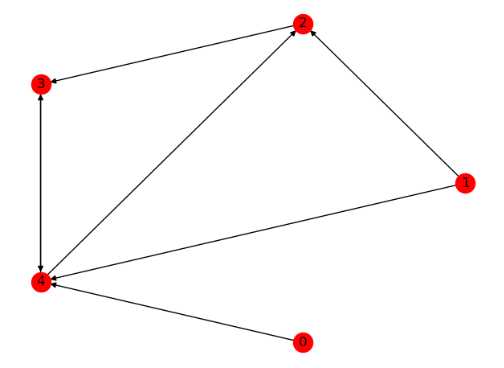
3.有向图

1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 G=nx.DiGraph([(1,2,{‘weight‘:10}),(2,3),(3,4),(1,4),(4,2)]) 5 print(‘#‘*60) 6 print(G.edges)#An OutEdgeView of the DiGraph as G.edges or G.edges(). 7 print(G.out_edges)#An OutEdgeView of the DiGraph as G.edges or G.edges(). 8 print(G.in_edges)#An InEdgeView of the Graph as G.in_edges or G.in_edges() 9 print(‘#‘*60) 10 11 print(G.degree)#图的度 12 print(G.out_degree)#图的出度 13 print(G.in_degree)#图的入度 14 print(‘#‘*60) 15 16 print(G.adj)#Graph adjacency object holding the neighbors of each node 17 print(G.neighbors(2))#节点2的邻居 18 print(G.succ)#Graph adjacency object holding the successors of each node 19 print(G.successors(2))#节点2的后继节点 20 print(G.pred)#Graph adjacency object holding the predecessors of each node 21 print(G.predecessors(2))#节点2的前继节点 22 #以列表形式打印 23 print([n for n in G.neighbors(2)]) 24 print([n for n in G.successors(2)]) 25 print([n for n in G.predecessors(2)]) 26 27 nx.draw(G,pos = nx.circular_layout(G),with_labels=True) 28 29 plt.show() 30 -------------------------------------------------------- 31 ############################################################ 32 [(1, 2), (1, 4), (2, 3), (3, 4), (4, 2)] 33 [(1, 2), (1, 4), (2, 3), (3, 4), (4, 2)] 34 [(1, 2), (4, 2), (2, 3), (3, 4), (1, 4)] 35 ############################################################ 36 [(1, 2), (2, 3), (3, 2), (4, 3)] 37 [(1, 2), (2, 1), (3, 1), (4, 1)] 38 [(1, 0), (2, 2), (3, 1), (4, 2)] 39 ############################################################ 40 {1: {2: {‘weight‘: 10}, 4: {}}, 2: {3: {}}, 3: {4: {}}, 4: {2: {}}} 41 <dict_keyiterator object at 0x0DA2BF00> 42 {1: {2: {‘weight‘: 10}, 4: {}}, 2: {3: {}}, 3: {4: {}}, 4: {2: {}}} 43 <dict_keyiterator object at 0x0DA2BF00> 44 {1: {}, 2: {1: {‘weight‘: 10}, 4: {}}, 3: {2: {}}, 4: {3: {}, 1: {}}} 45 <dict_keyiterator object at 0x0DA2BF00> 46 [3] 47 [3] 48 [1, 4]
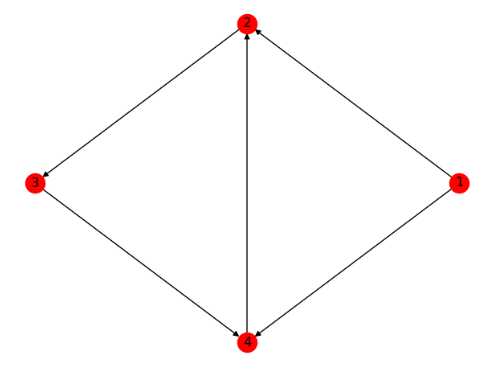
4.图的操作
Applying classic graph operations


1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 G=nx.DiGraph([(1,2,{‘weight‘:10}),(2,1,{‘weight‘:1}),(2,3),(3,4),(1,4),(4,2)]) 5 G2=nx.DiGraph([(1,‘a‘),(‘a‘,‘b‘),(1,4)]) 6 7 H=G.subgraph([1,2,4])#产生关于节点的子图 8 9 G3=nx.compose(H,G2)#结合两个图并表示两者共同的节点 10 11 plt.subplot(221) 12 nx.draw(G,pos = nx.circular_layout(G),with_labels=True,name=‘G‘) 13 14 plt.subplot(222) 15 nx.draw(H,pos = nx.circular_layout(G),with_labels=True) 16 17 plt.subplot(223) 18 nx.draw(G2,with_labels=True) 19 20 plt.subplot(224) 21 nx.draw(G3,with_labels=True) 22 23 plt.show()
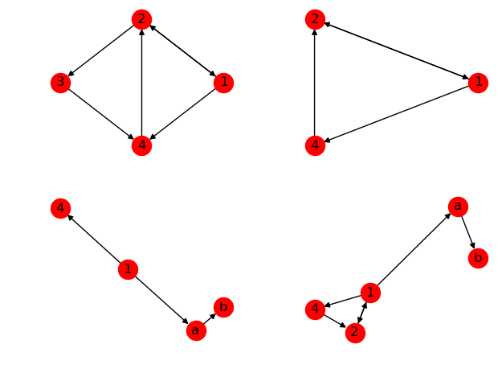
4.算法
...
四.简单根据数据画图

1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 #1.导入数据: 5 # networkx支持的直接处理的数据文件格式adjlist/edgelist/gexf/gml/pickle/graphml/json/lead/yaml/graph6/sparse6/pajek/shp/ 6 #根据实际情况,把文件变为gml文件 7 G1 = nx.DiGraph() 8 with open(‘file.txt‘) as f: 9 for line in f: 10 cell = line.strip().split(‘,‘) 11 G1.add_weighted_edges_from([(cell[0],cell[1],cell[2])]) 12 nx.write_gml(G1,‘file.gml‘)#写网络G进GML文件 13 14 G=nx.read_gml("file.gml") #读取gml文件 15 # parse_gml(lines[,relael]) 从字符串中解析GML图 16 # generate_gml(G) 以gml格式生成一个简单条目的网络G 17 18 print(G.nodes) 19 print(G.edges) 20 21 #2.在figure上先设置坐标 22 plt.title("图G") 23 plt.ylabel("y") 24 plt.xlabel("x") 25 plt.xlim(-1,1) 26 plt.ylim(-1,1) 27 28 #再在坐标轴里面调节图形大小 29 #整个figure按照X与Y轴横竖来平均切分,以0到1之间的数值来表示 30 #axes([x,y,xs,ys]),如果不设置 31 #其中x代表在X轴的位置,y代表在Y轴的位置,xs代表在X轴上向右延展的范围大小,yx代表在Y轴中向上延展的范围大小 32 plt.axes([0.1, 0.1, 0.8, 0.8]) 33 34 #3.在axes中绘图 35 nx.draw(G,pos = nx.circular_layout(G),with_labels=True,) 36 37 #4.保存图形 38 plt.savefig("file.png")#将图像保存到一个文件 39 40 plt.show() 41 ----------------------------------------------------- 42 [‘6‘, ‘2‘, ‘5‘, ‘1‘, ‘15‘, ‘4‘, ‘3‘, ‘13‘, ‘16‘, ‘10‘, ‘7‘, ‘21‘, ‘20‘, ‘8‘, ‘17‘, ‘23‘, ‘25‘, ‘26‘, ‘28‘, ‘29‘, ‘31‘, ‘32‘, ‘34‘, ‘35‘, ‘36‘, ‘37‘, ‘44‘, ‘39‘, ‘45‘, ‘19‘, ‘46‘, ‘47‘, ‘51‘, ‘52‘, ‘53‘, ‘54‘, ‘41‘, ‘55‘, ‘57‘, ‘61‘, ‘65‘, ‘56‘, ‘66‘, ‘69‘, ‘70‘, ‘71‘, ‘72‘, ‘74‘, ‘75‘, ‘68‘, ‘64‘, ‘76‘, ‘77‘, ‘78‘, ‘60‘, ‘79‘, ‘80‘, ‘81‘, ‘62‘, ‘83‘, ‘104‘, ‘86‘, ‘87‘, ‘89‘, ‘94‘, ‘95‘, ‘96‘, ‘97‘, ‘99‘, ‘88‘, ‘101‘, ‘100‘, ‘103‘, ‘105‘, ‘106‘, ‘107‘, ‘108‘, ‘109‘, ‘110‘, ‘111‘, ‘112‘, ‘115‘, ‘114‘, ‘119‘, ‘122‘, ‘127‘, ‘129‘, ‘116‘, ‘131‘, ‘132‘, ‘133‘, ‘113‘, ‘125‘, ‘135‘] 43 [(‘6‘, ‘2‘), (‘6‘, ‘5‘), (‘6‘, ‘4‘), (‘6‘, ‘7‘), (‘6‘, ‘114‘), (‘6‘, ‘32‘), (‘2‘, ‘21‘), (‘2‘, ‘20‘), (‘2‘, ‘4‘), (‘2‘, ‘54‘), (‘2‘, ‘132‘), (‘5‘, ‘1‘), (‘5‘, ‘6‘), (‘5‘, ‘7‘), (‘1‘, ‘15‘), (‘1‘, ‘5‘), (‘1‘, ‘32‘), (‘1‘, ‘34‘), (‘1‘, ‘17‘), (‘1‘, ‘31‘), (‘1‘, ‘13‘), (‘1‘, ‘20‘), (‘1‘, ‘54‘), (‘1‘, ‘56‘), (‘1‘, ‘71‘), (‘1‘, ‘74‘), (‘1‘, ‘78‘), (‘1‘, ‘68‘), (‘1‘, ‘81‘), (‘1‘, ‘101‘), (‘1‘, ‘119‘), (‘1‘, ‘2‘), (‘1‘, ‘76‘), (‘1‘, ‘23‘), (‘15‘, ‘97‘), (‘15‘, ‘70‘), (‘4‘, ‘3‘), (‘4‘, ‘26‘), (‘4‘, ‘6‘), (‘4‘, ‘31‘), (‘4‘, ‘57‘), (‘4‘, ‘61‘), (‘4‘, ‘66‘), (‘4‘, ‘72‘), (‘4‘, ‘41‘), (‘4‘, ‘87‘), (‘4‘, ‘39‘), (‘13‘, ‘16‘), (‘13‘, ‘10‘), (‘13‘, ‘17‘), (‘13‘, ‘29‘), (‘13‘, ‘1‘), (‘13‘, ‘34‘), (‘13‘, ‘7‘), (‘13‘, ‘54‘), (‘10‘, ‘1‘), (‘10‘, ‘6‘), (‘10‘, ‘21‘), (‘10‘, ‘8‘), (‘10‘, ‘25‘), (‘10‘, ‘2‘), (‘10‘, ‘3‘), (‘7‘, ‘5‘), (‘7‘, ‘34‘), (‘7‘, ‘6‘), (‘7‘, ‘29‘), (‘7‘, ‘13‘), (‘7‘, ‘3‘), (‘7‘, ‘36‘), (‘7‘, ‘53‘), (‘7‘, ‘55‘), (‘7‘, ‘20‘), (‘7‘, ‘28‘), (‘7‘, ‘76‘), (‘7‘, ‘19‘), (‘7‘, ‘89‘), (‘7‘, ‘109‘), (‘7‘, ‘111‘), (‘7‘, ‘100‘), (‘7‘, ‘47‘), (‘7‘, ‘122‘), (‘7‘, ‘116‘), (‘7‘, ‘133‘), (‘7‘, ‘54‘), (‘21‘, ‘2‘), (‘21‘, ‘1‘), (‘21‘, ‘10‘), (‘21‘, ‘8‘), (‘21‘, ‘3‘), (‘21‘, ‘36‘), (‘21‘, ‘39‘), (‘21‘, ‘7‘), (‘8‘, ‘1‘), (‘17‘, ‘3‘), (‘17‘, ‘23‘), (‘17‘, ‘28‘), (‘17‘, ‘13‘), (‘17‘, ‘20‘), (‘17‘, ‘1‘), (‘17‘, ‘81‘), (‘17‘, ‘39‘), (‘23‘, ‘17‘), (‘23‘, ‘19‘), (‘23‘, ‘32‘), (‘23‘, ‘20‘), (‘23‘, ‘69‘), (‘23‘, ‘7‘), (‘23‘, ‘108‘), (‘26‘, ‘4‘), (‘28‘, ‘7‘), (‘28‘, ‘69‘), (‘28‘, ‘132‘), (‘29‘, ‘13‘), (‘29‘, ‘51‘), (‘29‘, ‘52‘), (‘29‘, ‘7‘), (‘31‘, ‘4‘), (‘31‘, ‘1‘), (‘32‘, ‘6‘), (‘32‘, ‘1‘), (‘32‘, ‘23‘), (‘34‘, ‘7‘), (‘34‘, ‘1‘), (‘34‘, ‘13‘), (‘35‘, ‘6‘), (‘35‘, ‘1‘), (‘35‘, ‘65‘), (‘35‘, ‘69‘), (‘35‘, ‘70‘), (‘35‘, ‘79‘), (‘36‘, ‘37‘), (‘36‘, ‘46‘), (‘36‘, ‘41‘), (‘36‘, ‘21‘), (‘36‘, ‘7‘), (‘36‘, ‘78‘), (‘37‘, ‘36‘), (‘37‘, ‘44‘), (‘44‘, ‘37‘), (‘44‘, ‘39‘), (‘39‘, ‘45‘), (‘39‘, ‘7‘), (‘39‘, ‘44‘), (‘39‘, ‘21‘), (‘39‘, ‘69‘), (‘39‘, ‘17‘), (‘39‘, ‘4‘), (‘39‘, ‘109‘), (‘39‘, ‘114‘), (‘45‘, ‘39‘), (‘45‘, ‘53‘), (‘45‘, ‘54‘), (‘46‘, ‘36‘), (‘47‘, ‘1‘), (‘47‘, ‘7‘), (‘51‘, ‘29‘), (‘52‘, ‘29‘), (‘53‘, ‘45‘), (‘53‘, ‘7‘), (‘54‘, ‘45‘), (‘54‘, ‘1‘), (‘54‘, ‘62‘), (‘54‘, ‘129‘), (‘54‘, ‘13‘), (‘54‘, ‘2‘), (‘54‘, ‘7‘), (‘41‘, ‘36‘), (‘41‘, ‘75‘), (‘41‘, ‘60‘), (‘41‘, ‘4‘), (‘41‘, ‘83‘), (‘41‘, ‘104‘), (‘41‘, ‘86‘), (‘41‘, ‘89‘), (‘41‘, ‘70‘), (‘41‘, ‘105‘), (‘41‘, ‘110‘), (‘41‘, ‘68‘), (‘41‘, ‘64‘), (‘55‘, ‘7‘), (‘57‘, ‘4‘), (‘57‘, ‘110‘), (‘61‘, ‘4‘), (‘61‘, ‘20‘), (‘61‘, ‘2‘), (‘61‘, ‘77‘), (‘65‘, ‘35‘), (‘56‘, ‘1‘), (‘66‘, ‘4‘), (‘69‘, ‘39‘), (‘69‘, ‘35‘), (‘69‘, ‘23‘), (‘69‘, ‘28‘), (‘69‘, ‘62‘), (‘69‘, ‘81‘), (‘69‘, ‘99‘), (‘70‘, ‘95‘), (‘70‘, ‘41‘), (‘70‘, ‘35‘), (‘70‘, ‘96‘), (‘70‘, ‘15‘), (‘71‘, ‘1‘), (‘72‘, ‘4‘), (‘74‘, ‘1‘), (‘68‘, ‘64‘), (‘68‘, ‘1‘), (‘68‘, ‘97‘), (‘68‘, ‘41‘), (‘64‘, ‘68‘), (‘64‘, ‘80‘), (‘64‘, ‘94‘), (‘64‘, ‘112‘), (‘64‘, ‘41‘), (‘76‘, ‘7‘), (‘76‘, ‘1‘), (‘77‘, ‘39‘), (‘77‘, ‘15‘), (‘77‘, ‘6‘), (‘77‘, ‘1‘), (‘77‘, ‘23‘), (‘77‘, ‘28‘), (‘77‘, ‘115‘), (‘77‘, ‘112‘), (‘77‘, ‘131‘), (‘77‘, ‘61‘), (‘78‘, ‘1‘), (‘78‘, ‘60‘), (‘78‘, ‘36‘), (‘60‘, ‘41‘), (‘60‘, ‘78‘), (‘60‘, ‘87‘), (‘60‘, ‘108‘), (‘60‘, ‘112‘), (‘60‘, ‘56‘), (‘79‘, ‘35‘), (‘80‘, ‘25‘), (‘81‘, ‘17‘), (‘81‘, ‘69‘), (‘81‘, ‘1‘), (‘81‘, ‘107‘), (‘62‘, ‘69‘), (‘62‘, ‘54‘), (‘83‘, ‘41‘), (‘104‘, ‘41‘), (‘104‘, ‘108‘), (‘86‘, ‘41‘), (‘87‘, ‘4‘), (‘87‘, ‘60‘), (‘89‘, ‘41‘), (‘89‘, ‘7‘), (‘94‘, ‘64‘), (‘95‘, ‘70‘), (‘96‘, ‘70‘), (‘96‘, ‘106‘), (‘96‘, ‘107‘), (‘96‘, ‘15‘), (‘97‘, ‘15‘), (‘97‘, ‘68‘), (‘99‘, ‘69‘), (‘88‘, ‘7‘), (‘101‘, ‘1‘), (‘101‘, ‘103‘), (‘100‘, ‘101‘), (‘100‘, ‘60‘), (‘100‘, ‘1‘), (‘100‘, ‘7‘), (‘105‘, ‘41‘), (‘106‘, ‘96‘), (‘107‘, ‘81‘), (‘107‘, ‘96‘), (‘108‘, ‘60‘), (‘108‘, ‘23‘), (‘108‘, ‘104‘), (‘109‘, ‘7‘), (‘109‘, ‘39‘), (‘110‘, ‘57‘), (‘110‘, ‘41‘), (‘111‘, ‘7‘), (‘112‘, ‘64‘), (‘112‘, ‘77‘), (‘112‘, ‘115‘), (‘112‘, ‘60‘), (‘115‘, ‘77‘), (‘114‘, ‘39‘), (‘119‘, ‘1‘), (‘119‘, ‘127‘), (‘119‘, ‘25‘), (‘122‘, ‘7‘), (‘127‘, ‘119‘), (‘127‘, ‘132‘), (‘129‘, ‘54‘), (‘116‘, ‘7‘), (‘132‘, ‘127‘), (‘132‘, ‘2‘), (‘132‘, ‘28‘), (‘133‘, ‘7‘), (‘113‘, ‘125‘), (‘113‘, ‘23‘), (‘113‘, ‘135‘), (‘125‘, ‘113‘), (‘135‘, ‘113‘)]
5.分析图

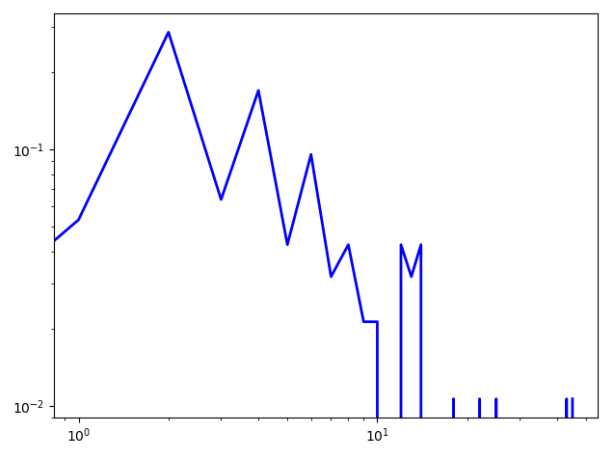
1 import networkx as nx 2 import matplotlib.pyplot as plt 3 4 G=nx.read_gml("file.gml") 5 UG=G.to_undirected() 6 7 #网络信息 8 print(nx.info(G)) 9 eccen = nx.eccentricity(UG)#节点离心度 10 print(eccen) 11 print(max(eccen.values())) 12 print(min(eccen.values())) 13 # print(nx.diameter(G)) # 网络直径 14 # print(nx.radius(G)) #网络半径 15 print(nx.average_shortest_path_length(G)) # 网络平均最短距离 16 print(nx.average_shortest_path_length(UG)) # 网络平均最短距离 17 18 #度分布 19 degree=nx.degree_histogram(G)#所有节点的度分布序列 20 print(degree) 21 x=range(len(degree)) #生成x轴序列 22 y=[z/float(sum(degree))for z in degree]#将频次转换为频率 23 plt.loglog(x,y,color=‘blue‘,linewidth=2)#在双对数坐标轴上绘制分布曲线 24 25 #度中心度 26 print(nx.degree_centrality(G))#计算每个点的度中心性 27 print(nx.in_degree_centrality(G))#计算每个点的入度中心性 28 print(nx.out_degree_centrality(G))#计算每个点的出度中心性 29 30 #紧密中心度 31 print(nx.closeness_centrality(G)) 32 33 #介数中心度 34 print(nx.betweenness_centrality(G)) 35 36 #特征向量中心度 37 print(nx.eigenvector_centrality(G)) 38 39 #网络密度 40 print(nx.density(G)) 41 42 #网络传递性 43 print(nx.transitivity(G)) 44 45 #网络群聚系数 46 print(nx.average_clustering(UG)) 47 print(nx.clustering(UG)) 48 49 #节点度的匹配性 50 print(nx.degree_assortativity_coefficient(UG)) 51 52 plt.show() 53 ------------------------------------------------------------------
标签:官网 样式 范围 close 查看 列表 [1] 使用 邻居
原文地址:https://www.cnblogs.com/yu-liang/p/9117643.html