归并排序之python

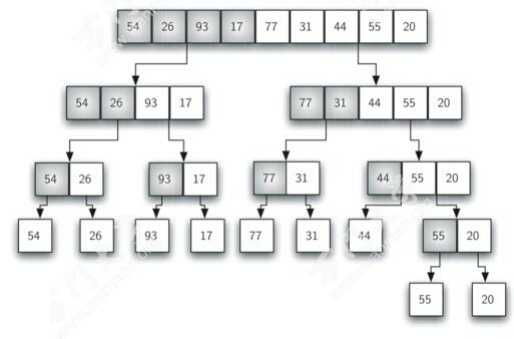
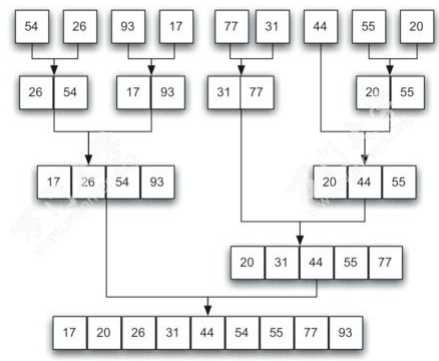
#算法时间复杂度 O(logN)
#递归
#两个步骤：1.拆分 2.合并

def _merge(a: list, b: list) -> list:
    #合并两个排序表
    c = []
    while len(a) > 0 and len(b) > 0:
        if a[0] < b[0]:
            c.append(a[0])
            a.remove(a[0])
        else:
            c.append(b[0])
            b.remove(b[0])

    if len(a) == 0:
        c += b
    else:
        c += a
    return c


def _merge_sorted(nums: list) -> list:
    # Won‘t sort in place
    if len(nums) <= 1:
        return nums

    m = len(nums) // 2
    a = _merge_sorted(nums[:m])     #前半
    b = _merge_sorted(nums[m:])　　　#后半
    return _merge(a, b)


# Wrapper包装器
def merge_sorted(nums: list, reverse=False) -> list:
    import time
    start = time.time()
    #归并排序
    nums = _merge_sorted(nums)
    if reverse:
        nums = nums[::-1]

    t = time.time() - start
    return nums, len(nums), t

lis = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
merge_sorted(l, reverse=False)[0]

#输出结果
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]