标签:构造 最小 单选 直接 src 插入 完全 技术 完全二叉树
堆是具有下列性质的完全二叉树:
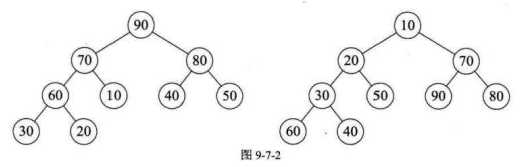
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆 (例如图 9-2 左图所示) ;
或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(例如图 9-2 右图所示)。
前面介绍的(简单)选择排序,需要每次从未排序序列中选出最小(最大)的数据。我们当时的实现是每次都将未排序序列从头开始比较,其实从第二次开始就出现了大量的重复比较,即没有充分利用前一次的比较结果。
如果可以做到每次在选择到最小记录的同时,并根据比较结果对其他数据做出相应的调整 , 那样排序的总体效率就会非常高了 。所以用堆结构进行实现。
堆排序 (Heap Sort) 就是利用堆(假设利用大顶堆)进行排序的方法。
它的基本思想是, 将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值) .然后将剩余的 n - 1 个序列重新构造成一个堆,这样就得到 n 个元素中的次小值。如此反复执行, 便能得到一个有序序列了 。
实现
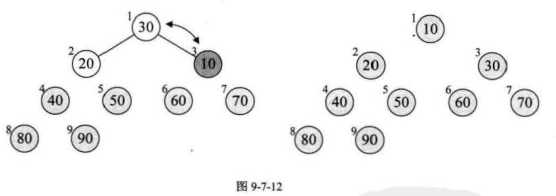
1 public static void heapSort(int[] array) { 2 buildHeap(array); 3 int len = array.length; 4 int i = 0; 5 for (i = len - 1; i >= 1; i--) { 6 swap(array, 0, i); // 将堆顶元素与堆的最后一个元素互换;并从堆中去掉最后一个元素(即i每次减1) 7 heapify(array, 0, i); // 从新的堆顶元素开始向下进行堆调整,时间复杂度O(logn) 8 } 9 } 10 11 // 构建堆 12 /* 13 * 这是第一个for循环 14 * 假设需要排序的序列有9个元素(数组中位置0-8),我们首先要找到每个非终端结点(非叶结点)当作根结点(图9-7-5注意该图位置标注是1-9对应我们的0-8),即第1-4个(位置0-3) 15 * 然后循环就是依次将那4个根节点及其子树调整为大顶堆 16 */ 17 public static void buildHeap(int[] array) { 18 for (int i = array.length / 2 - 1; i >= 0; i--) { 19 heapify(array, i, array.length); 20 } 21 } 22 23 // 调整堆 24 /** 25 * @param data 堆(无序区) 26 * @param parentNode 根节点(子树的) 27 * @param heapSize 堆的结点个数 28 */ 29 public static void heapify(int[] data, int parentNode, int heapSize) { 30 int leftChild = 2 * parentNode + 1;// 左孩子下标 (看图9-7-5注意该图位置标注是1-9对应我们的0-8) 31 int rightChild = 2 * parentNode + 2;// 右孩子下标(如果存在的话) 32 int largest = parentNode; // 选出当前结点与其左右孩子三者之中的最大值 33 // 寻找3个节点中最大值节点的下标 34 if (leftChild < heapSize && data[leftChild] > data[parentNode]) { 35 largest = leftChild; 36 } 37 if (rightChild < heapSize && data[rightChild] > data[largest]) { 38 largest = rightChild; 39 } 40 // 如果最大值不是父节点,那么交换,并继续调整堆 41 if (largest != parentNode) { 42 swap(data, largest, parentNode); // 把当前根结点和它的最大(直接)子节点进行交换 43 heapify(data, largest, heapSize); // 递归调用,继续从当前结点向下进行堆调整 44 } 45 } 46 47 // 交换函数 48 public static void swap(int[] array, int i, int j) { 49 int temp = 0; 50 temp = array[i]; 51 array[i] = array[j]; 52 array[j] = temp; 53 }
图示:
1)输入数组
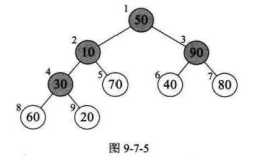
2)构建堆,得到堆(无序区)
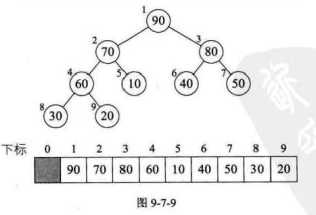
我们程序中数组是按从0下标开始的(即0-8),该图从1下标开始的。
3)开始排序,
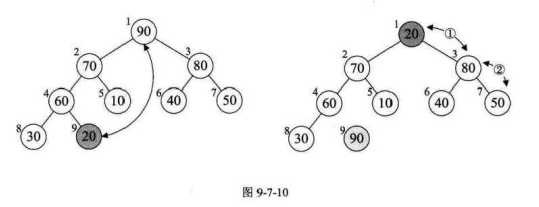
4)最终完成(直到堆的大小由n个元素降到2个)
时间复杂度:
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为 O(n).
在正式排序时,第 i 次取堆顶记录重建堆需要用 O(logi)的时间(完全二叉树的某个结点到根结点的距离为 [Iog2i ] + 1 ,并且需要取 n-1 次堆顶记录,因此,重建堆的时间复杂度为 O(nlogn) 。
所以总体来说,堆排序的时间复杂度为 O(nlogn) 。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为 o(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、 直接插入的 O(n2)的时间复杂度了。
空间复杂度:
只需要一个用了交换的暂存空间,所以空间复杂度为O(1)
稳定性:不稳定
参考:
大话数据结构》
http://www.cnblogs.com/eniac12/p/5329396.html
标签:构造 最小 单选 直接 src 插入 完全 技术 完全二叉树
原文地址:https://www.cnblogs.com/xdyixia/p/9143778.html