R语言数值积分

标签：数位   计算公式   function   length   sap   inf   mat   bsp   png   

　　前两天对学习了R里面计算的基本范围，以及一些求解方程的方法，今天来看看积分，其实上个学期学了数值分析，对这部分的算法是有所了解的，当时是用matlab写了一遍，已经忘了怎么实现的了，现在用R重新写一遍吧，算法有梯形积分法，辛普森积分法，自适应积分法。

• 梯形积分法

　　　　梯形积分法可以用下图很好的解释

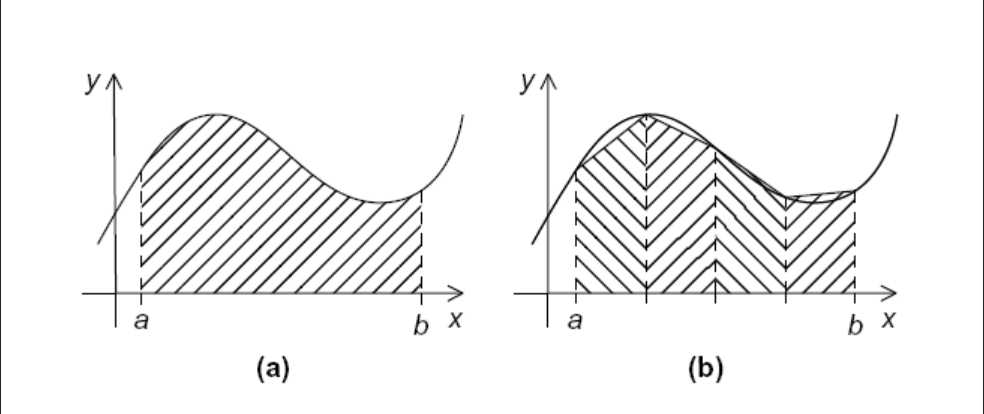　　　　就是将微积分的时候用的方法，取Δx,则一小块面积就约等于f(x)*Δx，连续函数在Δx趋于0的时候，该公式会越来越精确。

###设置小数位数
options(digits = 8)
func1 <- function(x) return(4*x^3)
###梯形积分法
tixing <- function(func, a, b, n=100){
  x <- 0
  h <- (b-a)/n
  for(i in 1:n){
    x <- h*func(a+i*h) + x
  }
  return(x)
}
tixing(func1,0,1,n=10000)

###可以看到这种近似较为粗糙，可以稍微改进一些
tixing2 <- function(func, a, b, n=100){
  h <- (b-a)/n
  add_by <- seq(a,b,by=h)
  f_x <- sapply(add_by,func)
  x <- h*sum(f_x[1]/2,f_x[2:n],f_x[n+1]/2)
  return(x)
}
tixing2(func1,0,1,n=100)

• 辛普森方法

　　　　辛普森方法和梯形方法类似，但是做了改进，前面我们改进的方法用的是梯形逼近，这样子f(x)其实是表示成了一段直线，辛普森方法使用抛物线来拟合，可　　　　　　        以降低误差。

　　　　这里直接给出辛普森的计算公式

　　　　S=h/3(f(x0)+4f(x1)+2f(x2)+4f(x3)+```+4f(xn-1)+f(xn))

###辛普森方法
simpson <- function(func, a, b, n=100){
  h <- (b-a)/n
  
  ###奇数项
  add_by_1 <- seq(a+h,b-h,by=2*h)
  ###偶数项
  add_by_2 <- add_by_1+h
  add_by_2 <- add_by_2[-length(add_by_2)]
  x <- h/3*sum(func(a),4*sapply(add_by_1,func),2*sapply(add_by_2,func),func(b))
  return(x)
}

　　　　目前为止我们指定了运算次数n，而不是指定误差来计算，当然指定误差也是可以的，考虑一种循环，每次n都增加1，就可以完成这个目标了，但是这样运算　　　　        量会越来越大，所以推荐使用另一种方法，即公式本身具有的误差，可以又其本身和其n阶导数一起表示出来，具体的见数值分析相关书籍。

• 自适应积分法

　　　　这种方法我以前也没有过接触，书上讲它的基本思想是越是陡峭（导数大）的函数，需要的分割越细，越是平坦（导数小）的函数，需要的分割越少。详细            的，在进行运算的时候，先限定一个误差，然后将函数分割为两半，每边的误差均是误差的一半。这种方法的程序我再思考一下，还没想到怎么实现较好。

R语言数值积分

标签：数位   计算公式   function   length   sap   inf   mat   bsp   png   

原文地址：https://www.cnblogs.com/NEFPHYS/p/nef20180607.html