标签:tom 识别 总结 方法 bre continue TE 知识 处理
基于贝叶斯的深度神经网络自适应及其在鲁棒自动语音识别中的应用
直接贝叶斯DNN自适应
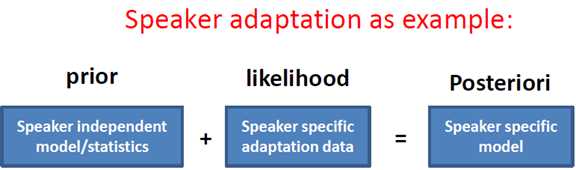
使用高斯先验对DNN进行MAP自适应
为何贝叶斯在模型自适应中很有用?
在实现通用智能时,神经网络需要学习并记住多个任务,任务顺序无标注,任务会不可预期地切换,同种任务可能在很长一段时间内不会复现。当对当前任务B进行学习时,对先前任务A的知识会突然地丢失,这种现象被称为灾难性遗忘(catastrophic forgetting)。
DNN的MAP自适应:理论背景
基于GMM系统的MAP自适应
GMM作为生成性pdf:符合直觉
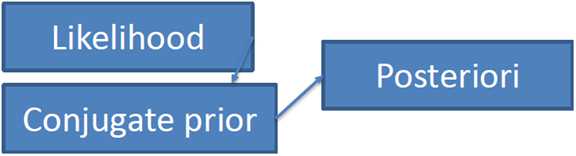
共轭先验(Conjugate Prior)
在贝叶斯统计中,如果后验分布与先验分布属于同类,则先验分布与后验分布被称为共轭分布,而先验分布被称为似然函数的共轭先验。
具体地说,就是给定贝叶斯公式
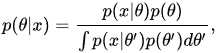
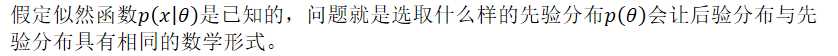
基于DNN的MAP自适应
但是DNN是鉴别性模型,它没有生成性后验概率的概率密度函数。
使得DNN近似为概率密度函数
将DNN的目标函数以概率(似然)形式表示:
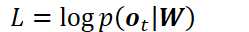
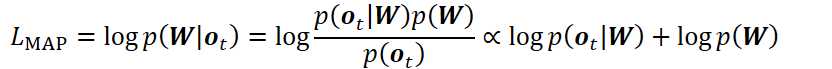
其中似然L可以是交叉熵、最小互信息、最小音素错误、最小分类错误等。
先验估计:经验贝叶斯
对训练说话人进行自适应,并分析说话人直接的参数分布。
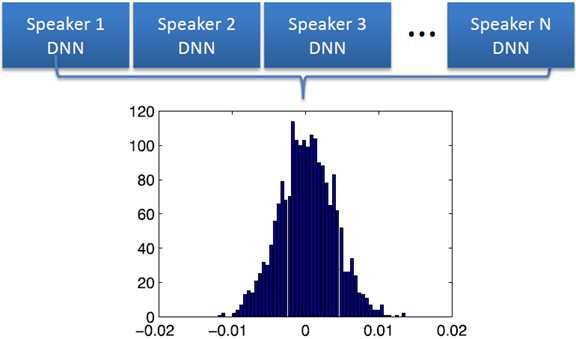
Prior Estimation Cont‘d(先验估计,接上页)
con‘d, Abbreviation of continued, 接上页
假设先验分布为多元高斯
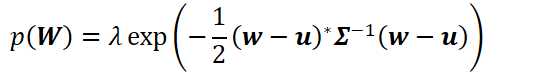
等式右边,只用矢量w完成了对矩阵W的表示(向量化)。
假设先验分布为矩阵高斯
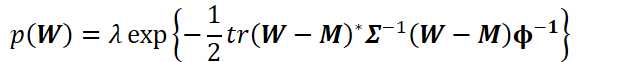
多元高斯与矩阵高斯的结果类似,不过多元高斯先验使用了向量化,更易于处理、更易于简化至到L2正则项。
高斯先验:易于简化至到L2正则项
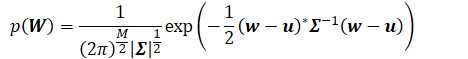
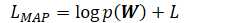
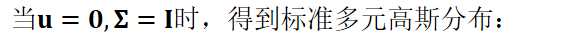
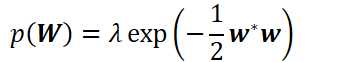
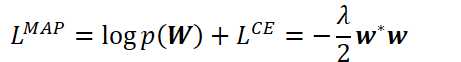
DNN自适应中的灾难性遗忘
自适应后,DNN对自适应数据中见过的类有偏差;
丧失对未观察到样本的识别能力
贝叶斯用于解决灾难性遗忘问题
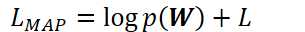
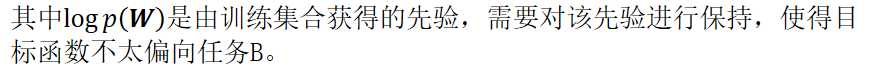
控制参数数量(LHN)
只对插入到线性隐层的仿射变换权重进行适应:冻结其他参数
通常使用一个瓶颈层以控制LHN的大小,进一步较少参数数量。
MAP:只更新激活函数参数
适应隐层中Sigmoid激活函数(AF)参数
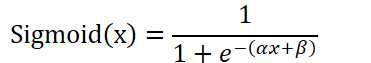
此方法更新的参数比LHN更少。
实验(SWBD)
在此基础之上,以最大后验概率准则更新AF参数,WER进一步降低2.8%(14.4->14.0)
在此基础之上,以最大后验概率准则更新AF参数,WER进一步降低5.0%(13.9->13.2)
间接贝叶斯DNN自适应
对从DNN获得瓶颈特征进行MAP/SMAP
基于DNN瓶颈特征处理后的特征进行MAP/SMAP
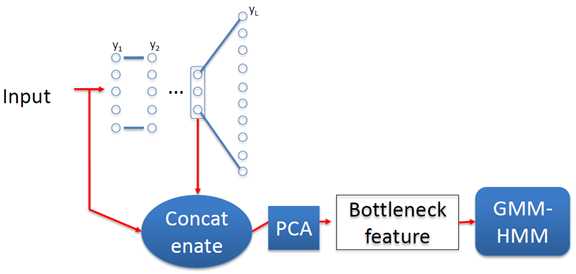
瓶颈特征是鉴别性数据驱动方式训练的;
通过拼接以使用DNN的优点;
要获得瓶颈特征:
MAP/SMAP自适应
MAP
是有效的模型自适应方法,对小数据集鲁棒;
数据量很大时,将蜕化至(相当于)最大似然估计(MLE);
会由于缺少数据,不能更新未见的三音素;
SMAP(Structured MAP)
针对少数据量的结构化MAP自适应
MAP/SMAP实验
瓶颈特征的GMM-HMM略微差与原DNN-HMM(基线)结果(WER提高0.2%,8.84->8.86)
对瓶颈特征进行MAP的GMM-HMM WER降低5.2%(8.84->8.38)
对瓶颈特征进行SMAP的GMM-HMM WER降低11.1%(8.84->7.85)
与MAP-LHN、LHN相比,SMAP最优。
总结
直接DNN自适应:
自适应时,需要对DNN构建一个框架。使用已提出的框架,可以将DNN应用到不同种类型的模型与不同的任务中。
通过瓶颈特征,将DNN"转换"为生成性模型
为DNN提供了使用传统统计学机器学习方法(包括贝叶斯方法)
标签:tom 识别 总结 方法 bre continue TE 知识 处理
原文地址:https://www.cnblogs.com/JarvanWang/p/9152641.html