标签:pen 虚线 ota view 双向 包含 最短路径 原理 int
准备知识:树剖&Splay
先看一道例题:
让你维护一棵给定的树,需要支持下面两种操作:
Change x val: 令x点的点权变为val
Query x y: 计算x,y之间的唯一的最短路径的点权的xor和
这是一道树剖裸题。我们知道,当题目中出现了维护与树上最短路相关的区间操作时,基本可以确定要用树剖来做了。
再来看一下这道题的升级版:
让你维护一棵给定的树,需要支持下面四种操作:
Change x val: 令x点的点权变为val
Query x y: 计算x,y之间的唯一的最短路径的点权xor和
Cut x y: 如果x,y间有边相连,则删除它。
Link x y: 如果x,y不联通,则建立一条x,y之间的有向边。
在这道题里,我们增加了两个操作,Link和Cut。我们发现,这道题不可以用树剖来做了——显然,树剖无法处理修改树的形状的相关操作的。
现在我们就需要LCT了。
LCT,全称Link Cut Tree,中文名“动态树”。顾名思义,这种数据结构就是支持连边和断边操作同时像树剖那样维护一些数据的树。由于需要支持连边断边,LCT就不能像树链剖分一样用线段树来维护了,而需要使用更加灵活的延展树(Splay)。
因此,与树链剖分一样,LCT需要满足以下这些性质:
1.每一个Splay维护的是一条从上到下按在原树中深度严格递增的路径,且中序遍历Splay得到的每个点的深度序列严格递增。
//只要把树剖和Splay搞懂了,这一点不难理解。
2.每一个节点存在且只存在于一个Splay中
3.边分为实边和虚边。实边包含在Splay树中中序遍历的相邻节点之间,而虚边必须由一棵Splay指向另一个节点,也就是中序遍历中最靠前的哪个节点的父亲。
//这里需要注意的是,一般LCT的虚边是用Splay的根节点的father指针来实现的。
辅助理解
当一棵树的虚实边是这样分配的时候,它所对应的伸展树是这个样子:

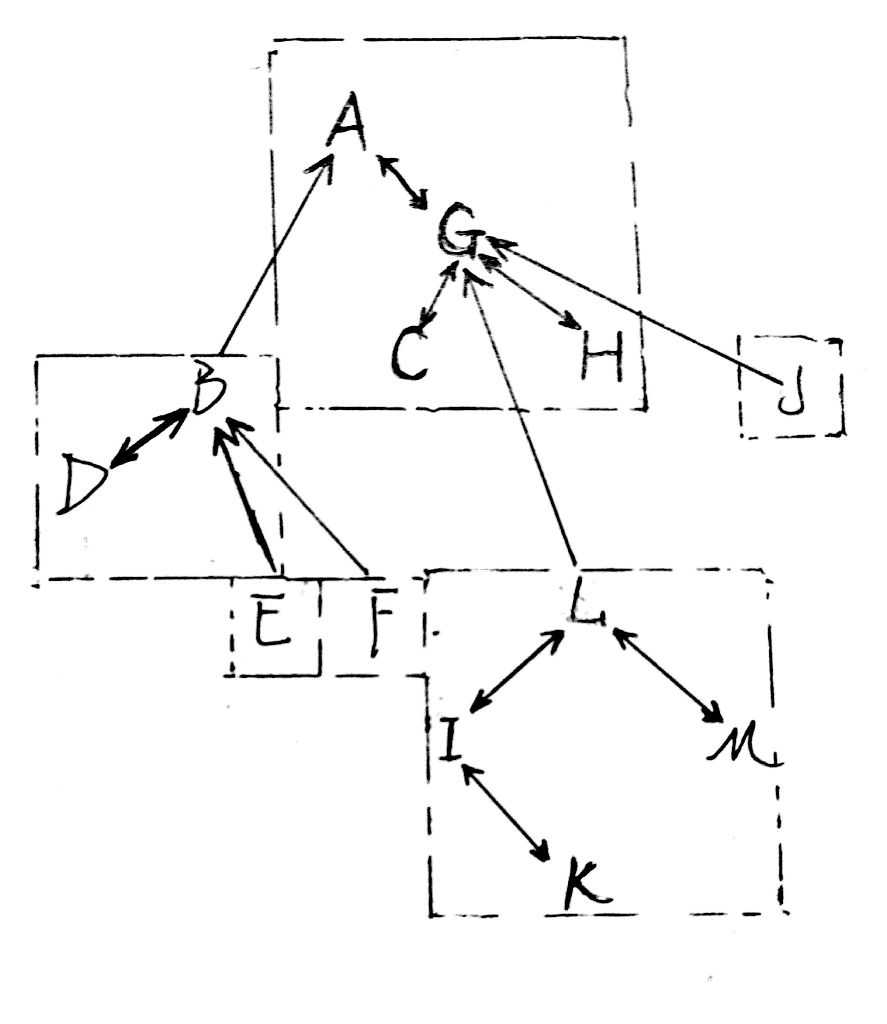
其中,每一个虚线框起来的区域都是一棵伸展树;双向箭头指父节点存son,子节点存father的边;单项箭头指子节点存father,而父节点不存son的边(虚边)。
这个没图的话实在难理解。仍然举一个例子:
如果我们在上图的情况下对节点M执行这一操作,那么这棵树就会有下图的变化:
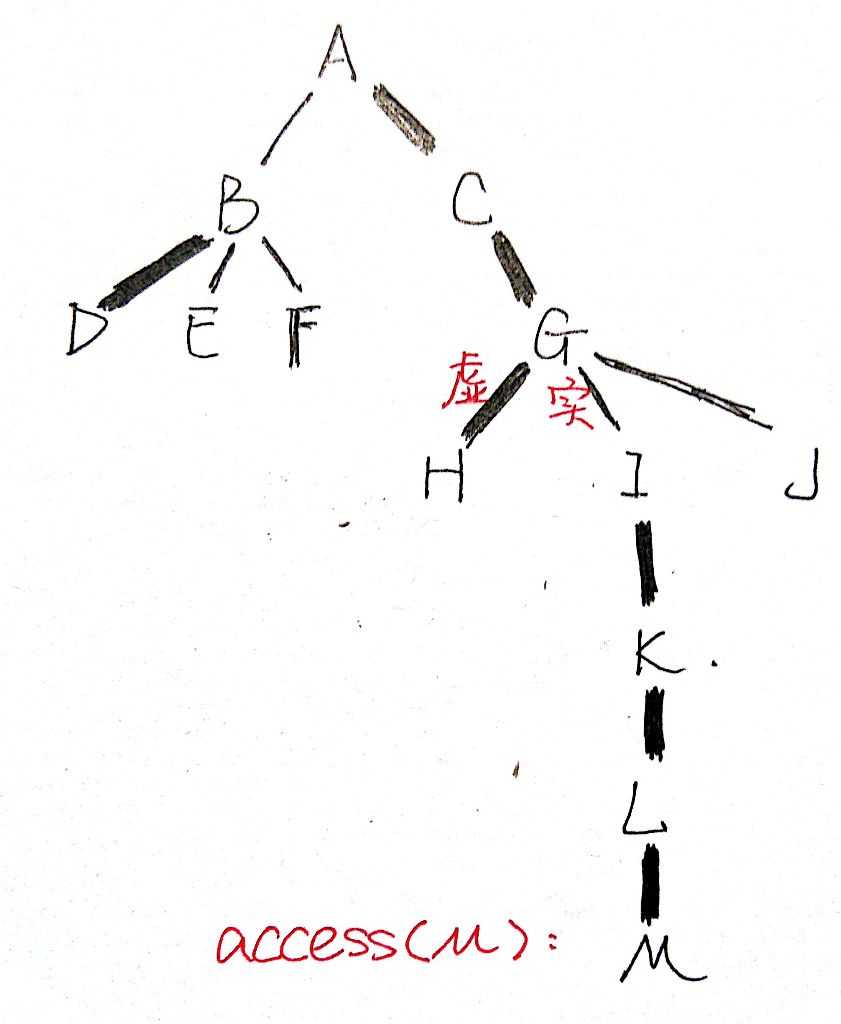
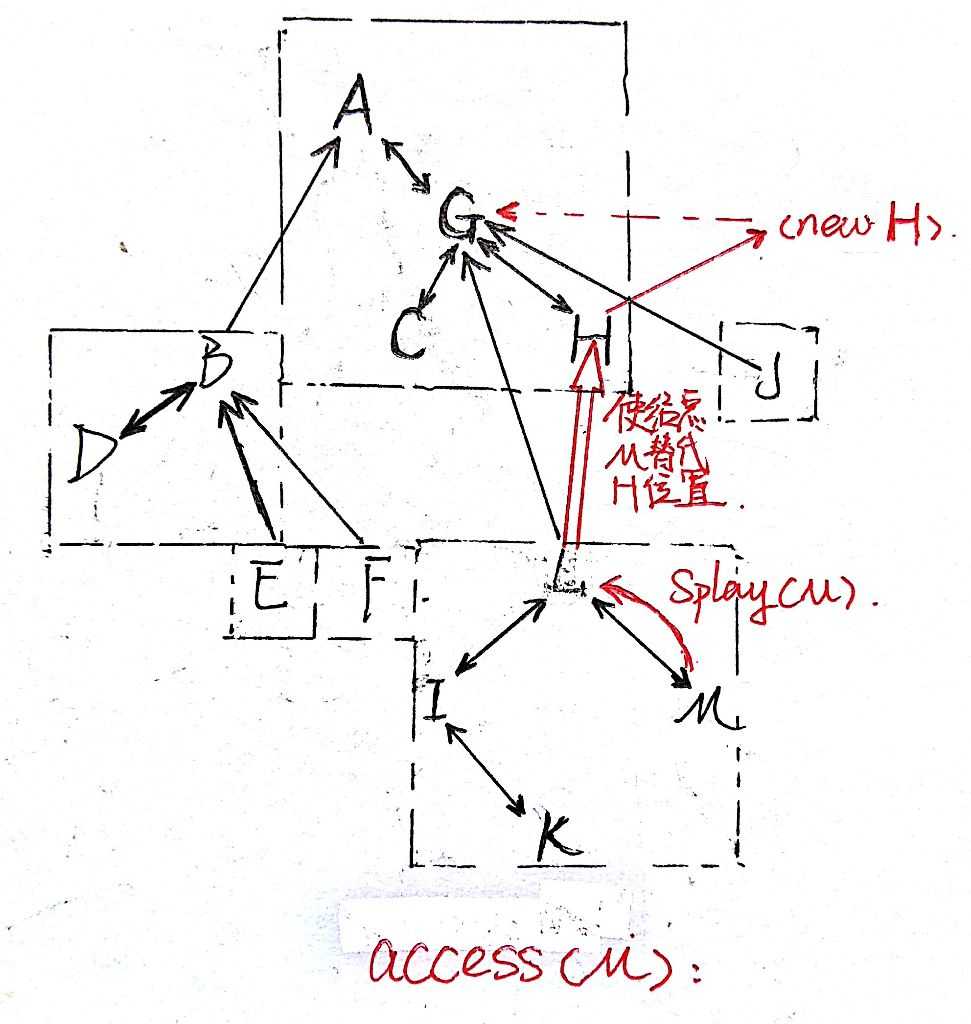
根据样例我们可以看出,access的操作大概可以分两步:
首先,Splay(M),将M旋转到Splay的根节点;
然后,使节点M替代它的父亲G的右子的位置,即G->rs=M。
这时,原本G的右子脱离了G所在的伸展树,与G连接的边变为了虚边;而节点M对应的伸展树则与G所在的伸展树合并,M和G之间的虚边变成了实边。
循环执行这两个操作,直到到达根节点,access操作就完成了。
这里需要注意的是,当完成一次连实边操作之后,需要将它的父亲pushup,以保证其维护数据的正确性。
这样,我们就得到了access的代码:

inline void access(int u) { for(int v=0;u;v=u,u=father[u]) Splay(u), rs[u]=v, pushup(u); }
2.makeroot(int u) 具体功能:令节点u成为其所在树的根节点
当我们需要两个点之间的路径信息的时候,应该怎么做?
如果其中一个点不是另一个点的祖先的话,它们是不可能在同一个Splay里面的。
这时,我们就需要makeroot函数把其中一个点搞成根节点了。执行完access(u)操作之后,u会成为所在Splay深度最大的点;然后只需要把整棵树翻转,u就是整棵树的根了。
代码如下:

inline void makeroot(int u) { access(u); Splay(u); reverse(u); }
3.split(int u,int v) 具体功能:把节点u到节点v间的路径压入到一个Splay中
有了makeroot之后,split变得超级简单:

inline void split(int u,int v) { makeroot(u); access(v); Splay(v); }
4.findroot(int u) 具体功能:查询该节点所在树的根节点编号
主要应用于判断连通性。

inline int findroot(int u) { access(u); Splay(u); pushdown(u); while(ls[u]) pushdown(u),u=ls[u]; return u; }
5.link(int u,int v)
当u-v不连通时,连一条u到v的轻边。

inline void link(int u,int v) { makeroot(u); if(findroot(v)!=u) father[u]=v; }
6.cut(int u,int v)
根据LCT的性质,我们可以发现,当makeroot(u),access(v)之后,如果存在边u-v,必须满足以下条件:
(1)u-v联通
(2)u-v在同一条Splay里有父子关系
(3)u-v在Splay的中序遍历中相邻
这样判断是否有u-v的逻辑语句就完成了,直接删除即可。
代码如下:

inline void cut(int u,int v) { makeroot(u); if(findroot(v)==u && father[u]==v && rs[u]==0) father[u]=ls[v]=0,pushup(v); }
这个伸展树比一般Splay特殊一些。它的判根、rotate操作和Splay操作之前的pushall函数需要注意一下。

int val[MAXN],ls[MAXN],rs[MAXN],father[MAXN],orsum[MAXN],size[MAXN],rev[MAXN]; inline bool isroot(int u) { return ls[father[u]]!=u && rs[father[u]]!=u; } inline void pushup(int u) { orsum[u]=val[u]^orsum[ls[u]]^orsum[rs[u]]; size[u]=1+size[ls[u]]+size[rs[u]]; } inline void reverse(int u) { if(u) { swap(ls[u],rs[u]); rev[u]^=1; } } inline void pushdown(int u) { if(rev[u]) { reverse(ls[u]); reverse(rs[u]); rev[u]^=1; } } inline void rotate(int S) { //风格比较清奇,凑活看吧qaq int u=father[S]; if(father[u]) { if(ls[father[u]]==u) ls[father[u]]=S; else if(rs[father[u]]==u) rs[father[u]]=S; } father[S]=father[u]; father[u]=S; if(ls[u]==S) { if(rs[S]) father[rs[S]]=u; ls[u]=rs[S]; rs[S]=u; } else { if(ls[S]) father[ls[S]]=u; rs[u]=ls[S]; ls[S]=u; } pushup(u); pushup(S); } void pushall(int u) { if(!isroot(u)) { pushall(father[u]); pushdown(father[u]); } } inline void Splay(int u) { pushall(u); pushdown(u); //执行操作之前先pushdown.当然也可以手写栈替代系统栈 while(!isroot(u)) { if(isroot(father[u])) rotate(u); else if((ls[father[u]]==u) == (ls[father[father[u]]]==father[u])) rotate(father[u]), rotate(u); else rotate(u), rotate(u); } }
给定n个点以及每个点的权值,要你处理接下来的m个操作。操作有4种。操作从0到3编号。点从1到n编号。
0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor和。保证x到y是联通的。
1:后接两个整数(x,y),代表连接x到y,若x到y已经联通则无需连接。
2:后接两个整数(x,y),代表删除边(x,y),不保证边(x,y)存在。
3:后接两个整数(x,y),代表将点x上的权值变成y。
这是一道裸模板题(其实也没有什么更复杂的操作了,大概就是这么回事)
注意:该pushdown就pushdown;该pushup就pushup。

/* 716ms/4835K 多维护了一个size */ #include <iostream> #include <cstdio> using namespace std; const int MAXN=300006; int val[MAXN],ls[MAXN],rs[MAXN],father[MAXN],orsum[MAXN],size[MAXN],rev[MAXN]; inline bool isroot(int u) { return ls[father[u]]!=u && rs[father[u]]!=u; } inline void pushup(int u) { orsum[u]=val[u]^orsum[ls[u]]^orsum[rs[u]]; size[u]=1+size[ls[u]]+size[rs[u]]; } inline void reverse(int u) { if(u) { swap(ls[u],rs[u]); rev[u]^=1; } } inline void pushdown(int u) { if(rev[u]) { reverse(ls[u]); reverse(rs[u]); rev[u]^=1; } } inline void rotate(int S) { int u=father[S]; if(father[u]) { if(ls[father[u]]==u) ls[father[u]]=S; else if(rs[father[u]]==u) rs[father[u]]=S; } father[S]=father[u]; father[u]=S; if(ls[u]==S) { if(rs[S]) father[rs[S]]=u; ls[u]=rs[S]; rs[S]=u; } else { if(ls[S]) father[ls[S]]=u; rs[u]=ls[S]; ls[S]=u; } pushup(u); pushup(S); } void pushall(int u) { if(!isroot(u)) { pushall(father[u]); pushdown(father[u]); } } inline void Splay(int u) { pushall(u); pushdown(u); while(!isroot(u)) { if(isroot(father[u])) rotate(u); else if((ls[father[u]]==u) == (ls[father[father[u]]]==father[u])) rotate(father[u]), rotate(u); else rotate(u), rotate(u); } } inline void access(int u) { for(int v=0;u;v=u,u=father[u]) Splay(u), rs[u]=v, pushup(u); } inline void makeroot(int u) { access(u); Splay(u); reverse(u); } inline int findroot(int u) { access(u); Splay(u); pushdown(u); while(ls[u]) pushdown(u),u=ls[u]; return u; } inline void split(int u,int v) { makeroot(u); access(v); Splay(v); } inline void link(int u,int v) { makeroot(u); if(findroot(v)!=u) father[u]=v; } inline void cut(int u,int v) { makeroot(u); if(findroot(v)==u && father[u]==v && rs[u]==0) father[u]=ls[v]=0,pushup(v); } inline int read() { char ch=getchar(); int ret=0; while(ch<‘0‘ || ch>‘9‘) ch=getchar(); while(ch>=‘0‘ && ch<=‘9‘) ret=ret*10+(ch-‘0‘), ch=getchar(); return ret; } int main() { int n=read(),m=read(),opt,x,y; for(int i=1;i<=n;i++) val[i]=orsum[i]=read(),size[i]=1; while(m--) { opt=read(); x=read(); y=read(); if(opt==0) split(x,y), printf("%d %d\n",orsum[y],size[y]); else if(opt==1) link(x,y); else if(opt==2) cut(x,y); else access(x), Splay(x), val[x]=y, pushup(x); } }
(持续更新)C++ LCT(Link-cut-tree) 动态树 总结
标签:pen 虚线 ota view 双向 包含 最短路径 原理 int
原文地址:https://www.cnblogs.com/queuDU/p/9157498.html