标签:text else class 说明 roo 父节点 body 文件 call
二叉树的遍历方式
分别为中序遍历(左子树->当前节点->右子树)、前序遍历(当前节点->左子树->右子树)、后序遍历(左子树->右子树->当前节点)。下面使用JavaScript语言实现二叉树的三种遍历算法。
首先构造一个排序二叉树(即满足左子节点比父节点小,右子节点比父节点大的二叉树),然后对其分别进行中序、前序、后序遍历。
排序二叉树结构图如下图所示:
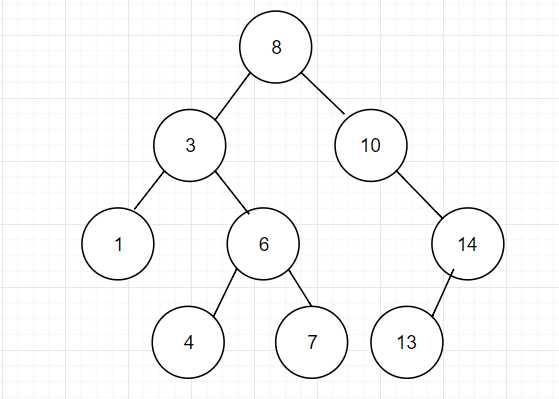
说明:
其中8为根节点(没有父节点的节点),4,、7、13为叶子节点(最后一层上没有子节点的节点),3、10、1、6、14为中间节点。
该树的最大深度为4(共4层)。
具体代码:
<!DOCTYPE html>
<html lang="en">
<head>
<title>javaScript实现二叉树算法</title>
</head>
<body>
<script type="text/javascript">
function BinaryTree(){
var Node = function(key) {//定义节点,包括父节点,左子节点,右子节点
this.key = key;//传入的元素值作为父节点
this.left = null;//左子节点初始为null
this.right = null;//右子节点初始为null
};
var root = null;//设置根节点初始值为空
// 定义插入节点函数,入参为当前节点和新加的节点
var insertNode = function(node, newNode) {
if (newNode.key < node.key) {//若新节点的父节点值小于的当前的节点的父节点值,则往左半部分走
if (node.left === null) {//当前节点若没有左子节点,则新节点作为当前节点的左子节点
node.left = newNode;
} else {//若当前节点的左子节点存在,则递归调用插入节点函数
insertNode(node.left, newNode);
}
} else {//若新节点的父节点值不小于当前节点的父节点值,则往右半部分走
if (node.right === null) {//若当前节点的右子节点不存在,则新节点作为当前节点的右子节点
node.right = newNode;
} else {//若当前节点的右子节点存在,则递归调用插入节点函数
insertNode(node.right, newNode);
}
}
};
this.insert = function(key) {//定义插入节点函数
var newNode = new Node(key);//定义新节点
if (root === null) {//若根节点为空,则新节点作为根节点
root = newNode;
} else {//若根节点存在,则执行插入节点函数
insertNode(root, newNode);
}
};
//中序遍历:左子树->当前节点->右子树,结果是一个升序有序序列
var inOrderTraverseNode = function(node, callback) {
if (node !== null) {//当前节点存在
inOrderTraverseNode(node.left, callback);//遍历左子树
callback(node.key);//执行回调函数
inOrderTraverseNode(node.right, callback);//遍历右子树
}
}
this.inOrderTraverse = function(callback) {
inOrderTraverseNode(root, callback);
}
//前序遍历:当前节点->左子树->右子树,常用于复制一个二叉树,效率高。
var preOrderTraverseNode = function(node, callback) {
if (node !== null) {//当前节点不为空
callback(node.key);//执行回调函数
preOrderTraverseNode(node.left, callback);//遍历左子树
preOrderTraverseNode(node.right, callback);//遍历右子树
}
}
this.preOrderTraverse = function(callback) {
preOrderTraverseNode(root, callback);
}
//后序遍历:左子树->右子树->当前节点,常用于文件系统遍历
var postOrderTraverseNode = function(node, callbakc) {
if (node !== null) {//当前节点不为空
postOrderTraverseNode(node.left, callback);//遍历左子树
postOrderTraverseNode(node.right, callback);//遍历右子树
callback(node.key);//执行回调函数
}
}
this.postOrderTraverse = function(callback) {
postOrderTraverseNode(root, callback);
}
}
//测试二叉树排序
var nodes = [8, 3, 10, 1, 6, 14, 4, 7, 13];
var binaryTree = new BinaryTree();//实例化一个新的二叉树
nodes.forEach(function(key) {//遍历数组中的所有元素,执行二叉树排序操作,生成排序二叉树
binaryTree.insert(key);
});
//回调函数
var callback = function(key) {
console.log(key);//打印出当前节点值
}
//中序遍历测试
binaryTree.inOrderTraverse(callback);
//前序遍历测试
binaryTree.preOrderTraverse(callback);
//后序遍历测试
binaryTree.postOrderTraverse(callback);
</script>
</body>
</html>
标签:text else class 说明 roo 父节点 body 文件 call
原文地址:https://www.cnblogs.com/stm32stm32/p/9164929.html