标签:std 数据结构 about ext efi idt i++ 通过 理解
最小生成树
首先,生成树是建立在无向图中的,对于有向图,则没有生成树的概念,所以接下来讨论的图均默认为无向图。对于一个有n个点的图,最少需要n-1条边使得这n个点联通,由这n-1条边组成的子图则称为原图的生成树。一般来说,一个图的生成树并不是唯一的(除非原图本身就是一棵树)。
现在考虑带权图G,即图的边带权,则最小生成树就是在G中权值和最小的一颗生成树,显然最小生成树也不是唯一的,但是其权值唯一。有很多应用需要用到最小生成树的概念,比较直观的一个应用就是:有n个村庄,现在要在这些村庄之间修一些路,其中村庄i和村庄j之间的距离是Dij,现在要修最短的路使得所有村庄连接起来。
显然,这个问题可以直接套用最小生成树模型,找出最小生成树即找到了一个方案。
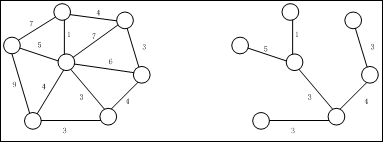
下面举一个最小生成树的例子:
对于如何寻找一个带权图的最小生成树,已经有了专门的求解方法,在具体讲解这些算法之前,我们这里先来挖掘一下最小生成树的一些特性,即一颗生成树要成为最小生成树,需要满足什么条件。
MST性质:
设一个带权无向图G(V,E,W) (V代表点集,E代表边集,W代表权值集),且T为G的一颗生成树,对于E中任意一条不属于T的边e,将其加入T中,会产生一条环(否则T不连通),如果e始终是环中权值最大的一条边,那么说明T满足MST性质。
以上是MST性质的定义,其中MST就是最小生成树的意思,但是现在并没有证明这个性质和最小生成树有什么关系,接下来将要证明,一颗生成树是最小生成树,当且仅当它满足MST性质。
引理1:对于图G(V,E,W)的两颗生成树T1和T2,若它们都满足MST性质,则它们的权值和相同。
证明:运用数学归纳法证明当有k条边在T1中而不在T2中时(0<=k<=n-1,同样的,这是也有k条边在T2中而不在T1中),T1的权值和等于T2的权值和。
1:首先,当k=0时,说明T1和T2的所有边都一样,则T1和T2是同一颗生成树,显然它们的权值和相等。
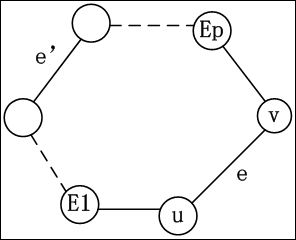
2:现在设当k<x时,T1和T2的权值和相等,现在要证明当k=x时,T1,T2权值和依然相等。考虑这样的边集S,它们在T1或T2中,但是不同时存在于T1和T2。在S中,取权值最小的那条边,设为e(u,v),不妨认为它在T1中(在T2中同理)。e连接了图中u,v两点。考虑T2中u到v之间的路径,设为E1,E2......Em(m>1),其中一定存在若干条边不在T1中(否则T1中存在环),设e‘为这些边中的一条。
(1)e’和e都属于S,所以e‘的权值不小于e。
(2)由于T2满足MST性质,且e不属于T2,那么可知e‘的权值不大于e。
综上所述,e的权值和e‘的权值相等,所以,将T2的边e‘去掉,换成e,变成T2‘,显然,T2‘和T2的权值和相等,又T2‘与T1只有x-1条边不同(即有x-1条边在T1中而不在T2中)。由归纳法可知T2‘和T1的权值和相等,所以T2和T1的权值和相等。
证毕。
有了引理1,那么MST性质和最小生成树的关系就很容易证明了。
定理1:一颗生成树T是最小生成树,当且仅当它满足MST性质。
证明:
1:最小生成树->满足MST性质
设T是G(V,E,W)的最小生成树,采用反证法,如果T不满足MST性质,那么说明存在一条边e,其不存在与T中,将其加入T中后,它不是环中权值最大的边,设环中比e还大的边为e‘,那么我们将T中的e‘去掉,换成e,得到的生成树T‘将会拥有更小的权值和,这和T是最小生成树矛盾,所以,如果T是最小生成树,则T一定满足MST性质。
2:满足MST性质->最小生成树
设T是G(V,E,W)的生成树,其满足MST性质。由1我们知道,G的最小生成树满足MST性质,再由引理1,我们知道,两颗满足MST性质的生成树权值和相等,所以T的权值和与最小生成树相等,所以T是G的一颗最小生成树。
证毕。
以上证明了最小生成树的一个关键性质,下面是时候讲解求解最小生成树的具体算法了。求解最小生成树有两个经典算法。Prim算法和Kruskal算法。下面分别介绍这两个算法的步骤和正确性证明。
Prim算法:
Prim算法基于一种贪心的思想,通过局部最优策略,每次将一条边加入所构建的生成树中,加完n-1条边后,保证最后所得的生成树是整体最优的,即最小生成树。下面简单说明下Prim算法的步骤:
Prim算法将图中的每个点分成三种状态:
第一种tree点,表示该点已经在所构造的生成树中。
第二种fringe点,表示还没在树中,但是和Tree点相邻(有一条边直接相连),是即将要加入生成树中的候选点。
第三种unseen点,其他的点,表示还没有检测到的点。
那么Prim算法步骤为:
1:初始时将所有点初始化成unseen,并且随机将一个点S设为tree点(如1号点)。
2:将所有与S相邻的点设为fringe。
3:如果图中还存在fringe点,则到4,否则到6。
4:在所有连接一个fringe点和一个tree点的边中,取权值最小的边e(u,v),不妨设u为tree点,v为fringe点,将v点设为tree点。
5:将所有与v相邻的unseen点设为fringe,并将e加入到构建的生成树中。转到3。
6 : 如果图中所有点均为tree点,则图的一个最小生成树找到。否则原图不存在最小生成树。
7:算法结束。
根据所给算法描述,很容易得到算法的代码实现,算法实现需要用到堆优化,不熟悉堆的朋友可以自行上网查询,这里不再赘述:
- struct edge{
- int to,len,next;
- }e[maxm];
- int box[maxn],cnt,used[maxn];
- void init(int n){
- for(int i=0;i<=n;i++)box[i]=-1;
- cnt=0;
- }
- void add(int from,int to,int len){
- e[cnt].to=to;
- e[cnt].len=len;
- e[cnt].next=box[from];
- box[from]=cnt++;
- }
- struct node{
- int v,len;
- node(){}
- node(int x,int y):v(x),len(y){}
- bool operator<(const node &x)const{
- return len>x.len;
- }
- };
- priority_queue<node> pq;
- int Prim(int n,int m){
- memset(used,0,sizeof(used));
- int num=0,sum=0,now=1;
- do{
- used[now]=1;
- for(int t=box[now];t+1;t=e[t].next){
- int v=e[t].to,len=e[t].len;
- if(!used[v])pq.push(node(v,len));
- }
- while(!pq.empty()){
- node tmp=pq.top();pq.pop();
- int v=tmp.v,len=tmp.len;
- if(used[v])continue;
- now=v;
- sum+=len;
- break;
- }
- num++;
- }while(num<n);
- return sum;
- }
//Prim
struct edge{
int to,len,next;
}e[maxm];
int box[maxn],cnt,used[maxn];
void init(int n){
for(int i=0;i<=n;i++)box[i]=-1;
cnt=0;
}
void add(int from,int to,int len){
e[cnt].to=to;
e[cnt].len=len;
e[cnt].next=box[from];
box[from]=cnt++;
}
struct node{
int v,len;
node(){}
node(int x,int y):v(x),len(y){}
bool operator<(const node &x)const{
return len>x.len;
}
};
priority_queue<node> pq;
int Prim(int n,int m){
memset(used,0,sizeof(used));//初始化所有点,设状态为unseen
int num=0,sum=0,now=1;
do{
used[now]=1;
for(int t=box[now];t+1;t=e[t].next){
int v=e[t].to,len=e[t].len;
if(!used[v])pq.push(node(v,len));
}
while(!pq.empty()){
node tmp=pq.top();pq.pop();
int v=tmp.v,len=tmp.len;
if(used[v])continue;
now=v;
sum+=len;
break;
}
num++;
}while(num<n);
return sum;
}
现在来看看为什么Prim算法是正确的。
首先,如果一个图存在最小生成树,那么由上面的算法得到的一定是一颗生成树。因为当算法结束时,所有的点均为tree点,说明所有点都连通。并且得到的子图不会存在环,因为我们增加一条边时,这条边连接的一定是一个tree点和一个finge点,只有连接两个tree点时才会产生环。
前面的定理1告诉我们,一颗生成树是最小生成树,那么当且仅当它满足MST性质,那么我们只要证明Prim算法得到的生成树满足MST性质即可。
定理2:设带全图G(V,E,W)存在最小生成树,那么Prim算法得到的生成树就是G的最小生成树。
证明:我们只要证明,Prim算法得到的生成树满足MST性质即可,这可由归纳法证明。下面证明,当加入第k个点时(1<=k<=n),Prim算法得到生成树满足MST性质:
1:当k=1时,只有一个点,显然满足MST性质。
2:当k>1时,我们假设当1k<x时,均满足,当k=x时,假设当前所加入的边为e(u,v),同样地,设u为tree点,v为fringe点,未加入x前的生成树为T。我们假设T+e=T‘得到的生成树不满足MST性质。既然不满足MST性质,那么一定存在一条边e‘(x,y),加入T‘后,产生的环中存在权值大于e‘的边。
如果x,y都不等于v,那么加入e‘产生的环存在于T中,但是T满足MST性质(因为T中只有x-1个点),所以x,y中一定有一个是v。不妨设y=v。
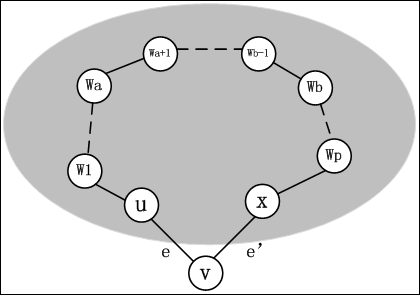
那么如下图:
如上图,设u到x之间的路径为W1......Wa,Wa+1.....Wb-1,Wb.......Wp,其中W1为u,Wp为x,设边WaWa+1是路径中第一条权值大于e‘的边,
Wb-1Wb是最后一条权值大于e‘的边(有可能这两条边是同一条)。不妨设WaWa+1先于Wb-1Wb加入到T中,那么由Prim算法的步骤,知W1W2,W2W3.......Wa-1Wa均会先于WaWa+1加入到T‘中,进一步由于e先于e’加入到T中,所以有|e|<=|e‘|<|Wb-1Wb|,所以e和e‘均会先于WaWa+1加入到T‘中,但是事实是,e‘并不在T‘中,而且它比WaWa+1要晚加入T‘中,所以矛盾。所以T‘加入e‘后,所产生的环中e‘的权值最大,满足MST性质。那么当k=n的时候,也就是算法完成的时候,所得到的生成树就是整个图G的生成树,它满足MST性质,由定理1可知,它是最小生成树。证毕。
Kruskal算法:
Kruskal算法同样是基于贪心策略,但是它和Prim算法不同的是,在算法过程中它并不维护一个连通的分量,而是将多个连通分量合并到一起得到一颗生成树。个人觉得Kruskal算法的思想比它算法本身要重要,能够解决很多其他问题,至少是在ACM比赛中吧。
下面描述一下Kruskal算法的步骤:
首先将图中的所有的边按照其权值从小到大排序,然后从小到大枚举边。设需要构造的生成树为T。
1:初始时,T中没有变,所有点看成是一个单独的集合。
2:如果枚举完最后一条边,则到4,否则到3。
3:设当前枚举的边为e(u,v),如果u,v不在同一个集合中,则将e加入到T中,并且将u和v合并到一个集合中,否则,忽略e。转到2.
4:如果T中含有n-1条边,则说明找到原图的最小生成树,否则说明原图没有最小生成树。算法结束。
算法的实现需要一些额外的知识,首先是要从小到大枚举边,这里可以用快速排序直接将边集排序,或者可以用小顶堆来初始化边集。
然后是要判断两个点是否在统一集合中,还需要将两个集合合并到一个集合中。这里要用到并查集这一数据结构。这方面的知识请自行参考相关资料。
下面是利用快速排序和并查集实现的Kruskal算法。
- #define maxn 110
- #define maxm 10010
- using namespace std;
- int uf[maxn];
- struct edge{
- int u,v,len;
- }e[maxm];
- bool cmp(const edge &x,const edge &y){
- return x.len<y.len;
- }
- void init(int n){
- for(int i=0;i<=n;i++)uf[i]=i;
- }
- int find(int x){
- if(x==uf[x])return x;
- return uf[x]=find(uf[x]);
- }
- int Union(int x,int y){
- x=find(x),y=find(y);
- if(x!=y){
- uf[x]=y;
- return 1;
- }
- return 0;
- }
- int Kruskal(int n,int m){
- sort(e,e+m,cmp);
- int sum=0;
- for(int i=0;i<m;i++){
- int u=e[i].u,v=e[i].v,len=e[i].len;
- sum+=len*Union(u,v);
- }
- return sum;
- }
#define maxn 110
#define maxm 10010
using namespace std;
int uf[maxn];
struct edge{
int u,v,len;
}e[maxm];
bool cmp(const edge &x,const edge &y){
return x.len<y.len;
}
void init(int n){//初始化并查集
for(int i=0;i<=n;i++)uf[i]=i;
}
int find(int x){
if(x==uf[x])return x;
return uf[x]=find(uf[x]);
}
int Union(int x,int y){//合并两个集合(如果x,y在同一集合,返回0,否则返回1)
x=find(x),y=find(y);
if(x!=y){
uf[x]=y;
return 1;
}
return 0;
}
int Kruskal(int n,int m){//n个点,m条边
sort(e,e+m,cmp);//排序
int sum=0;//最小生成树的权值和
for(int i=0;i<m;i++){//从小到大枚举边
int u=e[i].u,v=e[i].v,len=e[i].len;
sum+=len*Union(u,v);
}
return sum;//返回权值和
}
Kruskal算法的正确性
同Prim算法正确性证明一样,我们只要证明Kruskal算法得到的生成树满足MST性质即可。首先,如果G存在最小生成树,那么Kruskal算法得到肯定是一颗生成树。这点就不证明了,用反证法可以很容易证明。
定理3:设带全图G(V,E,W)存在最小生成树,那么Kruskal算法得到的生成树就是G的最小生成树。
证明:设Kruskal算法结束时得到的生成树为T,假设T不满足MST性质,那么存在一条边e(u,v),它不属于T,将e加入T中后,得到一个环。设环中存在一条(可能是多条)边e‘,其权值大于e。那么由Kruskal算法的步骤,可知,e在e‘之前枚举。当枚举e‘之前,可知u,v一定不在同一个集合中,否则e‘就不会在T中了。那么既然在e‘加入之前,u,v不在同一个集合中,那么枚举e时(e在e‘加入前被枚举),根据Kruskal算法的步骤3,可知e一定在T中,但是e并不在T中,矛盾,所以加入e后,所得到的环中e的权值最大。这就表示T满足MST性质。从而由定理1,可知T是G的一颗最小生成树。证毕。
总结:到此为止,最小生成树的总结就写完了,介绍的两个算法都是基于贪心思想的应用。个人觉得学习算法一定不能仅仅记住算法的代码实现,一定还要理解其中的思想和正确性。只有这样才能真正了解一个算法的精髓。就算是忘了代码的实现,理解了思想也能自己推出来。这应该才是学习的不二法门吧。
最小生成树之Prim Kruskal算法(转)
标签:std 数据结构 about ext efi idt i++ 通过 理解
原文地址:https://www.cnblogs.com/lyxcode/p/9176020.html