标签:max 优势 IV img inf 选择 com 深度网络 数据驱动
流程:模型族->算法族->深度网络->深度学习
模型族:模型中含有超参数,给予不同的参数对应不同的模型,就形成了模型族
算法族:每一个模型对应一个完整算法,整个模型族对应了一个算法族 将算法族展开成一个深度网络,网络层数代表迭代次数,模型的超参数成为网络中的参数(如权重等)。利用少量标记数据就可以训练网络。
相对于模型驱动算法的优势:
1、可以学习模型超参数,提高了模型的适应能力,提高精度
相对于数据驱动的优势:
1、网络的设计有模型指导
2、减少了数据需求量
3、减小了训练时间
比如核磁共振重建的ADMM算法:
模型:
\(x^*={arg\max}_{x}{\{\frac{1}{2}||Ax-y||^2+\sum_{l=1}^{L}\lambda_{l}g(D_{l}x)\}}\)
ADMM算法求解:
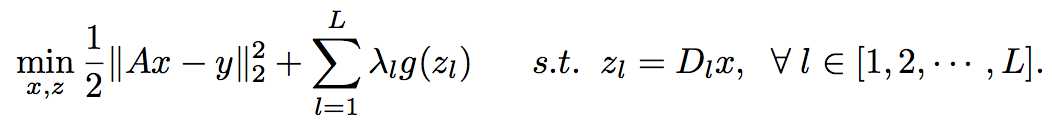
\(g,\lambda,L,D_{l}\)的不同选择形成了不同的模型,构成了模型族。
广义拉格朗日函数:
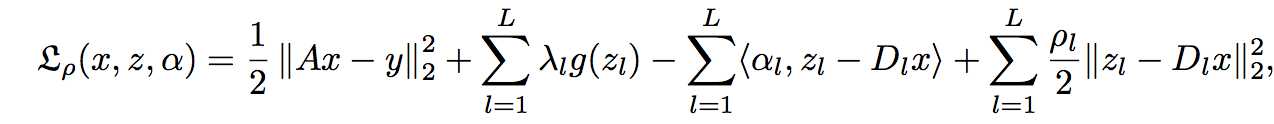
ADMM算法迭代更新过程:
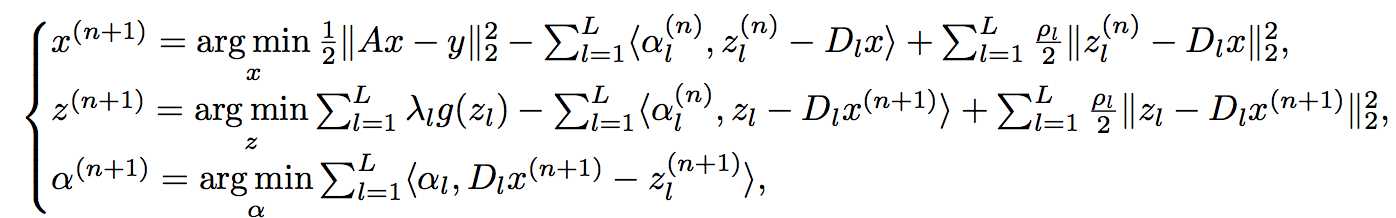
令\(\beta_{l}=\frac{\alpha_{l}}{\rho_{l}},A=PF\)(已知),可得
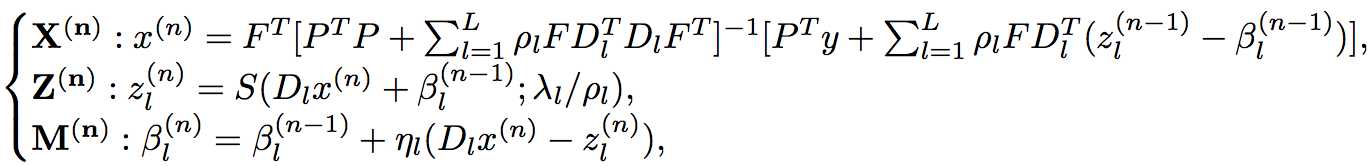
\(S(\cdot)\)是一个非线性shrinkage function。\(S(\cdot)\)通常是一个光滑函数。
网络结构:
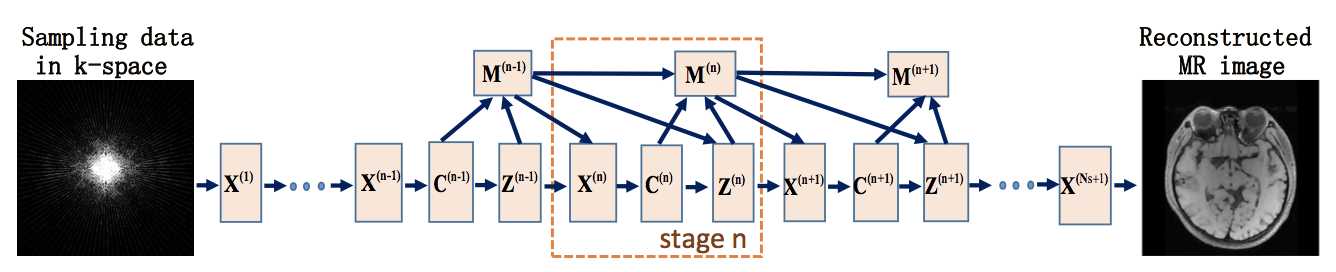
包括重建层\(X^{(n)}\)、卷积层\(C^{(n)}=D_{l}x^{(n)}\)、非线性变换层\(Z^{(n)}\)、乘子更新层\(M^{(n)}\),其中非线性变换函数\(S\)可以用分段线性函数近似,只需学习插值点的函数值即可。
网络学习的参数:模型族中的超参数,每一层可以不一样。
网咯训练:
损失函数为
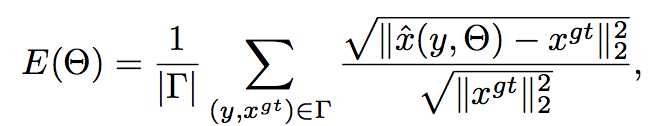
梯度下降法训练。
参考文献:
yangyan,sunjian,lihuibin,xuzongben, Deep ADMM-Net for Compressive Sensing MRI (NIPS2017)
https://arxiv.org/abs/1705.06869
标签:max 优势 IV img inf 选择 com 深度网络 数据驱动
原文地址:https://www.cnblogs.com/XiangGu/p/9190647.html