LeNet

标签：特点   窗口   size   AC   计算   function   资源   包含   UNC   

LeNet

模型特点

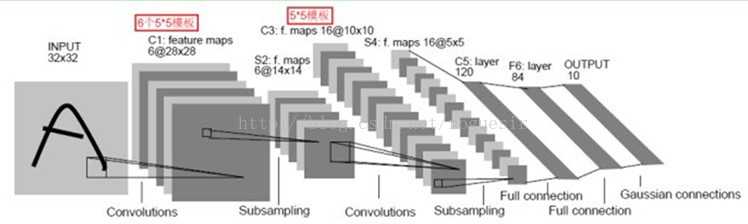
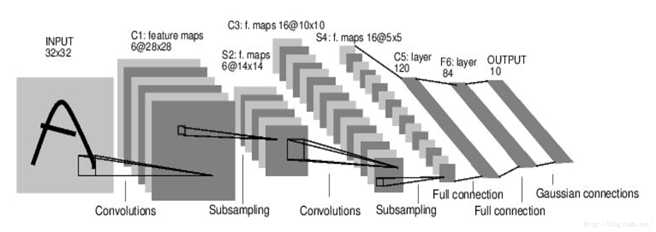
                                              图1-1 LeNet结构示意

网络层介绍

对于卷积层，其计算公式为

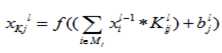
其中K表示由L层到L+1层要产生的feature的数量，表示“卷积核”，表示偏置，也就是bias，

令卷积核的大小为5*5，总共就有6*（5*5+1）=156个参数，

对于卷积层C1，每个像素都与前一层的5*5个像素和1个bias有连接，

所以总共有156*28*28=122304个连接（connection）。

对于LeNet5，S2这个pooling层是对C1中的2*2区域内的像素求和再加上一个偏置，

然后将这个结果再做一次映射（sigmoid等函数），所以相当于对S1做了降维，此处共有6*2=12个参数。

S2中的每个像素都与C1中的2*2个像素和1个偏置相连接，所以有6*5*14*14=5880个连接（connection）。

除此外，pooling层还有max-pooling和mean-pooling这两种实现，

max-pooling即取2*2区域内最大的像素，而mean-pooling即取2*2区域内像素的均值。

LeNet5最复杂的就是S2到C3层，其连接如下图所示。

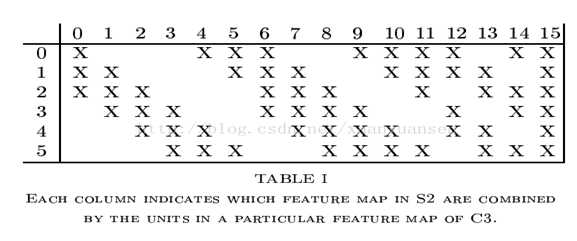
前6个feature map与S2层相连的3个feature map相连接，

后面6个feature map与S2层相连的4个feature map相连接，

后面3个feature map与S2层部分不相连的4个feature map相连接，

最后一个与S2层的所有feature map相连。

卷积核大小依然为5*5，

所以总共有6*（3*5*5+1）+6*（4*5*5+1）+3*（4*5*5+1）+1*（6*5*5+1）=1516个参数。

而图像大小为10*10，所以共有151600个连接。

S4是pooling层，窗口大小仍然是2*2，共计16个feature map，

所以32个参数，16*（25*4+25）=2000个连接。

C5是卷积层，总共120个feature map，每个feature map与S4层所有的feature map相连接，卷积核大小是5*5，

而S4层的feature map的大小也是5*5，所以C5的feature map就变成了1个点，共计有120（25*16+1）=48120个参数。

F6相当于MLP中的隐含层，有84个节点，所以有84*（120+1）=10164个参数。

F6层采用了正切函数，计算公式为，

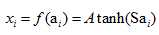
输出层采用了RBF函数，即径向欧式距离函数，计算公式为，

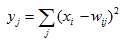
以上就是LeNet5的结构。

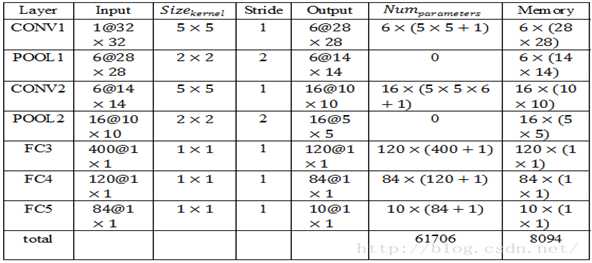
表1 LeNet各层输入输出及资源使用

LeNet

标签：特点   窗口   size   AC   计算   function   资源   包含   UNC   

原文地址：https://www.cnblogs.com/wangprince2017/p/9192060.html