标签:旋转 就会 多个 树结构 深度 style 左右子树 集合 一个
1.简单地认识下与索引有关的数据结构: 树的简单概念:由n个节点组成具有层次关系的集合,根朝上叶朝下 树的特点:每个节点有0或多个子节点,无父节点称为根节点,每个非根节点有且只有一个父节点,每个节点可分为多个不相交的子树(父节点除外)
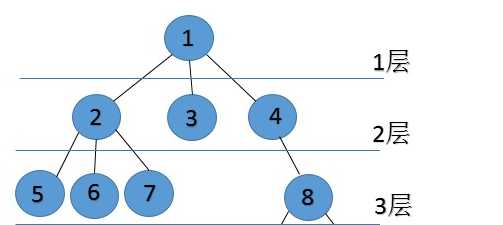
二叉树的简单概念:每个节点最多有2个子树的树结构,有左右子树之分
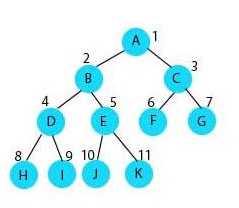
二叉查找树的简单概念:二叉树的前提下,左子树上所有节点的值均小于/等于其父节点的值,右子树上所有几点的值均大于/等于其父节点的值,左右子树也分别为二叉查找树
二叉查找树的查找步骤:小于往左,大于往右,相等则查找成功,子树为空不成功
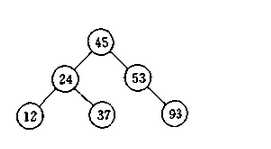
但是,二叉查找树遇到以下的情况效率会很低
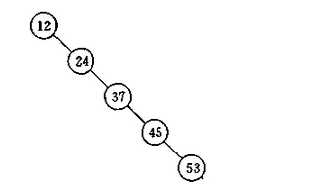
存在某一节点高度过高
就有了平衡二叉树的存在 二叉平衡树的简单概念:在二叉查找树的前提下,任何节点的两棵子树的高度最大差为1(|BF|<=1) 平衡因子(BF):BF=左子树深度—右子树深度 要维持二叉平衡树的平衡,最为重要的是找到其最小不平衡树,最小不平衡树可以这样来找:找距离插入节点最近且平衡因子的绝对值大于1的结点为根的子树,找到最小不平衡树之后呢,需要将其变为平衡,主要是依靠旋转来实现的 如何维持平衡(3种最小不平衡树,3种旋转方式): a.左旋:BF< -1时,父节点变为该节点的左节点 b.右旋:BF> 1时,父节点变为该节点的右节点 c.左旋+右旋 or 右旋+左旋:插入节点后,最小不平衡树的BF与它的子树的BF符号相反时,依具体情况先旋转一次使符号相同后,再反向旋转一次
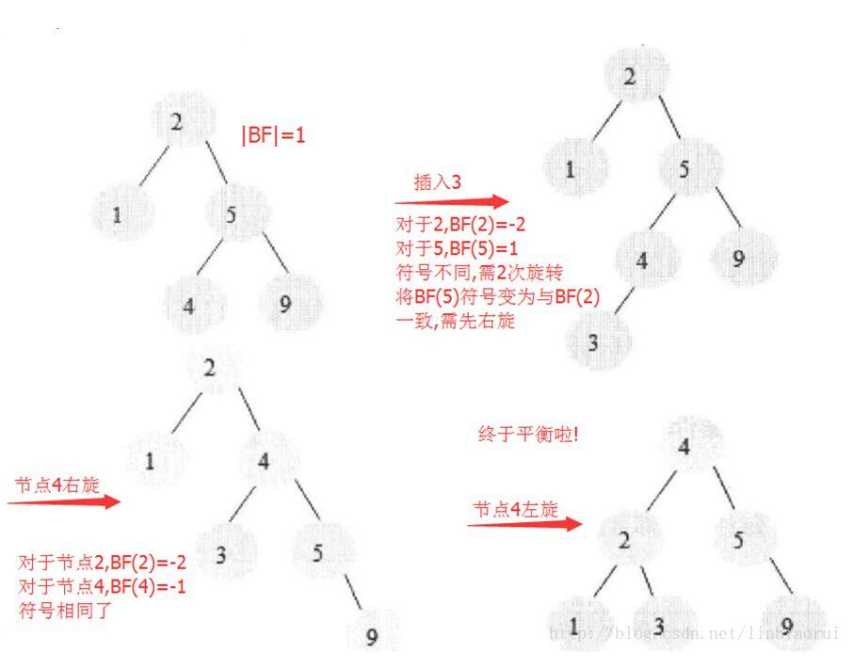
但是,二叉树每一个节点最多也就对应2个子节点,节点一多的话树的高度就会很大,查找起来要遍历的层数会很多,效率还是个问题,于是,B+树便应运而生了 。
B+树的简单概念:一种特殊的平衡查找树,所有记录节点都是按键值大小顺序存放于同一层的叶子节点,各叶子节点以指针进行衔接,键值小在左,键值大在右 。
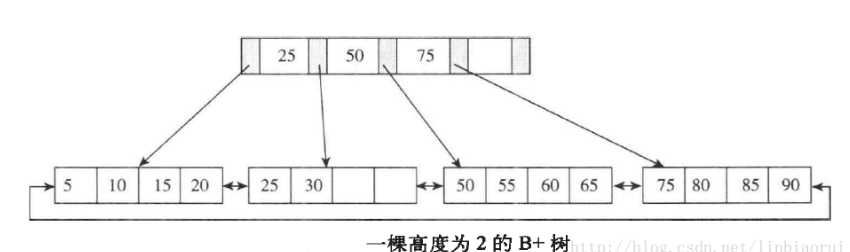
叶子节点从左到右顺序遍历便可得到所有键值的顺序排序,这也是为什么联合索引需满足“最左前缀匹配”的原因。
标签:旋转 就会 多个 树结构 深度 style 左右子树 集合 一个
原文地址:https://www.cnblogs.com/cbxBlog/p/9192895.html