标签:辅助 存在 image 技术 info 复杂度 结果 顶点 alt
这里介绍 Dijkstra 算法,它是一个应用最为广泛的、名气也是最大的单源最短路径算法Dijkstra 算法有一定的局限性:它所处理的图中不能有负权边
「前提:图中不能有负权边」
换句话说,如果一张图中,但凡有一条边的权值是负值,那么使用 Dijkstra 算法就可能得到错误的结果不过,在实际生活中所解决的问题,大部分的图是不存在负权边的
如:有一个路线图,那么从一点到另外一点的距离肯定是一个正数,所以,虽然 Dijkstra 算法有局限性,但是并不影响在实际问题的解决中非常普遍的来使用它
看如下实例:
(1)初始

左边是一张连通带权有向图,右边是起始顶点 0 到各个顶点的当前最短距离的列表,起始顶点 0 到自身的距离是 0
(2)将顶点 0 进行标识,并作为当前顶点
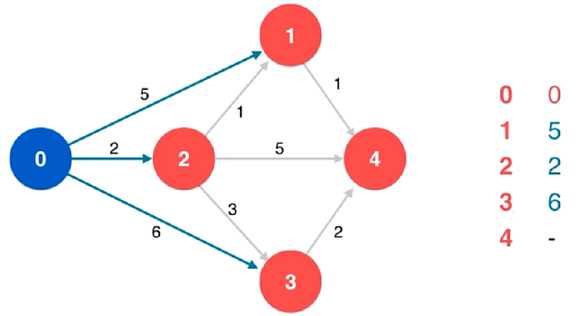
对当前顶点 0 的所有相邻顶点依次进行松弛操作,同时更新列表从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 2,就可以说,起始顶点 0 到顶点 2 的最短路径即 0 -> 2
因为:图中没有负权边,即便存在从顶点 1 到顶点 2 的边,也不可能通过松弛操作使得从起始顶点 0 到顶点 2 的距离更小
图中没有负权边保证了:对当前顶点的所有相邻顶点依次进行松弛操作后,只要能从列表的未标识顶点中找到当前最短距离最小的顶点,就能确定起始顶点到该顶点的最短路径
(3)将顶点 2 进行标识,并作为当前顶点
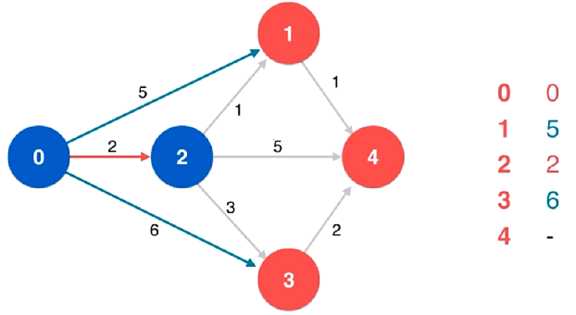
(4)对当前顶点 2 的相邻顶点 1 进行松弛操作,同时更新列表
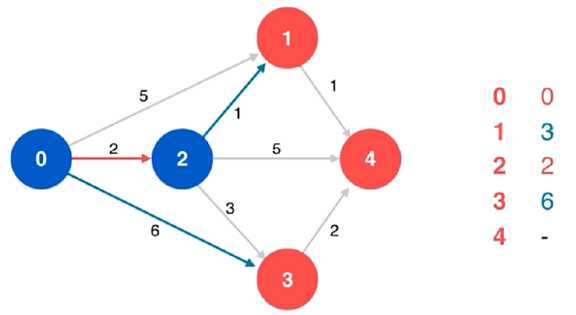
(5)对当前顶点 2 的相邻顶点 4 进行松弛操作,同时更新列表
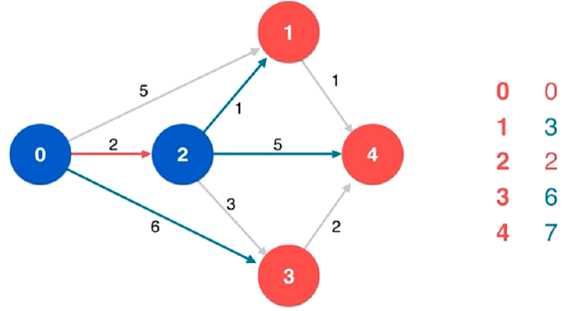
(6)对当前顶点 2 的相邻顶点 3 进行松弛操作,同时更新列表
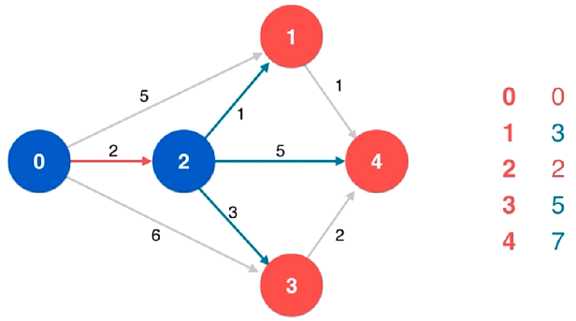
从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 1,
就可以说,起始顶点 0 到顶点 1 的最短路径即 0 -> 2 -> 1
(7)将顶点 1 进行标识,并作为当前顶点
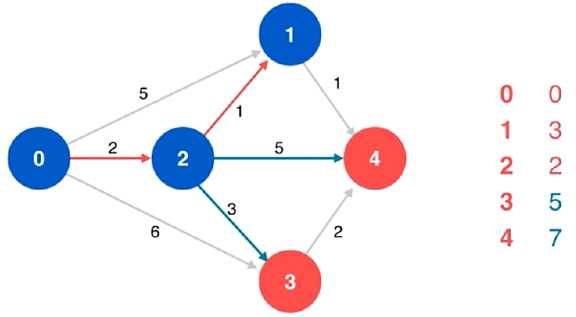
(8)对当前顶点 1 的相邻顶点 4 进行松弛操作,同时更新列表
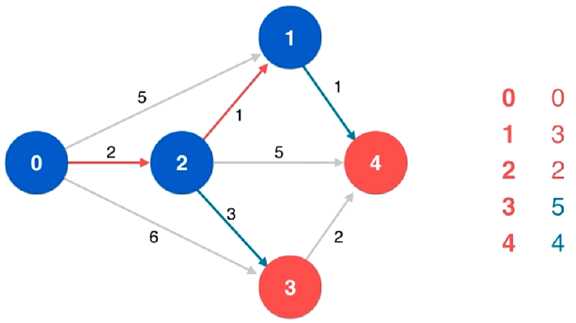
从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 4,就可以说,起始顶点 0 到顶点 4 的最短路径即 0 -> 2 -> 1 -> 4
(9)将顶点 4 进行标识,并作为当前顶点
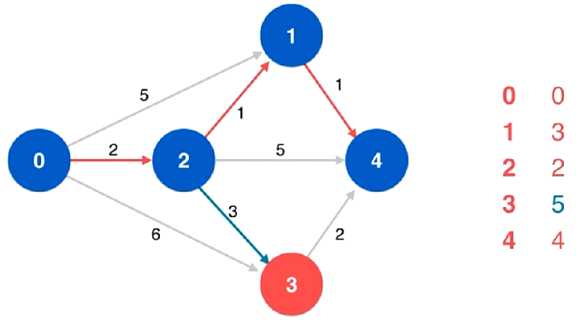
当前顶点 4 没有相邻顶点,不必进行松弛操作
从列表的未标识顶点中找到当前最短距离最小的顶点,即 顶点 3,就可以说,起始顶点 0 到顶点 3 的最短路径即 0 -> 2 -> 3
(10)将顶点 3 进行标识,并作为当前顶点
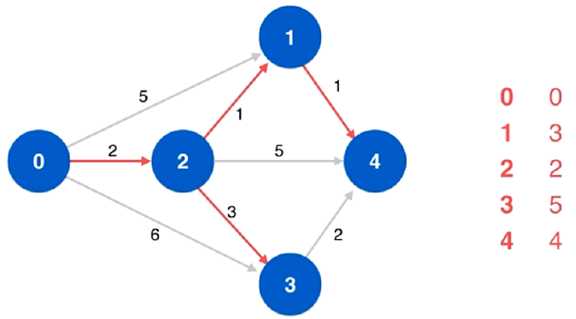
对当前顶点 3 的相邻顶点 4 进行松弛操作,发现不能通过松弛操作使得从起始顶点 0 到顶点 4 的路径更短,所以保持原有最短路径不变至此,列表中不存在未标识顶点,Dijkstra 算法结束,找到了一棵以顶点 0 为根的最短路径树
Dijkstra 算法的过程总结:
第一步:从起始顶点开始
第二步:对当前顶点进行标识
第三步:对当前顶点的所有相邻顶点依次进行松弛操作
第四步:更新列表
第五步:从列表的未标识顶点中找到当前最短距离最小
的顶点,作为新的当前顶点
第六步:重复第二步至第五步,直到列表中不存在未标识顶点
Dijkstra 算法主要做两件事情:
(1)从列表中找最值
(2)更新列表
显然,借助最小索引堆作为辅助数据结构,就可以非常容易地实现这两件事情
最后,Dijkstra 算法的时间复杂度:O(E*logV)
标签:辅助 存在 image 技术 info 复杂度 结果 顶点 alt
原文地址:https://www.cnblogs.com/littlewrong/p/9196060.html