标签:适用于 样本 数值 table auc 引用 曲线 img 之间
线性回归的输入变量和输出变量都是连续的,逻辑回归的输入变量是连续的,输出变量是类别(或者说是离散的、枚举的)。
SVM和LR一般都用于处理分类问题,不同的是二者的实现原理,SVM是以支持向量到分类平面的距离最大化为优化目标,得到最优分类平面,LR是把输出类别以概率的方式表示,常用的是logistic sigmoid函数,然后通过极大似然或其他方法来构造最优化目标,进而求解得到最优参数。
[补充:有一个大厂的面试官提示我说,sigmoid是函数族,不是单个函数,用在LR里的是 Logistic Sigmoid函数。关于sigmoid函数族,我还没明白是什么意思。]
二者最大的区别在于是否可以把特征系数将为0,一阶惩罚项不仅可以降低模型复杂度,还可以同时完成特征筛选,即,把部分特征的系数降为0,二阶惩罚项可能会把部分特征的系数降到很小,但一般不会将特征的系数降为0。
适用的场合暂时还没有答案。
常用的指标有:准确率(precision)、召回率(recall)、F值(F-score)、AUC(Area Under ROC Curve)。
分类问题根据预测值和真实值可以分为如下四类:
| 预测值 | |||
| Positive | Negative | ||
| 真实值 | Positive | TP | FN |
| Negative | FP | TN | |
解释:
TP:True Positive,模型预测是正例,并且预测正确;
FP:False Positive,模型预测是正例,但是预测错误;
TN:True Negative,模型预测是反例,并且预测正确;
FN:False Negative,模型预测是反例,但是预测错误。
TP FP TN FN 分别表示四个类别的测试样本数量,由这四个数值可以计算出:
Precision (P) = TP/(TP+FP) 解释:预测为正例的所有样本中,预测正确的占多大比例,归纳成一个字就是——“准”,因此也称为查准率。
Recall (R) = TP/(TP+FN) 解释:真实是正例的所有样本中,被预测出来的占多大比例,归纳成一个字就是——“全”,因此也称为查全率。
F = 2*P*R/(P+R) 解释:P和R的调和平均。
一般来说,P和R是不可兼得的,P越高R越低,反之亦然。如果我们想要同时获得尽量高的P和R,可以用F值作为评价指标。F值本质上是P和R的调和平均,如果对P和R有不同的倾向,可以在公式中加入权重。
此外,P-R曲线也可以用来评估模型性能。我们利用模型对所有测试样本打分,得分越高表示该样本是正例的概率越高,按照得分由大到小对测试样本排序,然后从头至尾,依次预测每个样本是正例,计算此时的P和R,便可以得到P-R曲线。
引用周志华老师的图:
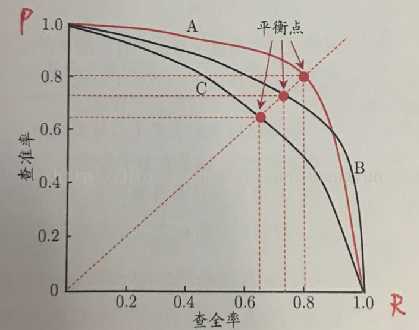
左上方的点,表示的是得分很高的测试样本的P和R,因为得分高,所以大多数是预测正确的,因此P很高,同时因为样本数量少,R很低,随着样本数量增加,R逐渐增加,P则逐渐减小,直到曲线走到右下角的位置,所有样本都被预测为正例,R一定是1,但是P很低。[补充:曲线的右下角不应该在 (0,1),应该在(p1,1)处,p1很小,这是个人的理解。]
这是个非常重要的问题,面试中最起码被问过三次,因为这个指标是分类问题中最常用的评价指标。
ROC曲线和P-R曲线的构造思想比较相近,只是横纵坐标不同。同样是根据每个测试样本的得分(实值或概率值均可)按从大到小排序,然后从头至尾,逐个预测每个样本是正例,计算 TPR 和 FPR,再把TPR和FPR连接起来,就得到了ROC曲线。
TPR (True Positive Rate) = TP/(TP+FN) 解释:就是查全率。
FPR (False Positive Rate) = FP/(FP+TN) 解释:和查全率类似,把反例当做正例,相当于反例的查全率。
再次引用周老师的图:
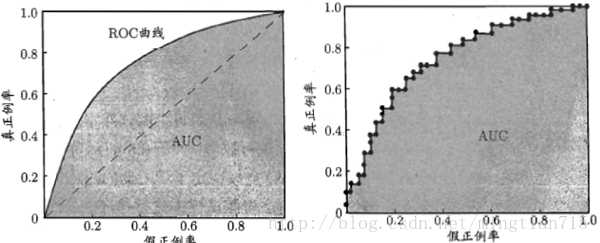
左图是理想的ROC曲线,右图是实际应用时得到的ROC曲线。曲线从左下角开始,这时测试样本数量很少,因此TPR和FPR都很小,随着样本数量增加,二者同步增加。更加的理想的情况是,TPR增加的快,FPR增加的慢,即,模型找到的正例更多,反例更少,这就对应了图中更靠上方的点,理解了这一点有助于理解AUC。样本全部判定为正例时,达到了ROC的右上角位置,此时所有正例和所有反例都被找出来了,所以TPR和FPR都是1.0。
ROC曲线和P-R曲线一样,如果模型A的ROC曲线能包裹住模型B的ROC曲线,说明模型A更优。如果模型A和模型B的ROC曲线有交叉,仍要对比二者,就可以用AUC,即ROC曲线下方的面积。AUC越大,模型越好。
[个人见解] 如果两个模型的ROC曲线有交叉,那么它们的AUC可能差距不大,比如一个是0.900,一个是0.901,此时硬说AUC略大的模型更优并没有太大意义。
ROC曲线有明确的起点和终点,分别是(0,0)和(1,1),所以AUC最大只能是1,最小是0,连接起点和终点的直线是AUC为0.5的分界线,这条线表示测试样本中正例和反例成对出现,相当于随机猜测。只要模型比随机猜测更好,AUC就应该大于0.5。
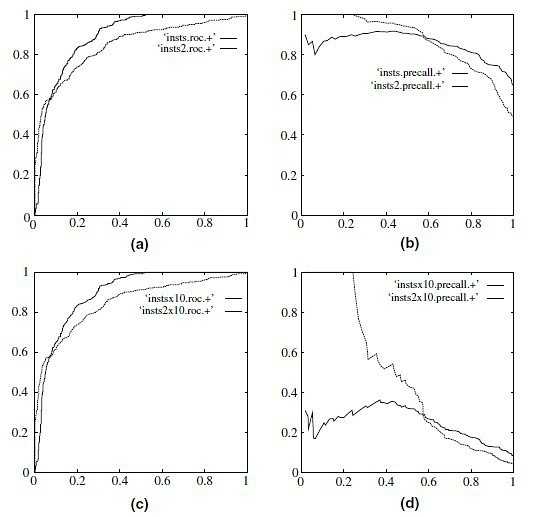
ROC曲线和P-R曲线是什么关系? 参考 豆瓣文章,P-R曲线和ROC曲线本质上是一一对应的关系,相对来看,P-R曲线比ROC曲线更能反应出模型的性能,这是因为样本存在类别不平衡问题。我们设想一下,如果样本中的正例特别少,反例特别多,对ROC曲线的主要影响是,TPR很可能早早就达到了1,使得ROC曲线的右半部分的纵坐标都是1.0,形如下图的(a)和(c)中颜色较深的曲线,对P-R曲线的影响很大,正例非常少,可能导致P一直很低或快速降低(因为预测正确并不容易),R则较快的到达接近1的位置,类似图(d)中的两条曲线的样子,这时,使用P-R曲线更能明显的反应出不同的模型的性能。 有一篇参考文献可以阅读: The Relationship Between Precision-Recall and ROC Curves ,尚未阅读,先在这留个名。
[关于两条曲线关系的理解还很浅,缺少更深入的调研和实践,先写在这里,供日后被拍砖。]
标签:适用于 样本 数值 table auc 引用 曲线 img 之间
原文地址:https://www.cnblogs.com/xxiaolige/p/9090641.html