标签:建立 ret 函数 IV 折半插入排序 pre 过多 折半查找 额外
第八章《排序》
一、直接插入排序
//直接插入排序 //算法思想:每趟将一个待排的关键字按照其值的大小插入到已经排好的部分有序序列的适当位置上,直到所有待排关键字都被插入到有序序列中为止。
//(1)时间复杂度分析:
// ①最坏情况(整个序列逆序):O(n2)
// ②最好情况(整个序列有序):O(n)
// ③平均时间复杂度:O(n2)
//(2)空间复杂度分析:
// ①:O(1)
void InsertSort(int R[], int n) //待排关键字存储在R[]中,默认为整型,个数为n { int i,j; int temp; for(int i= 1; i<n; i++) //无序列表中挑选元素 { temp=R[i]; //将带插入关键字暂存于temp中 j=i-1; while(j>0 && temp < R[j]) //循环完成从待排关键字之前的关键字开始扫描,如果大于待排关键字,则后移一位 { R[j+1] = R[j]; --j; } R[j+1] = temp; //将temp中暂存的待排关键字插入到正确位置 } }
二、折半插入排序
//折半插入排序 //算法思想:数据本身有序的前提下,取数据中间的元素与待插入元素进行对比,若待插入元素大于中间元素,则右半部分重复相同查找插入操作;若待插入元素小于中间元素,则左半部分重复相同查找插入操作;以此类推,直到插入待插入元素。 //(1)时间复杂度分析: // ①最坏情况(整个序列逆序):O(n2) // ②最好情况(整个序列有序):O(nlog?n) // ③平均时间复杂度:O(n2) //(2)空间复杂度分析: // ①:O(1) void BInsertSort(int a[],int size) { int i,j,low = 0,high = 0,mid; int temp = 0; for (i=1; i<size; i++) { low=0; high=i-1; temp=a[i]; //采用折半查找法判断插入位置,最终变量 low 表示插入位置 while (low<=high) { mid=(low+high)/2; if (a[mid]>temp) { high=mid-1; } else { low=mid+1; } } //有序表中插入位置后的元素统一后移 for (j=i; j>low; j--) { a[j]=a[j-1]; } a[low]=temp;//插入元素 } }
三、希尔排序

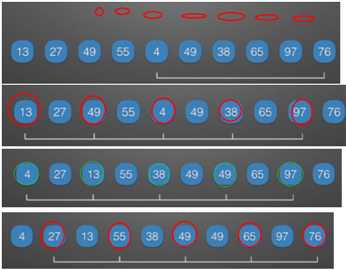
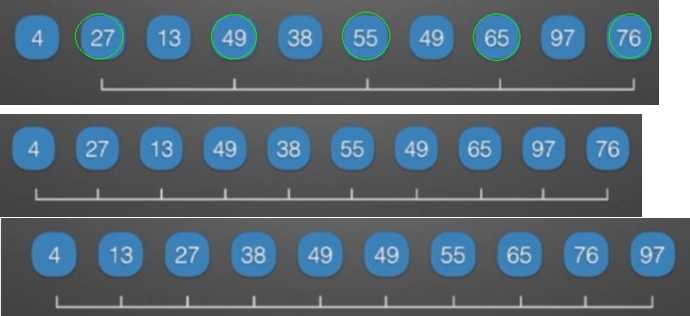
//希尔排序 //算法思想:以增量来分割整个序列,将分割的各组进行直接插入排序,然后继续相同操作直到最后以增量1分割整个序列,其实就是对整个序列进行一趟直接插入排序,从而完成整个希尔排序。 //(1)时间复杂度分析:与增量的选取有关 // ①希尔自己提出的(每次除以2,并向下取整):O(n2) // ②2^k+1,且小于待排序列长度:O(n^1.5) // ③选取增量需注意:1.增量序列的最后一个值一定取1 // 2.增量序列中的值应尽量没有除1之外的公因子 //(2)空间复杂度分析: // ①:O(1) viod shellSort(int arr[],int n) { int temp; for(int gap=n/2;gap>0;gap/=2) { for(int i=gap;i<n;++i) { temp=arr[i]; int j; for(j=i;j>=gap && arr[j-gap]>temp;gap/=2) //每个元素与自己组内的数据进行直接插入排序 arr[j]=arr[j-=gap]; arr[j]=temp; } } }
四、冒泡排序
//冒泡排序 //算法思想:【把数据降序】第一个元素和第二个元素比较,若果第一个大则二者交换,否则不交换;然后第二个元素和第三个元素比较。。。。以此类推,最终最大的元素被换到了最后面,完成一趟冒泡排序,经过多躺这样的排序,最终整个序列完成降序操作。 //结束标志是:一趟排序过程中没有发生元素交换。 //(1)时间复杂度分析: // ①最坏情况(整个序列逆序):O(n2) // ②最好情况(整个序列有序):O(n) // ③平均时间复杂度:O(n2) //(2)空间复杂度分析: // ①:O(1) void BubbleSort(int R[],int n) //默认待排序元素为整型 { int i,j; int flag; int temp; for(i=n-1;i>=1;--i) //无序序列范围(逐渐较少) { flag=0; //变量flag用来标记本趟排序是否放生了交换 for(j=1;j<=i;++j) //交换。若为0,前面没有元素,无意义 if(R[j-1]>R[j]) { temp=R[j]; R[j]=R[j-1]; R[j-1]=temp; flag=1; } if(flag==0) return; } }
五、快速排序
//快速排序 //算法思想:①取第一个元素P(此时留下一个空位),先从右往左找比P元素的小的元素,找到后把该元素放到左边的空位(此时右边留下一个空位),然后在从左往右找比P元素大的元素,找到后把该元素放到右边的空位(此时左边又留下一个空位),以此类推,使元素p归位; // ②列表被p分成两部分,左边都比p小,右边都比p大; // ③P两侧用同样的方式递归完成最终的排序。 //(1)时间复杂度分析: // ①最坏情况(整个序列逆序):O(n2) // ②最好情况(整个序列有序):O(nlog2?n) // ③平均时间复杂度:O(nlog2?n) //(2)空间复杂度分析: // ①:O(log2?n):递归需要栈的辅助 viod QuickSort(int R[],int low,int high) //对从R[low]到R[high]的元素进行排序 { int temp; int i=low,j=high; if(low<high) { temp=R[low]; while(i!=j) //循环完成一趟排序,即将数组中小于temp的元素放在左边,大于temp的元素放在右边 { while(j>i && R[j]>temp) //从右往左扫描,找到一个小于temp的元素 j--; if(i<j) { R[i]=R[j]; //放在temp的左边 ++i; //i右移一位 } while(i<j && R[i]<temp) //从左往右扫描,找到一个大于temp的元素 ++i; if(<j) { R[j]=R[i]; //放在temp的右边 --j; //j右移一位 } } R[i]temp; //将temp放在最终位置 QuickSort(R,low,i-1); //递归的对temp左边的元素进行排序 QuickSort(R,i+1,high); //递归的对temp右边的元素进行排序 } }
六、简单选择排序
//简单选择排序 //算法思想:从头到尾顺序扫描序列,找出一个最小的元素和第一个元素进行交换,接着从剩下的元素中继续这种选择和交换,最终使序列有序。 //(1)时间复杂度分析: // ①:O(n2) //(2)空间复杂度分析: // ①:O(1):辅助存储空间不随待排序列规模的变化而变化,是个常量。 viod SelectSort(int R[],int n) { int i,j,k; int temp; for(i=0;i<n;++i) { k=i; for(j=i+1;j<n;++j) //该循环从无序序列中挑选出一个最小的元素 if(R[k]>R[j]) k=j; /* 下面3句完成最小元素与无序序列第一个元素的交换 */ temp=R[i]; R[i]=R[k]; R[k]=temp; } }
七、堆排序
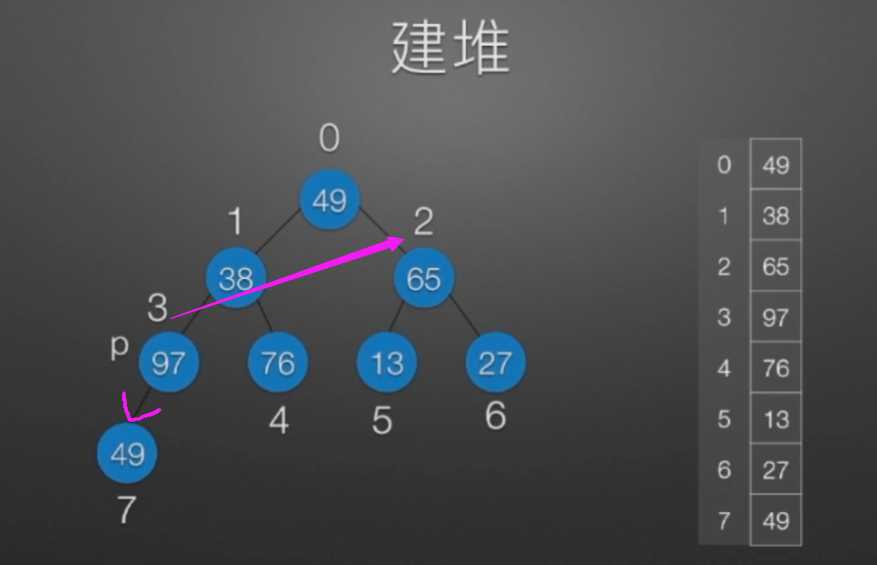
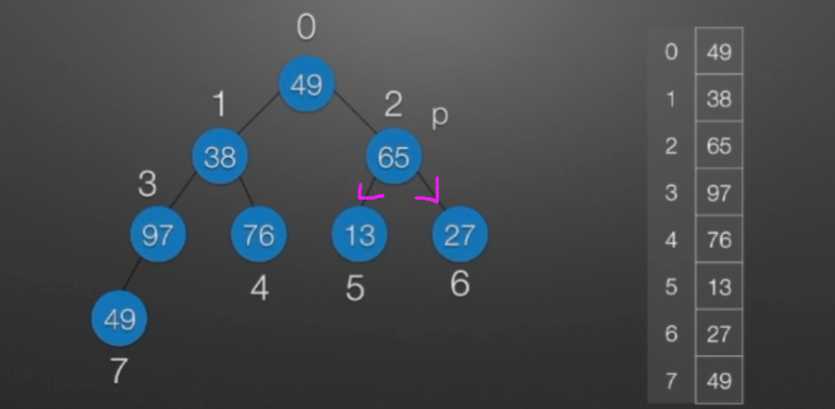
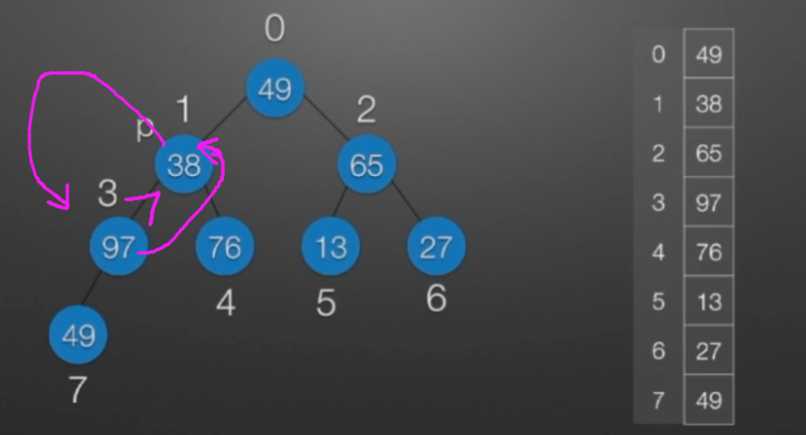
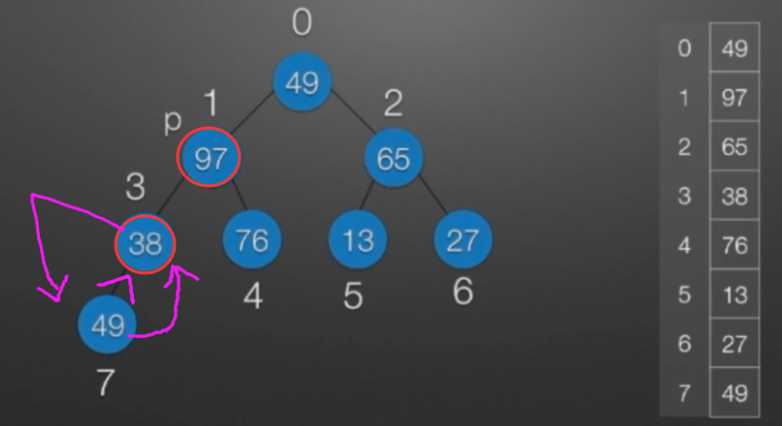
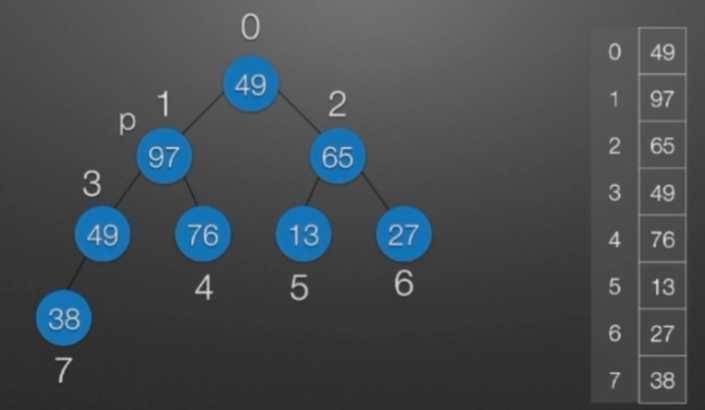
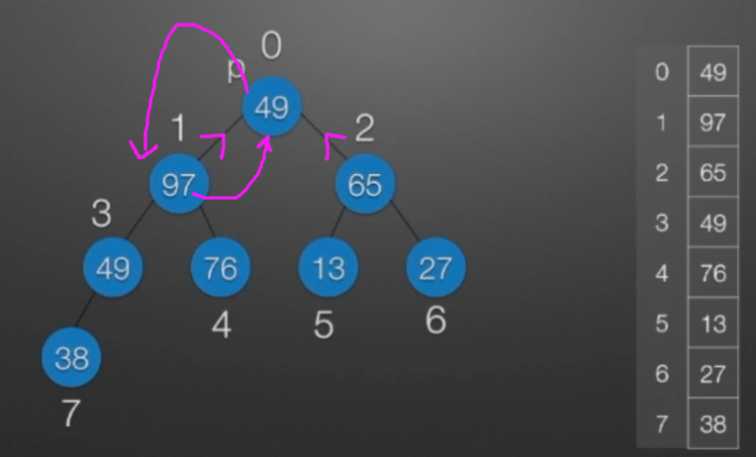
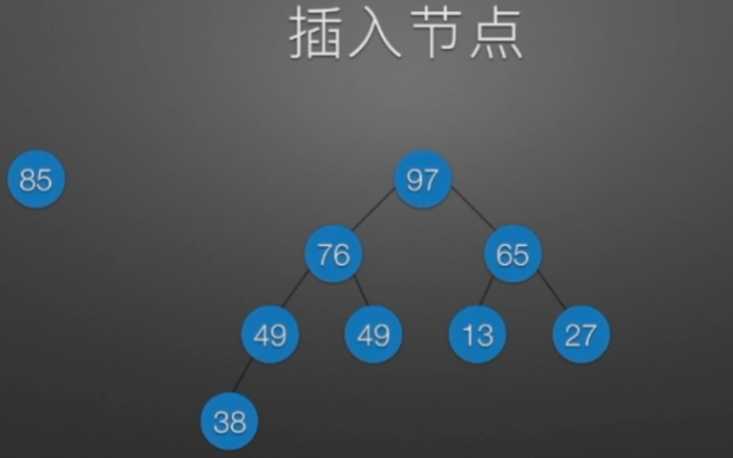
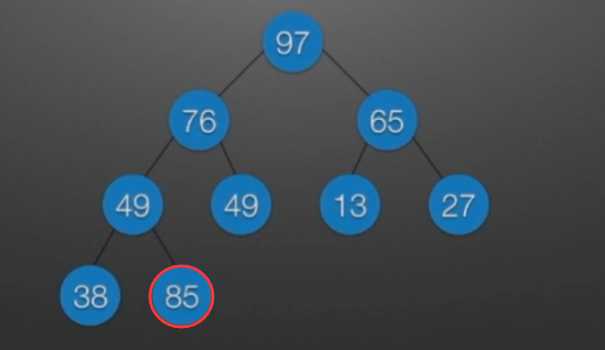
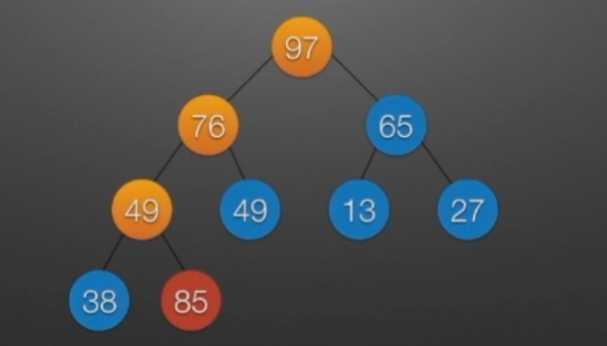
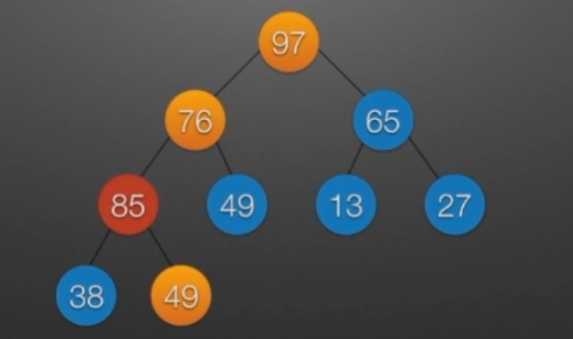
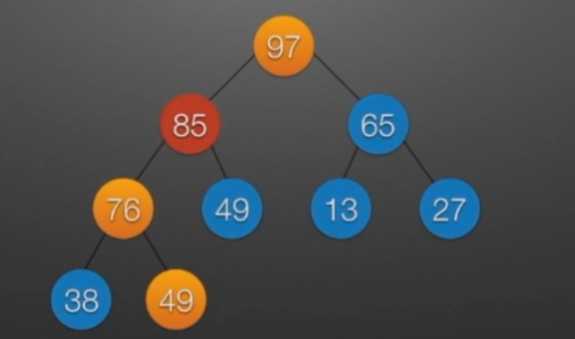
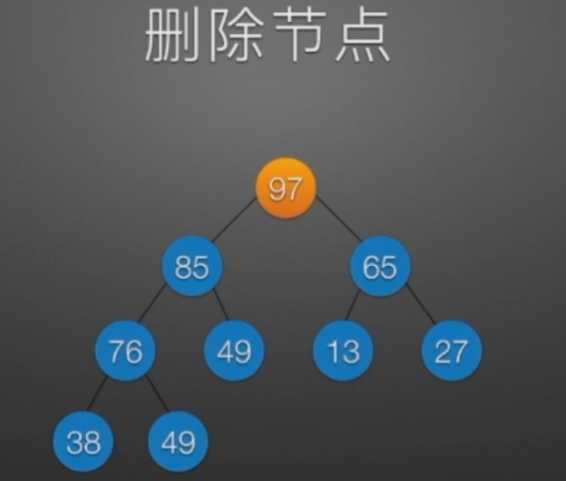
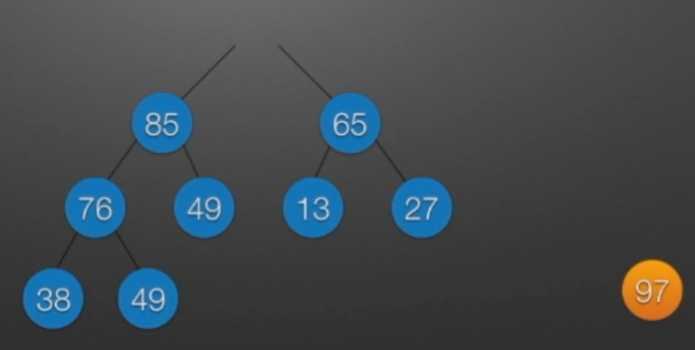
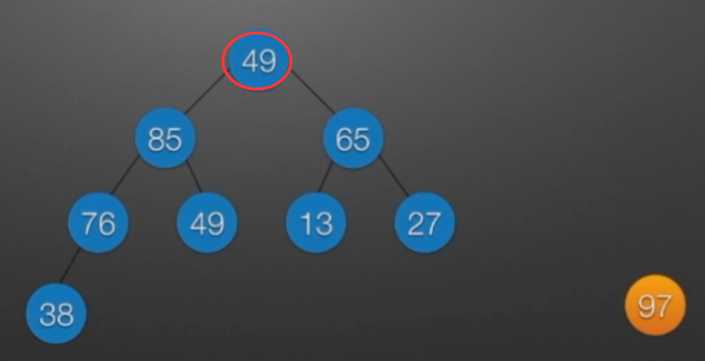
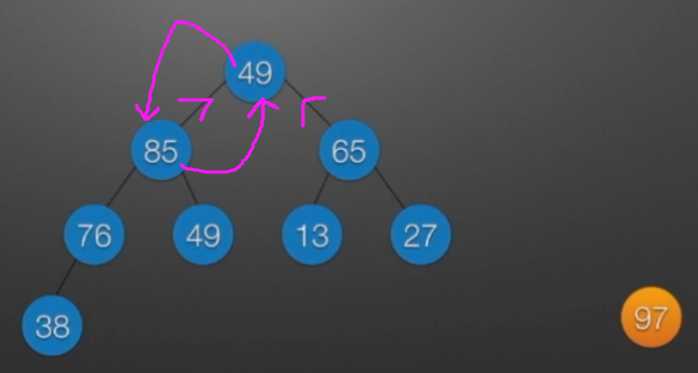
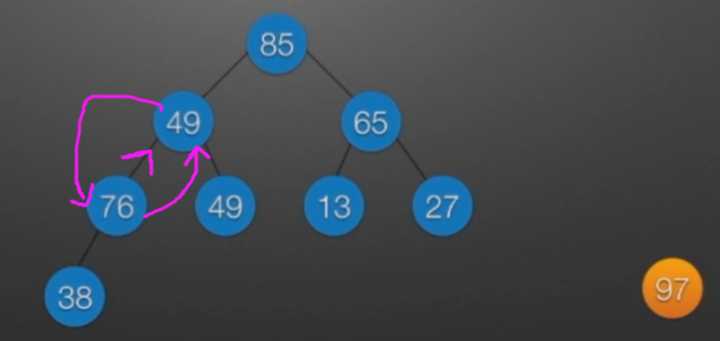
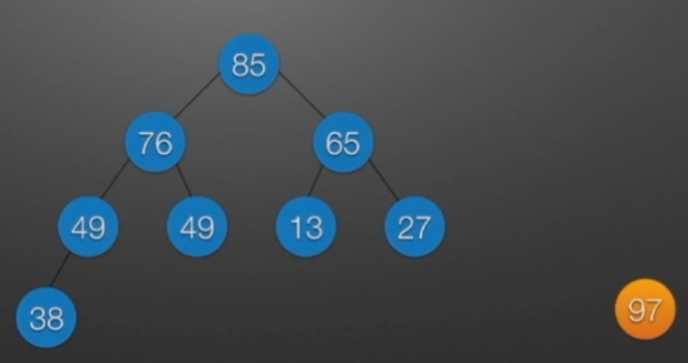
//堆排序 //算法思想: //(1)时间复杂度分析: // ①:O(nlog2?n) //(2)空间复杂度分析: // ①:O(1):辅助存储空间不随待排序列规模的变化而变化,是个常量。 /* 本函数完成在数组R[low]到R[high]范围内,对在位置low上的结点进行调整 */ void Sift(int R[],int low,int high) //R[]中是一棵完全二叉树,所以元素的存储必须从1开始 { int i=low,j=2*i; //R[j]是R[i]的左孩子结点 int temp=R[i]; while(j<=high) { if(j<high && R[j]<R[j+1]) //若右孩子较大,则把j指向右孩子 ++j; //j变为2*i+1 if(temp<R[j]) { R[i]=R[j]; //将R[j]调整到双亲结点的位置上 i=j; //修改i和j的值,以便继续向下调整 j=2*i; } else break; //调整结束 } R[i]=temp; //被调整结点的中放入最终位置 } /* 堆排序函数 */ viod heapSort(int R[],int n) { int i; int temp; for(i=n/2;i>=1;--i) //建立初始堆 Sift(R,i,n); for(i=n;i>=2;--i) //进行n-1次循环,完成堆排序 { /* 以下3句换出了根结点中的元素,将其放入最终位置 */ temp=R[1]; R[1]=R[i]; R[i]=temp; Sift(R,1,i-1); //在减少了1个元素的无序序列中进行调整 } }
八、归并排序
//归并排序 //算法思想: //(1)时间复杂度分析: // ①:O(nlog2?n) //(2)空间复杂度分析: // ①:O(1):辅助存储空间不随待排序列规模的变化而变化,是个常量。 void merge(int arr[],int low,int mid,int high) { int i,j,k; int n1=mid -low+1; int n2=high-mid; int L[n1],R[n2]; for(i=0;i<n1;i++) L[i]=arr[low+i]; for(j=0;j<n2;j++) R[j]=arr[mid+1+j]; i=0; j=0; k=low; while(i<n1 && j<n2) { if(L[i]<=R[j]) arr[k]=L[i++]; else arr[k]=R[j++]; k++; } while(i<n1) arr[k++]=L[i++]; while(j<n2) arr[k++]=R[j++]; } void mergeSort(int arr[],int low,int mid,int high) { if(low<high) { int mid=(low+high)/2; mergeSort(arr,low,mid); //归并排序前半段 mergeSort(a,mid+1,high); //归并排序后半段 merge(A,low,mid,high); //merge()函数:把A数组中low到mid和mid+1到high范围内的两段有序序列归并成一段有序序列 } }
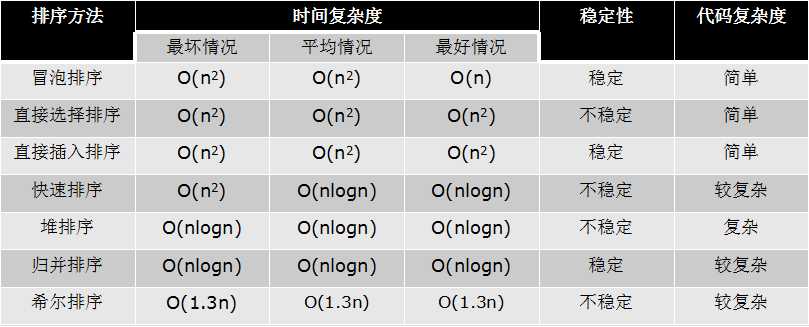
总结对比
快速排序、归并排序 、堆排序三种排序算法的时间复杂度都是O(nlogn)
一般情况下,就运行时间而言:快速排序 < 归并排序 < 堆排序
三种排序算法的缺点:
①快速排序:极端情况下排序效率低
②归并排序:需要额外的内存开销
③堆排序:在快的排序算法中相对较慢
标签:建立 ret 函数 IV 折半插入排序 pre 过多 折半查找 额外
原文地址:https://www.cnblogs.com/liwei1153300111/p/8064115.html