标签:位置 span lsp 小顶堆 获取 var_dump 最大值 nbsp png
图解
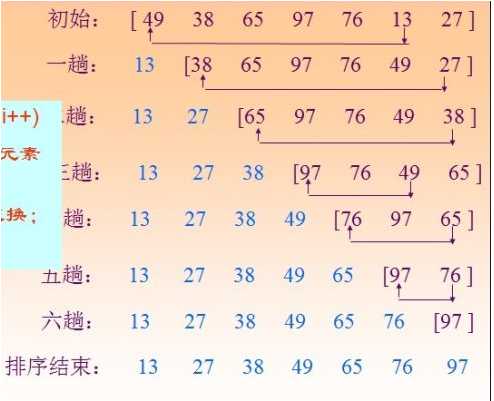
我们可以从图上可以看出,我们先循环找出最小的元素。我们的第二个循环是找出最小的元素,第一个循环是负责交换值的,第一趟排序外层循环的指针指向数组的第一个,这个时候我们找出数组的最小值,和外层指针交换数值,就把最小的放在第一个,后面的同理。
注意:
1、重点在于先循环找出最小的值,再去交换;
<?php
function SelectSort(array &$arr)
{
$length = count($arr);
for($i = 0; $i < $length - 1; $i++){
$min = $i;
for($j = $i+1; $j < $length; $j++){
if( $arr[$min] > $arr[$j]){
$min = $j;
}
}
if($min != $i){
$temp = $arr[$min];
$arr[$min] = $arr[$i];
$arr[$i] = $temp;
}
}
var_dump($arr);
}
$arr = [5,2,6,0,3,9,1,7,4,8];
SelectSort($arr);
| 排序类别 | 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 | ||
| 平均情况 | 最坏情况 | 最好情况 | ||||
| 选择排序类 | 简单选择排序 | O(n2) | O(n2) | O(1) | 稳定 | |
1、什么是大顶堆,和小顶堆?
堆排序是在完全二叉树的结构上建立的。完全二叉树就是每一个父节点都有左孩子和右孩子两个子节点并且他的叶节点是有顺序的,从左到右是连续的;
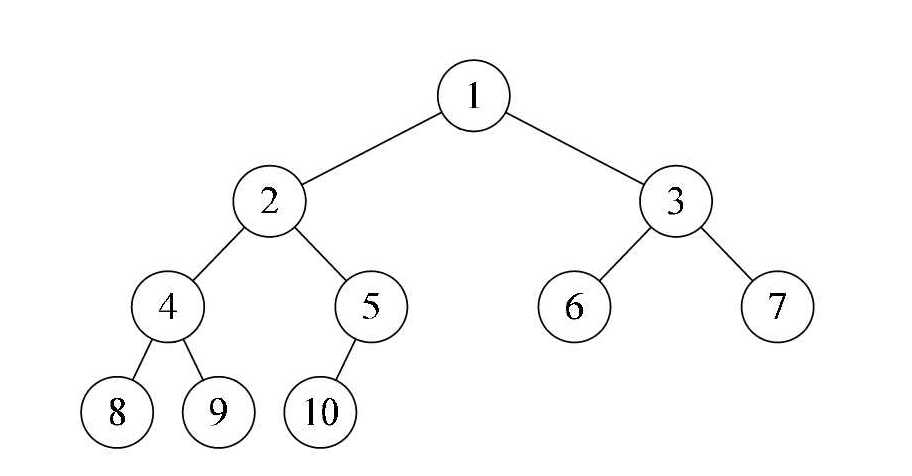
上图就是完全二叉树,大顶堆就是根节点是二叉树里面最大的值并且父节点的值要比两个子节点的值都要大;小顶堆反过来。
2、具体的流程
注意:我以大顶堆为例
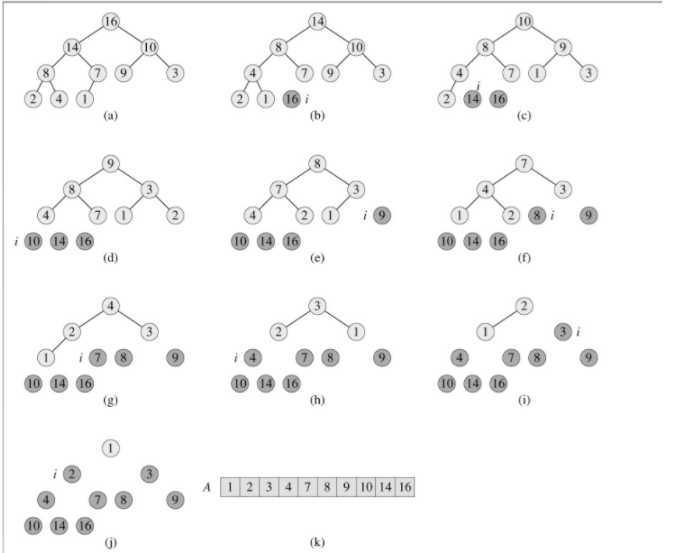
第一步:我们现将目标数组,构建成完全二叉树的结构;
第二步:我们将已经转化后的完全二叉树的根节点和数组最后的一个元素进行互换位置,换完了以后,有可能打破完全二叉树的结构,这时我们再将目标数组构建大顶堆,但是要去掉数组的最大值,也就是数组的长度减1。
3、图解
<?php
/**
*Description:用于两个数之间的交换
*@Param:int a
*@Param:int b
*@Param:array arr
*/
function swap(array &$arr, $a, $b)
{
$temp = $arr[$a];
$arr[$a] = $arr[$b];
$arr[$b] = $temp;
}
/**
*Description:将原数组构建为一个大顶堆
*@Param:int start
*@Param:int end
*@Param:array arr
**/
function HeapAdjest(array &$arr, $start, $end)
{
$temp = $arr[$start];
//左孩子2 * $start + 1,右孩子2 * $start + 2
for($i = 2 * $start + 1; $i <= $end; $i = $i * 2 + 1){
if($i != $end && $arr[$i] < $arr[$i + 1]){
$i++;//转换为右孩子
}
if($temp > $arr[$i]){
break; //满足大顶堆
}
//将根节点设置为子节点较大的值
$arr[$start] = $arr[$i];
$start = $i;
}
$arr[$start] = $temp;
}
/**
*Description:堆排序的主函数
*@Param:array arr
**/
function HeapSort(array &$arr)
{
$len = count($arr);
//先将数组构造成大根堆,由于是完全二叉树,所以这里用floor($count/2)-1
for ($i = floor($len / 2) - 1; $i >= 0; $i--){
HeapAdjest($arr, $i, $len);
}
for ($i = $len - 1; $i >= 0; $i--){
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr, 0, $i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,交换后有可能破坏完全二叉树的结构,继续构建二叉树
HeapAdjest($arr, 0, $i - 1);
}
}
$arr = array(9,1,5,8,3,7,4,6,2);
HeapSort($arr);
var_dump($arr);
注意:
1、在构建大顶堆的时候,我们先要判断左右孩子那个大,在和大的交换位置;
| 排序类别 | 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 | ||
| 平均情况 | 最坏情况 | 最好情况 | ||||
| 选择排序类 | 堆排序 | O(n*log2n) | O(n*log2n) | O(n*log2n) | O(1) | 不稳定 |
标签:位置 span lsp 小顶堆 获取 var_dump 最大值 nbsp png
原文地址:https://www.cnblogs.com/meichao/p/9213278.html