标签:弗洛伊德 zed 距离 ike ber define 算法详解 五行 源代码
对于一个图G=(V, E),求图中两点u, v间最短路径长度,称为图的最短路径问题。最短路径中最长的称为图的直径。
其中,求图中确定的某两点的最短路径算法,称为单源最短路径算法。求图中任意两点间的最短路径算法,称为多源最短路径算法。
其中最经典的是Dijkstra算法和Floyd算法。Floyd算法是多源最短路径算法,可以直接求出图中任意两点间的距离,因此只要取其中最大的就可以得到图的直径。
假设Dis(i,j)为节点u到节点v的最短路径的距离(最短路径长度),对于每一个节点k,检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,说明从i到k再到j的路径比i直接到j的路径短,便记录Dis(i,j) = Dis(i,k) + Dis(k,j)。因此,当遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
在判断Dis(i,k) + Dis(k,j) < Dis(i,j)这个公式时,如果经过k的距离更短就选择k,但是这能否保证此时Dis(i,k)和Dis(k,j)已经取得了最小值呢?
答案是肯定的,可以用数学归纳法证明,参考这篇博客
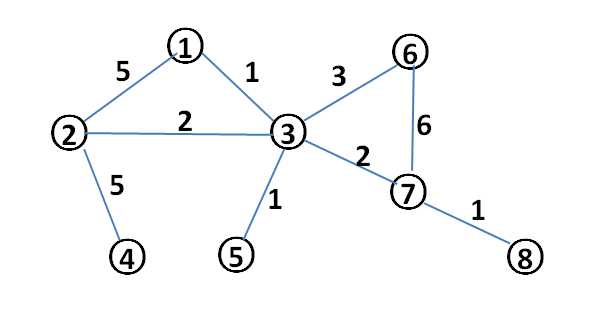
2(表示无向图)
8 9 (表示8个顶点,9条边)
1 2 5 (表示顶点1和顶点2之间的距离权重是5)
... ...
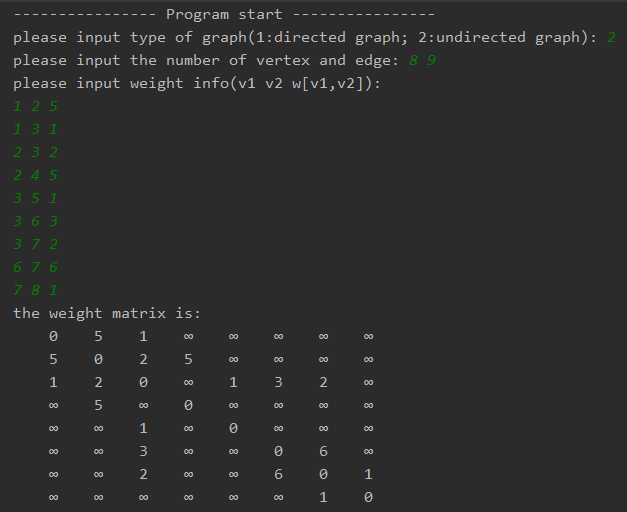
(邻接矩阵,矩阵元素M[i][j]表示顶点Vi与Vj间的距离)
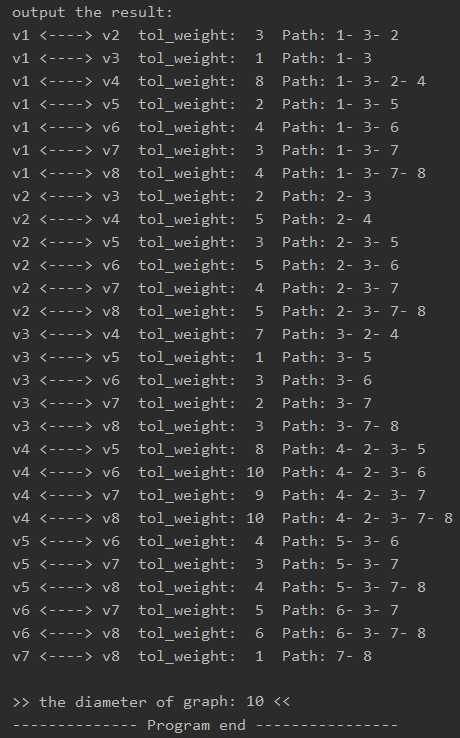
(各个顶点间的最短路径以及路径长度,对于此例,顶点V4与V6或V8间的距离都是10,是距离最远的两个顶点对)
(此图的直径)
# ----------------------------------------------
# Project: calculate diameter of graph
# Using floyd algorithm
# ----------------------------------------------
# define function: print shortest path
def getPath(i, j):
if i != j:
if path[i][j] == -1:
print(‘-‘, j+1, end=‘‘)
else:
getPath(i, path[i][j])
getPath(path[i][j], j)
def printPath(i, j):
print(‘ Path:‘, i+1, end=‘‘)
getPath(i, j)
print()
print(‘---------------- Program start ----------------‘)
# read data
flag = input(‘please input type of graph(1:directed ‘
‘graph; 2:undirected graph): ‘)
vertex, edge = input(‘please input the number of ‘
‘vertex and edge: ‘).strip().split()
# initialized
flag = int(flag)
vertex = int(vertex)
edge = int(edge)
inf = 99999999
dis = [] # matrix of the shortest distance
path = [] # record the shortest path
for i in range(vertex):
dis += [[]]
for j in range(vertex):
if i == j:
dis[i].append(0)
else:
dis[i].append(inf)
for i in range(vertex):
path += [[]]
for j in range(vertex):
path[i].append(-1)
# read weight information
print(‘please input weight info(v1 v2 w[v1,v2]): ‘)
for i in range(edge):
u, v, w = input().strip().split()
u, v, w = int(u)-1, int(v)-1, int(w)
if flag == 1:
dis[u][v] = w
elif flag == 2:
dis[u][v] = w
dis[v][u] = w
print(‘the weight matrix is:‘)
for i in range(vertex):
for j in range(vertex):
if dis[i][j] != inf:
print(‘%5d‘ % dis[i][j], end=‘‘)
else:
print(‘%5s‘ % ‘∞‘, end=‘‘)
print()
# floyd algorithm
for k in range(vertex):
for i in range(vertex):
for j in range(vertex):
if dis[i][j] > dis[i][k] + dis[k][j]:
dis[i][j] = dis[i][k] + dis[k][j]
path[i][j] = k
print(‘===========================================‘)
# output the result
print(‘output the result:‘)
if flag == 1:
for i in range(vertex):
for j in range(vertex):
if (i != j) and (dis[i][j] != inf):
print(‘v%d ----> v%d tol_weight:‘
‘%3d‘ % (i+1, j+1, dis[i][j]))
printPath(i, j)
if (i != j) and (dis[i][j] == inf):
print(‘v%d ----> v%d tol_weight:‘
‘ ∞‘ % (i+1, j+1))
printPath(i, j)
if flag == 2:
for i in range(vertex):
for j in range(i+1, vertex):
print(‘v%d <----> v%d tol_weight:‘
‘%3d‘ % (i+1, j+1, dis[i][j]), ‘‘, end=‘‘)
printPath(i, j)
print()
for i in range(vertex):
for j in range(vertex):
if dis[i][j] == inf:
dis[i][j] = 0
# max(max(dis)): the max item of two dimension matrix
print(‘>> the diameter of graph: %d <<‘ % max(max(dis)))
print(‘-------------- Program end ----------------‘)最短路径_百度百科
最短路径—Dijkstra算法和Floyd算法
最短路径问题---Floyd算法详解 - CSDN博客
Floyd算法(记录路径) - CSDN博客
[Python] 弗洛伊德(Floyd)算法求图的直径并记录路径
标签:弗洛伊德 zed 距离 ike ber define 算法详解 五行 源代码
原文地址:https://www.cnblogs.com/Ran-Chen/p/9219716.html