标签:lin 分割 -- system bottom ott print 期望 create
前文参考:
Python爬虫(三)——对豆瓣图书各模块评论数与评分图形化分析
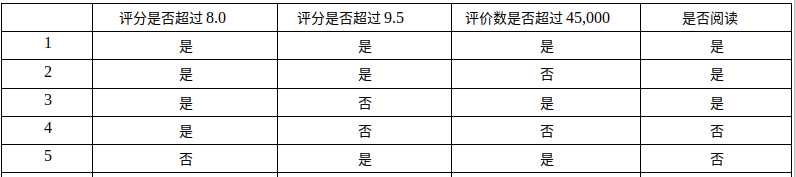
在这张表中我们可以发现这里有5个数据,这里有三个特征(评分是否超过8.0,评分是否超过9.5,评价数是否超过45,000)来划分这5本书是否选择阅读。
现在我们要做的就是是要根据第一个特征,第二个特征还是第三个特征来划分数据,进行分类。
1 def createDataSet(): 2 dataSet = [[1,1,1,‘yes‘], 3 [1,1,0,‘yes‘], 4 [1,0,1,‘yes‘], 5 [1,0,0,‘no‘], 6 [0,1,1,‘no‘]] # 我们定义了一个list来表示我们的数据集,这里的数据对应的是上表中的数据 7 8 labels = [‘no surfacing‘,‘flippers‘] 9 10 return dataSet, labels
根据信息论的方法找到最合适的特征来划分数据集。在这里,我们首先要计算所有类别的所有可能值的香农熵,根据香农熵来我们按照取最大信息增益的方法划分数据集。
以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。信息熵是用来衡量一个随机变量出现的期望值。如果信息的不确定性越大,熵的值也就越大,出现的各种情况也就越多。
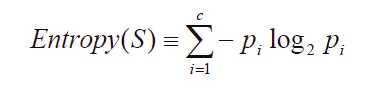
其中,S为所有事件集合,p为发生概率,c为特征总数。注意:熵是以2进制位的个数来度量编码长度的,因此熵的最大值是log2C。
信息增益(information gain)是指信息划分前后的熵的变化,也就是说由于使用这个属性分割样例而导致的期望熵降低。也就是说,信息增益就是原有信息熵与属性划分后信息熵(需要对划分后的信息熵取期望值)的差值,具体计算法如下:
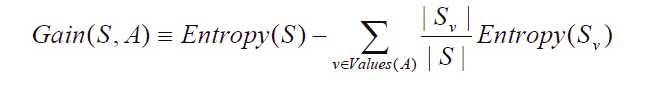
代码实现:
1 from math import log 2 3 def calcShannonEnt(dataSet):#传入数据集 4 # 在这里dataSet是一个链表形式的的数据集 5 countDataSet = len(dataSet) 6 labelCounts={} # 构建字典,用键值对的关系我们表示出 我们数据集中的类别还有对应的关系 7 for featVec in dataSet: 通过for循环,我们每次取出一个数据集,如featVec=[1,1,‘yes‘] 8 currentLabel=featVec[-1] # 取出最后一列 也就是类别的那一类,比如说‘yes’或者是‘no’ 9 if currentLabel not in labelCounts.keys(): 10 labelCounts[currentLabel] = 0 11 labelCounts[currentLabel] += 1 12 13 print labelCounts 14 15 shang = 0.0 16 17 for key in labelCounts: 18 prob = float(labelCounts[key])/countDataSet 19 shang -= prob * log(prob,2) 20 return shang
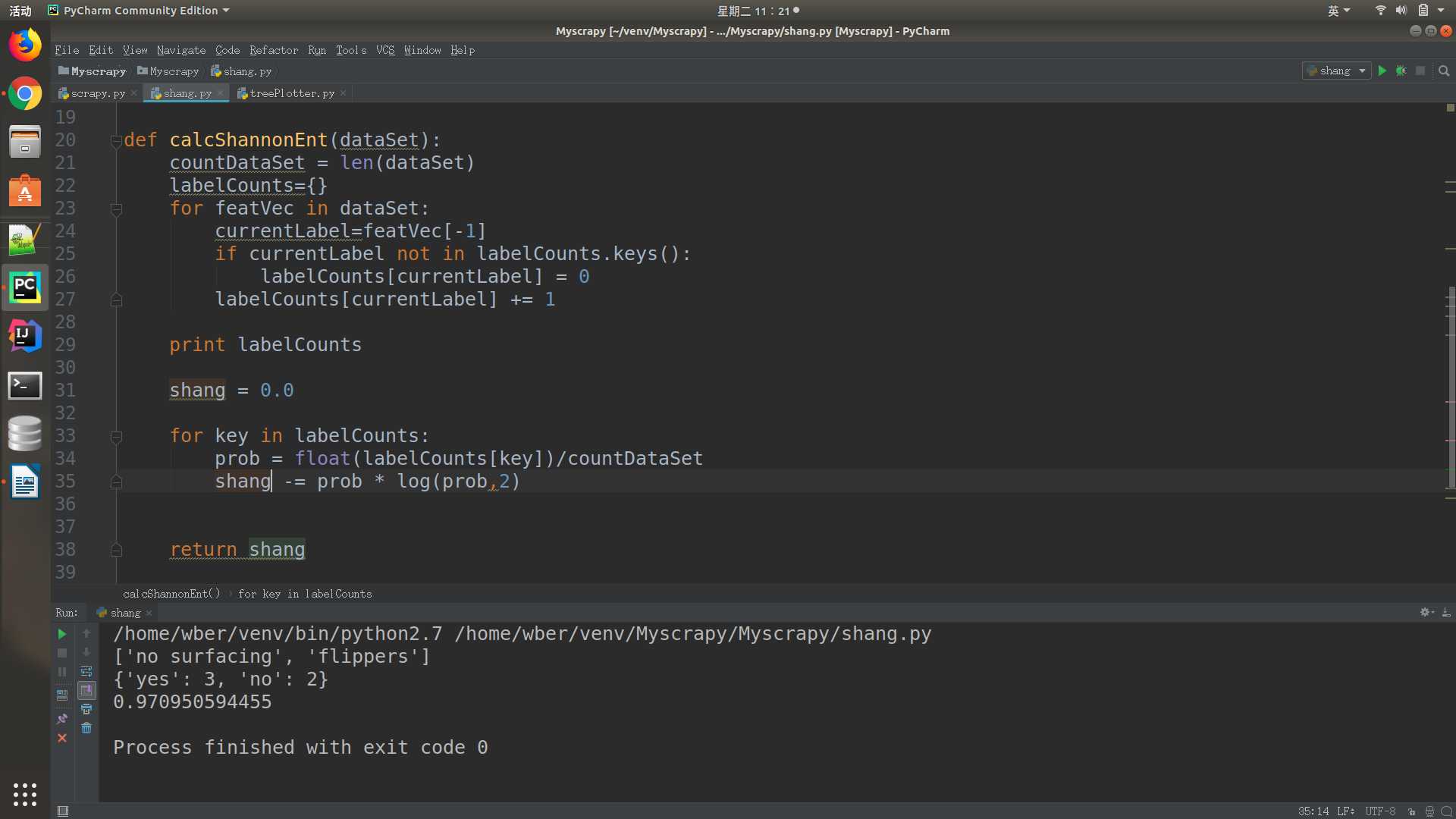
在度量数据集的无序程度的时候,分类算法除了需要测量信息熵,还需要划分数据集,度量花费数据集的熵,以便判断当前是否正确的划分了数据集。
我们将对每个特征数据集划分的结果计算一次信息熵,然后判断按照那个特征划分数据集是最好的划分方式。
也就是说,我们依次选取我们数据集当中的所有特征作为我们划定的特征,然后计算选取该特征时的信息增益,当信息增益最大时我们就选取对应信息增益最大的特征作为我们分类的最佳特征。

1 dataSet = [[1, 1, 1, ‘yes‘], 2 [1, 1, 0, ‘yes‘], 3 [1, 0, 1, ‘yes‘], 4 [1, 0, 0, ‘no‘], 5 [0, 1, 1, ‘no‘]]
在这个数据集当中有三个特征,就是每个样本的第一列,第二列和第三列,最后一列是它们所属的分类。
我们划分数据集是为了计算根据那个特征我们可以得到最大的信息增益,那么根据这个特征来划分数据就是最好的分类方法。
因此我们需要遍历每一个特征,然后计算按照这种划分方式得出的信息增益。信息增益是指数据集在划分数据前后信息的变化量。
标签:lin 分割 -- system bottom ott print 期望 create
原文地址:https://www.cnblogs.com/LexMoon/p/douban4.html