标签:package 介绍 com oid node 左右 数据结构 显示 img
二叉树是我们在程序中用的最多的一种树(个人观点)。最简单的一个二叉树是由一个根节点,两个子节点(一左一右成左右孩子节点)组成。二叉树是数组和链表的结合,即包含了数组的快速查找优点,又包含了链表的快速添加删除的优点。熟练掌握二叉树的遍历方法是很有必要的。下面来介绍一下基于二叉树的四种遍历方式。
下面我们以一个棵简单的二叉树为例来说明四种遍历:
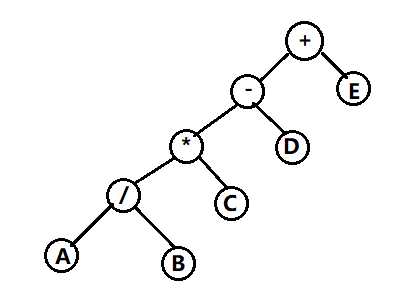
创建树节点类:
//树节点 class TreeNode { public char val; public TreeNode left; public TreeNode right; public TreeNode(char x) { val = x; } }
中序遍历:
先遍历左孩子节点---根节点---右孩子节点
//中序遍历 左-根-右 (前中后:根的位置) public void InOrder(TreeNode current){ if(current != null) { InOrder(current.left); Visit(current); InOrder(current.right); } }
前序遍历:
遍历根节点---左孩子节点---右孩子节点
//前序遍历 根-左-右 public void PreOrder(TreeNode current){ if(current != null) { Visit(current); InOrder(current.left); InOrder(current.right); } }
后序遍历:
遍历左孩子节点---右孩子节点---根节点
//后续遍历 左-右-根 public void PostOrder(TreeNode current){ if(current != null) { InOrder(current.left); InOrder(current.right); Visit(current); } }
层序遍历:
同一层节点从左往右依次遍历。
//层序遍历 同一层节点从左往右依次遍历 FIFO public void LevelOrder(TreeNode current){ List<TreeNode> q = new ArrayList<TreeNode>(); while(current != null) { Visit(current); if(current.left != null) { q.add(current.left); } if(current.right != null) { q.add(current.right); } if(q.isEmpty()) return ; current = q.remove(0); } }
以上就是四种基本遍历方式。下面我们来测试一下,首先写一个工具函数,用来显示当前节点的值。
//*********辅助工具**************** public void Visit(TreeNode node) { System.out.print(node.val); }
写Test测试函数:
@Test public void fun() { TreeNode root = new TreeNode(‘+‘); root.left = new TreeNode(‘-‘); root.right = new TreeNode(‘E‘); root.left.left = new TreeNode(‘*‘); root.left.right = new TreeNode(‘D‘); root.left.left.left = new TreeNode(‘/‘); root.left.left.right = new TreeNode(‘C‘); root.left.left.left.left = new TreeNode(‘A‘); root.left.left.left.right = new TreeNode(‘B‘); System.out.println("中序遍历:"); InOrder(root); System.out.println(); System.out.println("前序遍历:"); PreOrder(root); System.out.println(); System.out.println("后序遍历:"); PostOrder(root); System.out.println(); System.out.println("层序遍历:"); LevelOrder(root); System.out.println(); }
由上面的测试函数得到遍历结果:
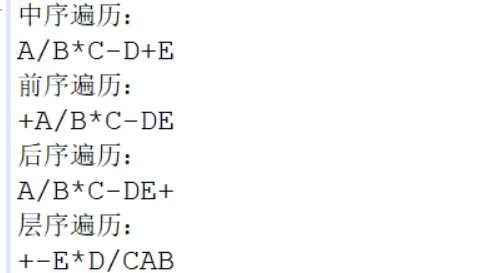
全部代码:
package tree; import java.util.ArrayList; import java.util.List; import org.junit.Test; /** * 二叉数的遍历 * + * - E * * D * / C * A B * @author Ranter * */ public class BinaryTree { @Test public void fun() { TreeNode root = new TreeNode(‘+‘); root.left = new TreeNode(‘-‘); root.right = new TreeNode(‘E‘); root.left.left = new TreeNode(‘*‘); root.left.right = new TreeNode(‘D‘); root.left.left.left = new TreeNode(‘/‘); root.left.left.right = new TreeNode(‘C‘); root.left.left.left.left = new TreeNode(‘A‘); root.left.left.left.right = new TreeNode(‘B‘); System.out.println("中序遍历:"); InOrder(root); System.out.println(); System.out.println("前序遍历:"); PreOrder(root); System.out.println(); System.out.println("后序遍历:"); PostOrder(root); System.out.println(); System.out.println("层序遍历:"); LevelOrder(root); System.out.println(); } //**************************************************************** //中序遍历 左-根-右 (前中后:根的位置) public void InOrder(TreeNode current){ if(current != null) { InOrder(current.left); Visit(current); InOrder(current.right); } } //前序遍历 根-左-右 public void PreOrder(TreeNode current){ if(current != null) { Visit(current); InOrder(current.left); InOrder(current.right); } } //后续遍历 左-右-根 public void PostOrder(TreeNode current){ if(current != null) { InOrder(current.left); InOrder(current.right); Visit(current); } } //层序遍历 同一层节点从左往右依次遍历(使用队列层序遍历) public void LevelOrder(TreeNode current){ List<TreeNode> q = new ArrayList<TreeNode>(); while(current != null) { Visit(current); if(current.left != null) { q.add(current.left); } if(current.right != null) { q.add(current.right); } if(q.isEmpty()) return ; current = q.remove(0); } } //*********辅助工具**************** public void Visit(TreeNode node) { System.out.print(node.val); } //树节点 class TreeNode { public char val; public TreeNode left; public TreeNode right; public TreeNode(char x) { val = x; } } }
标签:package 介绍 com oid node 左右 数据结构 显示 img
原文地址:https://www.cnblogs.com/ranter/p/9229809.html