标签:selected plot 目的 图片 setup span sort 情况下 算法
一、前言
1、在给定WSN的节点数目(100)前提下,节点随机分布,按照LEACH算法,实现每一轮对WSN的分簇。记录前K轮(k=10)时,网络的分簇情况,即每个节点的角色(簇头或簇成员)。标记节点之间的关系,标记其所属的簇头。
2、在1的基础上,增加能量有效性控制:给定的所有节点具有相同的能量,考察第一个节点能量耗尽出现在第几轮。节点的能量消耗仅考虑关键的几次通信过程,其他能量消耗不计。通信过程能量消耗规则如下:
Setup:簇成元:每次收到候选簇头信息-1,每个候选簇头仅被收集一次;通知簇头成为其成员,发送信息-2。候选簇头:被簇成元接收信息,即发送信息,能量-2;被通知成为簇头,接收信息能量-1。
Steady:每个簇成员每轮向簇头发送10次数据,每次成员能量-2,簇头能量-1。
二、目的
(1)在固定节点个数的前提下,仿真LEACH算法的分簇过程。
(2)在上述节点个数和分簇算法的前提下,计算节点的能量消耗,判断能量消耗到0的节点出现在第几轮。
三、方法描述
(1)LEACH分簇
簇头选举初始阶段,每个节点根据所建议网络簇头的百分比(事先确定)和节点已经成为簇头的次数来确定自己是否当选为簇头。每个节点产生一个0-1的随机数字,如果该数字小于阈值,节点成为当前轮的簇头。阈值
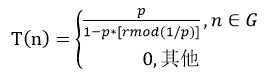
其中,P为预期的簇头百分比,r为当前轮数,G是最近1/p轮里没有成为簇头的节点的集合。
首先确定传感器网络中的节点个数为100个,并对所有节点初始化其三个属性,分别有type(节点类型),selected(是否当选过簇头)和temp_rand(随机数)。设定簇头产生概率p=0.08。
算法步骤如下:
Step1:随机生成100个节点位置,并赋值随机数temp_rand,设置type和selected为’N’。
Step2:将所有selected为’N’的节点随机值与做比较,若temp_rand小于等于则转向Step3,否则转向Step4。
Step3:表明节点当选为簇头节点,将type赋值’C’, selected赋值’O’。
Step4:表明节点为普通节点,将type扔赋值’N’, selected不改变赋值。
Step5:遍历所有节点,若节点type为’C’,将节点在图上标记’*’,并标上节点数目。否则将节点在图上标记为’o’,同时标记上节点数目。
Step6:如果节点为普通节点,则计算其与所有簇头的欧式距离,形成距离矩阵。
Step7:利用min函数,找到与普通节点相距最近的簇头,并将其相连接。
Step8:一轮分簇结束,返回Step1开始下一轮分簇过程。
所以在试验中通过计算每个普通节点到所有簇头的距离,并将该普通节点与相距最近的簇头节点相连,并将簇头节点的selected属性标记,保证当过簇头的节点在之后的分簇过程中不会再当选为簇头节点。在10轮的分簇试验中选取4张分簇网络图,具体分簇情况分别如下:
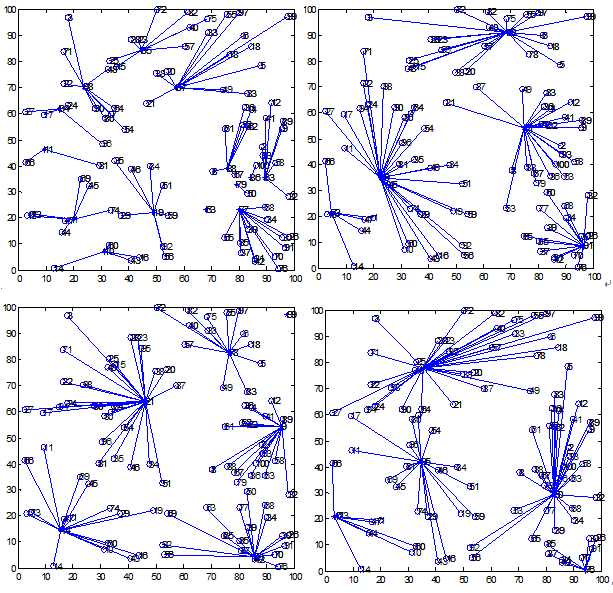
(2)节点能量消耗
试验中通过对能量消耗规律的分析可以得出:假设某轮分簇中第i个簇头的簇成员有a个,所以在这一轮中的通信过程中簇头消耗的能量为2+11*a,簇成员消耗的能量为22。所以增加节点的一个属性为S(i).power,从而到达能量消耗监测的目的。设置标志位,当发现第一个节点能量耗尽情况出现时,则结束程序,并用黑色标记。而已做过簇头的节点用红色标记。
在一次实验中,第一次能量耗尽出现在第5轮。前5轮的图像如下:
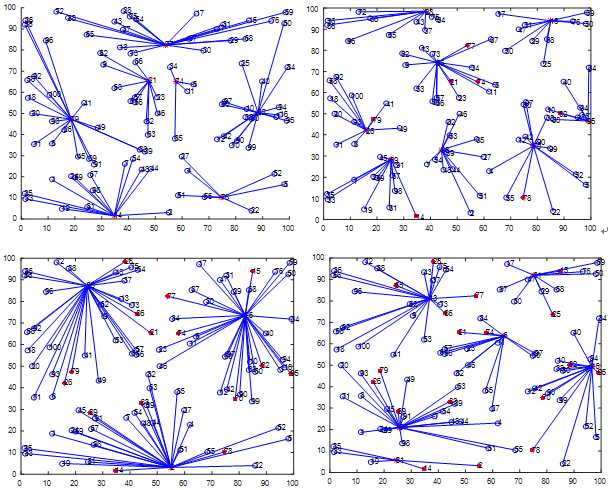
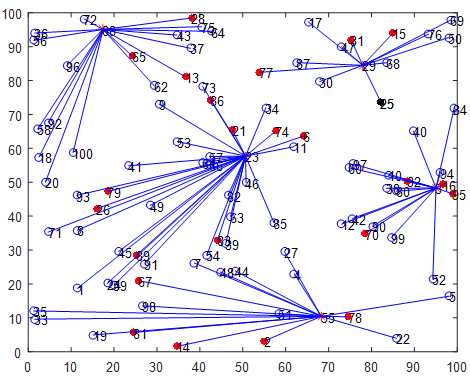 三、结论
三、结论
在本次实验中首先通过对LEACH算法的分析研究,学习了其进行传感器节点网络分簇的步骤,同时在P=0.08和节点数目为100的前提下通过MATLAB仿真在节点数目不变的情况下10轮的分簇结果。在能量的消耗试验中,首先通过对簇头以及簇成员在一轮分簇通信过程中的能量消耗规律统计,简化了实验步骤。通过仿真,第一个节点能量耗尽的情况出现在第5轮。
四、程序代码
(1)Leach分簇:
close all clear all; clc; pm=100; %概率范围 xm=100; %x轴范围 ym=100; %y轴范围 line=10; %连线距离初始值 sink.x=0.5*xm; %基站x轴 50 sink.y=0.5*ym; %基站y轴 50 n=100; p=0.08; for i=1:1:n %随机产生100个点 S(i).xd=rand(1,1)*xm; S(i).yd=rand(1,1)*ym; S(i).temp_rand=rand; S(i).type=‘N‘; %进行选举簇头前先将所有节点设为普通节点 S(i).selected=‘N‘; S(i).power=300; hold on; end num11=0; num12=0; flag=1; while(flag) for r=1:1:10 figure(r); for i=1:1:n %随机产生100个点 S(i).temp_rand=rand; end for i=1:1:n if S(i).selected==‘N‘ %if S(i).type==‘N‘ %只对普通节点进行选举,即已经当选簇头的节点不进行再选举 if ( S(i).temp_rand<=(p/(1-p*mod(r,round(1/p))))) S(i).type=‘C‘; %节点类型为蔟头 S(i).selected=‘O‘; plot(S(i).xd,S(i).yd,‘*‘); text(S(i).xd,S(i).yd,num2str(i)); num11=num11+1; else S(i).type=‘N‘; %节点类型为普通 plot(S(i).xd,S(i).yd,‘o‘); text(S(i).xd,S(i).yd,num2str(i)); num12=num12+1; end end if S(i).type==‘C‘ plot(S(i).xd,S(i).yd,‘*‘); %蔟头节点以*标记 text(S(i).xd,S(i).yd,num2str(i)); else plot(S(i).xd,S(i).yd,‘o‘); %普通节点以o标记 text(S(i).xd,S(i).yd,num2str(i)); end hold on; end %判断最近的簇头结点,如何去判断,采用距离矩阵 yy=zeros(n); for a=1:1:n if S(a).type==‘N‘ for b=1:1:n if S(b).type==‘C‘ length(a,b)=sqrt((S(a).xd-S(b).xd)^2+(S(a).yd-S(b).yd)^2); %簇头与每个普通节点的距离 else length(a,b)=10000; end end [val,b]=min(length(a,:)); plot([S(b).xd;S(a).xd],[S(b).yd;S(a).yd]) %将节点与簇头连起来,即加入簇头集合 yy(a,b)=1; hold on else length(a,:)=10000; end end for i=1:1:n if S(i).type==‘C‘ number=sum(yy(:,i)) S(i).power=S(i).power-(2+11*number); else S(i).power=S(i).power-22; end end for i=1:1:n S(i).type=‘N‘; end end for i=1:1:n if (S(i).power)<0 text(S(i).xd,S(i).yd,num2str(i)); flag=0; end end if flag==0 break end end
(2)能量
clear clc close all xm=100; ym=100; line=10; sink.x=0.5*xm; sink.y=0.5*ym; n=100; p=0.05; send_dissipation=2; receive_dissipation=1; for i=1:1:n S(i).xd=rand(1,1)*xm; S(i).yd=rand(1,1)*ym; S(i).temp_rand=rand; S(i).energy=500; S(i).signal=‘L‘; S(i).type=‘N‘; S(i).selected=‘N‘; hold on; end r=1; flag=1; while(flag) for i=1:n if S(i).selected==‘N‘&(S(i).temp_rand<=(p/(1-p*mod(r,round(1/p)))))&S(i).signal==‘L‘ flag=1; break; end if i==n if S(i).selected==‘Y‘|(S(i).temp_rand>=(p/(1-p*mod(r,round(1/p)))))|S(i).signal==‘D‘ flag=0; end end end if flag==0 break; end figure(r); for i=1:n if S(i).signal==‘L‘ if S(i).selected==‘N‘ if ( S(i).temp_rand<=(p/(1-p*mod(r,round(1/p))))) S(i).type=‘C‘; S(i).selected=‘Y‘; S(i).energy=S(i).energy-send_dissipation; plot(S(i).xd,S(i).yd,‘r*‘); text(S(i).xd,S(i).yd,num2str(i)); else S(i).type=‘N‘; plot(S(i).xd,S(i).yd,‘bo‘); text(S(i).xd,S(i).yd,num2str(i)); end else plot(S(i).xd,S(i).yd,‘r.‘,‘markersize‘,20); text(S(i).xd,S(i).yd,num2str(i)); end hold on; end end distance=zeros(1,100); num_cluster=zeros(1,100); for i=1:100 distance(1,i)=100000; end for a=1:1:n if S(a).signal==‘L‘&S(a).type==‘N‘ for b=1:1:n if S(b).signal==‘L‘&S(b).type==‘C‘ distance(1,b)=sqrt((S(a).xd-S(b).xd)^2+(S(a).yd-S(b).yd)^2); S(a).energy=S(a).energy-receive_dissipation; end end min=100000; for i=1:n if distance(1,i)<min; min=distance(1,i); nearest_cluster=i; end end if min~=100000; plot([S(nearest_cluster).xd;S(a).xd],[S(nearest_cluster).yd;S(a).yd],‘b‘); hold on; S(a).energy=S(a).energy-send_dissipation; S(nearest_cluster).energy=S(nearest_cluster).energy-receive_dissipation; S(a).energy=S(a).energy-10*send_dissipation; S(nearest_cluster).energy=S(nearest_cluster).energy-10*receive_dissipation; end end end energy=zeros(1,100); energy1=zeros(1,100); for i=1:n energy(1,i)=S(i).energy; end energy1=sort(energy); for i=1:n if S(i).energy<=0 S(i).signal=‘D‘; plot(S(i).xd,S(i).yd,‘k.‘,‘markersize‘,20); text(S(i).xd,S(i).yd,num2str(i)); hold on; end end for i=1:n S(i).type=‘N‘; if S(i).selected==‘N‘ S(i).temp_rand=rand; end end r=r+1; end
君子有三畏:畏天命,畏大人,畏圣人之言。小人不知天命而不畏也,狎大人,侮圣人之言。
转载需说明出处,笔者总结之前的知识,与大家分享,有问题的可以留给我哦~
标签:selected plot 目的 图片 setup span sort 情况下 算法
原文地址:https://www.cnblogs.com/lemonzhang/p/9254435.html